حل نظام من معادلتين خطيتين بالتعويض
حل أسئلة أتحقق من فهمي :
أتحقق من فهمي :
أحل كلاً من أنظمة المعادلات الاتية مستعملاً التعويض:
1) y = 17 - 4x
2x + y = 9
المعادلة الثانية :
2x + y = 9 المعادلة الثانية
2x + ( 17 - 4x ) = 9 أعوض ب
2x + 17 - 4x = 9
x = 4
أعوض بدلاً من y في المعادلة الاولى
y = 17 - 4x
y = 17 - 4 ( )
y = 17 - 16
y = 1
إذن حل النظام هو ( 1 , 4 )
........................................................................................................................................................................................................................................................................
2) y - 5x = 1
x = y + 3
أعوض بدلاً من x في المعادلة الأولى
y - 5x = 1 المعادلة الأولى
y - 5 ( y + 3 ) = 1
y - 5y + 15 = 1
- 4y = 16
y = -4
أعوض 4 - بدلاً من y في المعادلة الثانية :
x = y + 3 المعادلة الثانية
x = -4 + 3
x = - 1
إذن حل النظام ( 4 - , 1 - )
...................................................................................................................................................................................................................................................................
أتحقق من فهمي :
أحل كلاً من أنظمة المعادلات الآتية مستعملاً التعويض:
1) 4x + 3y = 37
2x + y = 17
من المعادلة الثانية أعزل y فيكون :
2x + y = 17 المعادلة الثانية
2x + y - 2x = 17 - 2x
y = 17 - 2x
أعوض بدلاً من y في المعادلة الأولى :
4x + 3y = 37 المعادلة الأولى
4x + 3 ( 17 - 2x ) = 37
4x + 51 - 6x = 37
x = 7
أعوض 7 بدلاً من y في المعادلة الثانية :
2 ( 7 ) + y = 17
14 + y = 17
14 + y - 14 = 17 - 14
y = 3
إذن حل النظام ( 3 , 7 )
.....................................................................................................................................................................................................................................................................
2) x + 3y = 7
2x - y = 7
أعزل x من المعادلة الأولى :
x + 3y = 7
x + 3y - 3y = 7 - 3y
x = 7 - 3y
أعوض بدلاً من x في المعادلة الثانية :
2x - y = 7
2 ( 7 - 3y ) - y = 7
14 - 6y -y = 7
14 - 7y = 7
14 - 7y - 14 = 7 - 14
y = 1
أعوض 1 بدلاً من y في المعادلة الثانية :
2x - y = 7
2x - 1 = 7
2x - 1 + 1 = 7 + 1
2x = 8
x = 4
إذن حل النظام ( 1 , 4 )
....................................................................................................................................................................................................................................................................
أتحقق من فهمي :
أحل نظام كلاً من المعادلات الآتية مستعملاً التعويض :
3) x - 2y = 4
8y - 4x = 8
أعزل x من المعادلة الأولى
x - 2y = 4
x - 2y + 2y = 4 + 2y
x = 4 + 2y
أعوض بدلاً من x في المعادلة الثانية :
8y - 4x = 8
8y - 4 ( 4 + 2y ) = 8
8y - 16 - 8y = 8
الجملة الأخيرة خاطئة
إذن لا يوجد حل لنظام المعادلتين.
....................................................................................................................................................................................................................................................................
4) x - 5y = 15
10 y - 2x = - 30
أعزل x من المعادلة الأولى
x - 5y = 15
x - 5y + 5y = 15 + 5y
x = 15 + 5y
أعوض بدلاً من x في المعادلة الثانية :
10y - 2x = - 30
10 y - 2 ( 15 + 5y ) = - 30
10y - 30 - 10y = - 30
الجملة الأخيرة صحيحة
إذن يوجد عدد لا نهائي من الحلول
............................................................................................................................................................................................................................................................
أتحقق من فهمي :
اشترى خالد كتابا وناقلة بيانات ب 14 دينار، اذا كان مثلا ثمن الكتاب يزيد عن ثمن ناقلة البيانات بمقدار 10 دنانير،
فما سعر كل من ناقلة البيانات والكتاب؟
الحل :
المعطيات : - ثمن الكتاب وناقلة البيانات 14 دينار
- مثلا ثمن الكتاب يزيد عن ثمن ناقلة البيانات بمقدار 10 دنانير
المطلوب : سعر كل من ناقلة البيانات والكتاب
المتغيرات : x : سعر ناقلة البيانات
y : سعر الكتاب
المعادلات :
x + y = 14
2y- x = 10
أحل نظام المعادلتين الخطيتين :
أعزل x من المعادلة الاولى :
x = 14 - y
اعوض ( ) بدلاً من x في المعادلة الثانية :
2 y - ( 14 - y ) = 10
2y - 14 + y = 10
3y - 14 = 10
3y = 10 + 14
3y = 24
y = 8
أعوض 8 بدلاً من y في المعادلة الاولى:
x + y = 14
x + 8 = 14
x = 14 - 8
x = 6
إذن ثمن ناقلة البيانات هو 6 دينار ، وثمن الكتاب هو 8 دنانير
....................................................................................................................................................................................................................................................................
حل أسئلة وتمارين الكتاب :
أتدرب وأحل المسائل :
أحل كلاً من أنظمة المعادلات الآتية مستعملاً بالتعويض :
1) y = 4x + 2
2x + y = 8
أعوض قيمة y من المعادلة الأولى في المعادلة الثانية:
2x + y = 8 المعادلة الثانية
2x + ( 4x + 2 ) = 8
2x + 4x + 2 = 8
6x + 2 = 8
6x + 2 - 2 = 8 - 2
6x = 6
x = 1
أعوض x = 1 في المعادلة الأولى :
y = 4x + 2 المعادلة الأولى
y = 4 ( 1 ) + 2
y = 4 + 2
y = 6
إذن حل النظام ( 6 , 1 )
....................................................................................................................................................................................................................................................................
2) y = x + 5
y = - 2x - 4
أعوض قيمة y من المعادلة الاولى في المعادلة الثانية
y = - 2x - 4
x + 5 = - 2x - 4
x + 5 + 2x = - 2x - 4 + 2x
3x + 5 = - 4
3x + 5 - 5 = - 4 -5
3x = - 9
x = - 3
أعوض x = -3 في المعادلة الأولى :
y = -3 + 5
y = + 2
إذن حل النظام هو ( 2 , 3- )
......................................................................................................................................................................................................................................................................
3)
أعوض قيمة x من المعادلة الأولى في المعادلة الثانية :
أعوض y = 4 في المعادلة الأولى :
إذن حل النظام هو ( 4 , 1 )
............................................................................................................................................................................................................................................................................
4)
y = 9 - 5x
أعوض قيمة y من المعادلة الثانية في المعادلة الأولى :
أعوض x = 2 في المعادلة الثانية :
y = 9 - 5 x
y = 9 - 5 ( 2 )
y = 9 - 10
y = -1
إذن حل النظام هو ( 1- , 2 )
...................................................................................................................................................................................................................................................................
5) x - 4y = 20
y - 3x = 6
أعزل x من المعادلة الأولى
x - 4y = 20
x - 4y + 4y = 20 + 4y
x = 20 + 4y
أعوض في المعادلة الثانية
y - 3x = 6
y - 3 ( 20 + 4y ) = 6
y - 60 - 12y = 6
y = - 6
أعوض قيمة y في المعادلة الأولى
x - 4y = 20
x - 4 (- 6 ) = 20
x + 24 = 20
x + 24 - 24 = 20 - 24
x = - 4
إذن حل النظام ( 6 - , 4 - )
...................................................................................................................................................................................................................................................................
6) y - 6x = 3
y - 2x = 3
أعزل y من المعادلة الأولى :
y - 6x = 3
y - 6x + 6x = 3 + 6x
y = 3 + 6x
أعوض في المعادلة الثانية :
y - 2x = 3
( 3 + 6x ) - 2x = 3
3 + 6x - 2x = 3
3 + 4x = 3
3 + 4x - 3 = 3 - 3
4x = 0
x = 0
أعوض x = 0 في المعادلة الاولى
y - 6x = 3
y - 6 ( 0 ) = 3
y - 0 = 3
y = 3
إذن حل النظام هو ( 3 , 0 )
.......................................................................................................................................................................................................................................................................
7) 8x - y = 16
أعزل y من المعادلة الأولى
8x - y = 16
8x - y - 8x = 16 - 8x
y = -16 + 8x
y = 8x - 16
أعوض ( 8x - 16 ) في المعادلة الثانية
العبارة الرياضية الأخيرة خاطئة ، إذن لا يوجد حل لنظام المعادلتين .
.....................................................................................................................................................................................................................................................................
8)
أعزل y من المعادلة الثانية :
أعوض قيمة y في المعادلة الاولى :
6x - 9y = 18
إذن لنظام المعادلتين عدد لا نهائي من الحلول.
........................................................................................................................................................................................................................................................................
9) y + 3x + 6 = 0
y + 6x + 24 = 0
أعزل قيمة y من المعادلة الأولى :
y + 3x + 6 = 0
y + 3x + 6 - 3x -6 = 0 - 3x -6
y = - 3x -6
أعوض قيمة y من المعادلة الاولى في المعادلة الثانية :
y + 6x + 24 = 0
x = - 6
أعوض 6 - في المعادلة الأولى :
y + 3x + 6 = 0
y + 3 ( - 6 ) + 6 = 0
y - 18 + 6 = 0
y - 12 = 0
y - 12 + 12 = 0 + 12
y = 12
إذن حل النظام هو ( 12 , 6 - )
............................................................................................................................................................................................................................................................................
10) مزرعة : مزرعة حيوانات فيها دجاج وأرانب ، إذا عددت رؤوسها سأجدها 18 رأساً ، وإذا عددت أرجلها سأجدها 50 رجلاً ،
كم دجاجة وكم أرنباً في هذه المزرعة؟
الحل :
المعطيات : - عدد الدجاج والأرانب 18
- عدد أرجل الدجاج والأرانب 50 رجلاً
علماً أن : للدجاجة اثنتان من الأرجل
وللأرانب 4 من الأرجل
المطلوب : عدد الدجاج وعدد الأرانب
المتغيرات : x : عدد الدجاج
y: عدد الأرانب
المعادلات:
x + y = 18
2x + 4y = 50
أحل نظام المعادلات الخطية :
أعزل y من المعادلة الأولى :
x + y = 18
x + y - x = 18 - x
y = 18 - x
أعوض بدلاً من y في المعادلة الثانية :
2x + 4y = 50
2x + 4 ( 18 - x ) = 50
2x + 72 - 4x = 50
x = 11
أعوض 11 بدلاً من x في المعادلة الأولى :
x + y = 18
11 + y = 18
11 + y - 11 = 18 - 11
y = 7
( 7 , 11 ) حل لنظام المعادلتين ،
إذن عدد الدجاج هو 11
عدد الأرانب هو 7
..............................................................................................................................................................................................................................................................................................................
فاكهة : اشترى مراد وفؤاد برتقالاً وتفاحاً من النوع نفسه ، فدفع مراد 3.25 JD عند شرائه 5kg برتقالاً و 1kg تفاحاً ،
ودفع فؤاد 3.75 JD عند شرائه 3Kg تفاحا و 3kg برتقالاً .
11) اكتب نظاماً من معادلتين خطيتين يمثل المسألة، ثم أحله لأجد سعر الكيلو غرام الواحد من كل من التفاح والبرتقال.
12) إذا اشترت منال 2kg من نوع التفاح نفسه و 2kg من نوع البرتقال نفسه ، فما المبلغ الذي دفعته.
الحل:
11) المعطيات : - مشتريات مراد : دفع 3.25 JD مقابل 5kg برتقال و 1kg تفاح
- مشتريات فؤاد : دفع 3.75 JD مقابل 3kg تفاح و 3kg برتقال
المطلوب : - كتابة نظام معادلتين خطيتين يمثل المسألة
- سعر الكيلو غرام الواحد لكل من البرتقال والتفاح
المتغيرات: x: سعر كليو التفاح
y: سعر كيلو البرتقال
المعادلات:
x + 5y = 3.25
3x + 3y = 3.75
أحل نظام المعادلتين :
أعزل x من المعادلة الأولى :
x + 5y = 3.25
x + 5y - 5y = 3.25 - 5y
x = 3.25 - 5y
أعوض بدلاً من x في المعادلة الثانية :
3x + 3y = 3.75
3 ( 3.25 - 5y ) + 3y = 3.75
9.75 - 15y + 3y = 3.75
9.75 - 12y = 3.75
9.75 - 12y - 9.75 = 3.75 - 9.75
y = 0.5
أعوض 0.5 بدلاً من y في المعادلة الأولى :
x + 5y = 3.25
x + 5 ( 0.5 ) = 3.25
x + 2.5 = 3.25
x + 2.5 - 2.5 = 3.25 - 2.5
x = 0.75
إذن ثمن كيلو التفاح 0.75 JD
وثمن كيلو البرتقال 0.5 JD
........................................................................................................................................................................
12) مشتريات منال :
2x + 2y = ?
2 ( 0.75 ) + 2 ( 0.5 ) = ?
1.5 + 1 = 2.5
إذن المبلغ الذي دفعته منال هو : 2.5 JD
.............................................................................................................................................................................................................................................................................
13) سياحة : يبين الجدول الآتي أعداد السياح في موقعين أثريين في أحد الأعوام ، ومعدل الزيادة المئوية في أعداد السياح ( بالآلاف )بعد ذلك العام :
|
أعداد السياح (بالالاف ) |
معدل الزيادة في أعداد السياح ( بالالاف لكل عام) |
|
| الموقع أ | 57 | 1.1 |
| الموقع ب | 61 | 0.7 |
إذا استمرت الزيادة في أعداد السياح وفق المعدلات ، فبعد كم عام يمكن أن تتساوى أعداد السياح في الموقعين ؟ وكم يبلغ عددهم حينئذ؟
الحل:
المعطيات : - الموقع أ : أعداد السياح في عام معين 57000 سائح
معدل الزيادة السنوية 1100 سائح
- الموقع ب : أعداد السياح في العام نفسه 61000 سائح
معدل الزيادة 700 سائح
المطلوب : بعد كم عام يمكن أن تتساوى أعداد السياح في الموقعين
المتغيرات : x: عدد السياح
y: عدد الأعوام
المعادلات :
x = 1100y + 5700
x = 700y + 61000
أعوض ( 1100y + 57000) بدلاً من x في المعادلة الثانية :
x = 700 y + 61000
1100 y + 57000 = 700 y + 61000
1100y + 57000 - 700 y = 700 y + 61000 - 700 y
400 y + 57000 = 61000
400 y + 57000 - 57000 = 61000 - 57000
400 y = 4000
y = 10
أعوض 10 بدلاً من x في المعادلة الأولى:
x = 1100 y + 5700
x = 1100 ( 10 ) + 5700
x = 11000 + 5700
x = 68000
إذن يتساوى عدد السياح في الموقعين بعد 10 أعوام .
ويكون عدد السياح في كل موقع 68000 سائح.
........................................................................................................................................................................................................................................................................
14) هندسة : إذا كانت القيمة العددية لمحيط المثلث المجاور تساوي القيمة العددية لمساحته ، فما قيمة x ؟
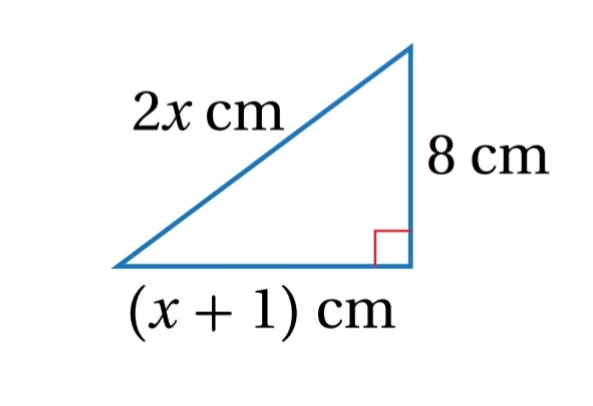
الحل :
مجموع أطوال أضلاعه = محيط المثلث
محيط المثلث =
محيط المثلث =
مساحة المثلث =
مساحة المثلث =
حسب معطيات المسألة :
القيمة العددية لمحيط المثلث = القيمة العددية لمساحة المثلث
4x + 4 = 3x + 9
4x + 4 - 3x = 3x + 9 - 3x
x + 4 = 9
x + 4 - 4 = 9 - 4
x = 5
قيمة x هي 5
......................................................................................................................................................................................................................................................................
15) تبرير : أجد قيمتي الثابتين a و b في نظام المعادلات الخطية الآتي ، حيث الزوج المرتب ( 1 , 9- ) هو حل النظام ، مبرراً إجابتي :
ax + by = - 31
ax - by = - 41
الحل:
الزوج المرتب ( 1 , 9- ) هو حل للنظام
إذن يحقق المعادلتين وبالتالي أعوض x = 9 , y = 1 في المعادلتين فيكون :
ax + by = - 31
a ( -9 ) + b ( 1 ) = - 31
المعادلة الأولى
ax - by = - 41
a ( - 9 ) - b ( 1 ) = - 41
المعادلة الثانية
لحساب a , b أحل نظام المعادلتين الخطيتين :
المعادلة الأولى
- المعادلة الثانية
أعزل b من المعادلة الأولى :
b = 9a - 31
أعوض 9a - 31 بدلاً من b في المعادلة الثانية :
a = 4
أعوض a = 4 في المعادلة الأولى :
إذن قيمة : a = 4 , b = 5
......................................................................................................................................................................................................................................................................
16) مسألة مفتوحة : اكتب نظام معادلات خطية مكوناً من معادلتين خطيتين حيث يمثل الزوج المرتب ( 5- , 3 ) حلاً لإحدى المعادلتين فقط،
ويمثل الزوج المرتب ( 7 , 1- ) حلاً للنظام.
الحل:
أفرض أن المعادلة الأساسية هي
y = ax + b
أعلم أن ( 5- , 3 ) ، ( 7 , 1- ) كلا الزوجين هو حل للمعادلة السابقة ، فيكون لدينا :
أعوض ( 5- , 3 ) في المعادلة الأساسية
أعوض ( 7 , 1- ) في المعادلة الأساسية
أحل نظام المعادلتين السابقتين لحساب a , b
من المعادلة الأولى أعزل b فيكون
b = - 5 - 3a
أعوض بدلاً من b في المعادلة الثانية :
a = - 3
أعوض b في احدى المعادلتين السابقتين مثلاً المعادلة الثانية :
7 = 3 + b
7 - 3 = 3 + b - 3
4 = b
b = 4
إذن المعادلة الأولى التي تحقق الزوجين هي :
y = - 3x + 4
وبما أن المعادلة الثانية تحقق الزوج ( 7 , 1 - ) ، أختار مثلاً المعادلة :
y = - x + 6
إذن جملة المعادلتين هي :
y = - 3x + 4
y = -x + 6
............................................................................................................................................................................................................................................................................
17) تتألف دفعة من خريجي دورة للدفاع المدني من 240 شخصاً ، نسبة الذكور فيها الى الاناث 7 : 5 ،
أكتب نظاماً من معادلتين خطيتين يمثل المسألة ، ثم احله لأجد عدد الذكور وعدد الاناث في هذه الدفعة من الخريجين.
الحل :
المعطيات : - عدد أفراد الدورة 240 شخص
- نسبة الذكور الى الاناث 7 : 5 أي
المطلوب : أكتب نظام من معادلتين يمثل المسألة ، وأحل النظام لأجد عدد الذكور وعدد الاناث
المتغيرات : x : عدد الذكور
y : عدد الاناث
المعادلات :
x + y = 240
7x - 5y = 0
أعزل x من المعادلة الأولى
x + y = 240
x = 240 - y
وأعوض في المعادلة الثانية :
7x - 5y = 0
7 ( 240 - y ) - 5y = 0
1680 - 7y - 5y = 0
1680 - 12y = 0
1680 - 12y - 1680 = - 1680
y = 140
أعوض y = 140 في المعادلة الأولى :
x + 140 = 240
x + 140 - 140 = 240 - 140
x = 100
إذن : عدد الذكور 140 فرد
عدد الاناث 100 فرد
........................................................................................................................................................................................................................................................................
18) كيف أحل نظام معادلات خطية مكوناً من معادلتين بالتعويض ؟
الحل:
لحل نظام المعادلات الخطية المكونة من معادلتين بالتعويض
1- أعزل أحد المتغيرات في أحد الطرفين
2- أعوض قيمة المتغير الذي حصلت عليه من المعادلة السابقة في المعادلة الأخرى.
3- بعد ذلك أبسط وأحصل على قيمة المتغير وأعوض في احدى المعادلتين لأحصل على قيمة المتغير الثاني.
4- بذلك تحصل على زوج مرتب يمثل حلاً لنظام المعادلتين الخطيتين.
............................................................................................................................................................................................................................................................................
حل مسائل كتاب التمارين :
اكتب بجانب كل نظام معادلات مما يأتي رمز التمثيل البياني المناسب له ، مبرراً إجابتي :
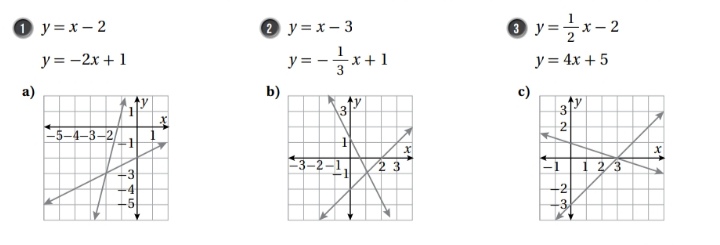
الحل :
أحل كل من انظمة المعادلات السابقة لايجاد نقطة التقاطع في كل نظام :
1) y = x - 2
y = -2x + 1
أعوض y من المعادلة الأولى في المعادلة الثانية :
y = - 2x + 1
x - 2 = - 2x + 1
x - 2 + 2x + 2 = -2x + 1 + 2x + 2
3x = 3
x = 1
أعوض x = 1 في المعادلة الاولى :
y = x - 2
y = 1 - 2
y = - 1
إذن حل النظام ( 1- , 1 ) وهي ذاتها نقطة التقاطع في الشكل b
إذن رمز التمثيل البياني للنظام رقم 1 هو b
....................................................................................................................................
2) y = x - 3
أعوض قيمة y من المعادلة الاولى في المعادلة الثانية
x = 3
أعوض x = 3 في المعادلة الأولى :
y = x - 3
y = 3 - 3
y = 0
إذن حل النظام ( 0 , 3 ) وهي ذاتها نقطة التقاطع في الشكل c
إذن رمز التمثيل البياني للنظام رقم 2 هو c
...................................................................................................................
3)
أعوض قيمة y من المعادلة الثانية في المعادلة الاولى
7x = - 14
x = - 2
أعوض x = - 2 في المعادلة الثانية :
y = 4x + 5
y = 4 ( - 2 ) + 5
y = - 8 + 5
y = - 3
إذن حل النظام ( 3- , 2 - ) وهي ذاتها تمثل نقطة التقاطع في الشكل a
إذن رمز التمثيل البياني للنظام رقم 3 هو a
...............................................................................................................................................................................................................................................................................
أحل كلاً من أنظمة المعادلات الآتية مستعملاً التعويض:
4) y = x + 1
x + y = 7
أعوض قيمة y من المعادلة الأولى في المعادلة الثانية :
x + y = 7
x + ( x + 1 ) = 7
x + x + 1 = 7
2x + 1 = 7
2x + 1 - 1 = 7 - 1
2x = 6
x = 3
أعوض x = 3 في المعادلة الأولى:
y = x + 1
y = 3 + 1
y = 4
إذن حل النظام ( 4 , 3 )
...........................................................................................................................................................................................................................................................................
5) y = x + 5
2x + 3y = 15
أعوض y من المعادلة الأولى في المعادلة الثانية :
2x + 3y = 15
2x + 3 ( x + 5 ) = 15
2x + 3x + 15 = 15
5x + 15 - 15 = 15 - 15
5x = 0
x = 0
أعوض x = 0 في المعادلة الأولى
y = x + 5
y = 0 + 5
y = 5
إذن حل النظام ( 5 , 0 )
...............................................................................................................................................................................................................................................................................
6) x = 3 - y
x - y = - 1
أعوض قيمة x من المعادلة الاولى في المعادلة الثانية :
x - y = -1
( 3 - y ) - y = - 1
3 - y -y = -1
3 - 2y = - 1
3 - 2y - 3 = -1 - 3
y = 2
أعوض y = 2 في المعادلة الأولى
x = 3 - y
x = 3 - 2
x = 1
إذن حل النظام ( 2 , 1 )
...............................................................................................................................................................................................................................................................................
7)
y = 17 - 2x
أعوض قيمة y من المعادلة الثانية في المعادلة الأولى :
أعوض x = 8 في المعادلة الثانية :
y = 17 - 2x
y = 17 - 2 ( 8 )
y = 17 - 16
y = 1
إذن حل النظام ( 1 , 8 )
.............................................................................................................................................................................................................................................................................
8) 3x - 4y = 2
y - 3x = -5
أعزل y من المعادلة الثانية :
y - 3x = - 5
y - 3x + 3x = -5 + 3x
y = 3x - 5
أعوض ( 3x - 5 ) في المعادلة الاولى :
3x - 4y = 2
3x - 4 ( 3x - 5 ) = 2
3x - 12x + 20 = 2
x = 2
أعوض x = 2 في المعادلة الثانية:
y - 3x = - 5
y - 3 ( 2 ) = - 5
y - 6 = - 5
y - 6 + 6 = - 5 + 6
y = 1
إذن حل النظام ( 1 , 2 )
.............................................................................................................................................................................................................................................................................
9) y - x = 3
y - 2x = 1
أعزل y من المعادلة الأولى :
y - x = 3
y - x + x = 3 + x
y = x + 3
أعوض ( x + 3 ) في المعادلة الثانية :
y - 2x = 1
x + 3 - 2x = 1
- x = - 2
x = 2
أعوض 2 في المعادلة الأولى :
y - x = 3
y - 2 = 3
y - 2 + 2 = 3 + 2
y = 5
إذن حل النظام ( 5 , 2 )
............................................................................................................................................................................................................................................................................
10) 2x - y = 14
أعزل y من المعادلة الأولى :
2x - y = 14
2x - y - 2x = 14 - 2x
y = 2x - 14
أعوض قيمة y في المعادلة الثانية :
x = 8
أعوض 8 في المعادلة الأولى :
2 ( 8 ) - y = 14
16 - y = 14
16 - y - 16 = 14 - 16
y = 2
إذن حل النظام ( 2 , 8 )
.................................................................................................................................................................................................................................................................................
11) 5x - 3y = 18
أعزل y من المعادلة الثانية :
2y = 2x - 8
y = x - 4
أعوض y = x - 4 في المعادلة الأولى :
5x - 3y = 18
5x - 3 ( x - 4 ) = 18
5x - 3x + 12 = 18
2x + 12 - 12 = 18 - 12
2x = 6
x = 3
أعوض x = 3 في المعادلة الثانية :
2y = -2
y = - 1
إذن حل النظام ( 1 - , 3 )
...............................................................................................................................................................................................................................................................................
12) y + 3x = - 5
y + 6x = - 11
أعزل y من المعادلة الأولى :
y + 3x = - 5
y + 3x - 3x = - 5 - 3x
y = -5 - 3x
أعوض قيمة y في المعادلة الثانية :
3x = - 6
x = -2
( طريقة تعويض ثانية ) : بما أن y = -5 -3x أعوض x = -2 بهذه المعادلة :
y = -5 - 3x
y = - 5 - 3 ( - 2 )
y = -5 + 6
y = 1
إذن حل النظام ( 1 , 2- )
...............................................................................................................................................................................................................................................................................
13 ) تملك فاتن وفدوى 75 JD ، فإذا كان الملغ الذي تملكه فدوى مثلي المبلغ الذي تملكه فاتن ،
فاكتب نظاما من معادلتين خطيتين يمثل المسألة ، ثم أحله لأجد المبلغ الذي تملكه كل منهما.
الحل :
المعطيات : - تملك فاتن وفدوى 75 JD
- المبلغ الذي تملكه فدوى مثلي المبلغ الذي تملكه فاتن
المطلوب : - كتابة معادلتين خطيتين تمثل المسألة
- إيجاد المبلغ الذي تملكه كل من فاتن وفدوى
المتغيرات : x : المبلغ الذي تملكه فاتن
y : المبلغ الذي تملكه فدوى
المعطيات :
x + y = 75
y = 2x
أعوض 2x بدلاً من y في المعادلة الأولى
x + y = 75
x + 2x = 75
3x = 75
x = 25
أعوض 25 بدلاً من x في المعادلة الثانية
y = 2x
y = 2 ( 25 )
y = 50
إذن مبلغ فاتن 25 JD
مبلغ فدوى 50 JD
................................................................................................................................................................................................................................................................................
14 ) أعمار : عمر طارق يساوي ثلاثة أمثال عمر أخته صفاء ، إذا كان مجموع عمريهما يساوي 36 سنة فكم عمر كل منهما ؟
الحل :
المعطيات : - عمر طارق ثلاثة أمثال عمر أخته صفاء
- مجموع عمريهما 36 سنة
المطلوب : إيجاد المبلغ الذي يملكه كل من طارق واخته
المتغيرات : x : عمر طارق
y : عمر أخته صفاء
المعادلات :
x = 3y
x + y = 36
أعوض 3y بدلاً من x في المعادلة الثانية :
x + y = 36
3y + y = 36
4y = 36
y = 9
أعوض 9 بدلاً من y في المعادلة الأولى :
x = 3 ( 9 )
x = 27
إذن : عمر طارق 27 سنة
عمر أخته صفاء 9 سنوات
................................................................................................................................................................................................................................................................................
15) كتب : مجموع عدد صفحات كتابين سيقرأهما جلال 150 صفحة ، إذا كان عدد صفحات الكتاب الأول يقل عن نصف عدد صفحات الكتاب الثاني بمقدار 15 صفحة ،
فكم صفحة في كل كتاب ؟
الحل :
المعطيات : - مجموع عدد صفحات كتابين 150 صفحة
- عدد صفحات الكتاب الاول يقل عن نصف عدد صفحات الكتاب الثاني بمقدار 15
المطلوب : عدد صفحات كل كتاب
المتغيرات : x : عدد صفحات الكتاب الأول
y : عدد صفحات الكتاب الثاني
المعادلات :
x + y = 150
اعوض قيمة x من المعادلة الثانية في المعادلة الأولى :
أعوض 110 بدلاً من y في المعادلة الثانية :
x = 40
إذن عدد صفحات الكتاب الأول 40 صفحة
عدد صفحات الكتاب الثاني 110 صفحة
...............................................................................................................................................................................................................................................................................
16) أعداد : كتبت علياء عددين مجموعهما 37 ، والفرق بينهما يساوي 14 ، فما العددان ؟
الحل :
المعطيات : مجموع العددين 37
فرق العددين 12
المطلوب : ما هما العددان؟
المتغير : x : العدد الأول
y : العدد الثاني
المعادلات:
x + y = 37
x - y = 14
نعزل x في المعادلة الأولى :
x + y = 37
x + y - y = 37 - y
x = 37 - y
نعوض قيمة x في المعادلة الثانية :
x - y = 14
37 - y - y = 14
37 - 2y - 37 = 14 - 37
y = 11.5
نعوض y = 11.5 في المعادلة الأولى :
x + y = 37
x + 11.5 = 37
x = 37 - 11.5
x = 25.5
إذن العدد الأولى = 25.5
والعدد الثاني = 11.5
...............................................................................................................................................................................................................................................................................