حل نظام من معادلتين خطيتين بيانياً
يتكون نظام المعادلات الخطية من معادلتين خطيتين أو أكثر لها المتغيرات نفسها.
مثال: نظام مكون من معادلتين خطيتين
y = 2x - 5
y = 3x + 4
.............................................................................................................................................................................................................................................
تعريف حل نظام المعادلات الخطية بمتغيرين: هو زوج مرتب يحقق كل معادلة في النظام .
.............................................................................................................................................................................................................................................
مثال ( 1 ) : أحدد إذا كان الزوج المرتب يمثل حلاً لنظام المعادلات الخطية المعطى في كل مما يأتي :
1) 3x + y = 11
2x - 2y = 2
أعوض الزوج المرتب ( 2 , 3 ) في كلا المعادلتين:
حيث : y = 2 , x = 3
| المعادلة ( 2 ) | المعادلة ( 1 ) |
|
2x - 2y = 2 2 ( 3 ) - 2 ( 2 ) = 2 6 - 4 = 2 2 = 2 صحيح |
3x + y = 11 3 ( 3 ) + 2 = 11 9 + 2 = 11 11 = 11 صحيح |
2) , x - y = 5
أعوض الزوج المرتب في كلا المعادلتين حيث y = 2 , x = 7
| المعادلة ( 2 ) | المعادلة ( 1 ) |
|
خطأ |
x - y = 5 7 - 2 = 5 5 = 5 صحيح |
ألاحظ أن الزوج المرتب ( 2 , 7 ) يمثل حلاً للمعادلة الأولى ، ولكنه لا يمثل حلاً للمعادلة الثانية ،
إذن ( 2 , 7 ) لا يمثل حلاً لنظام المعادلتين.
.............................................................................................................................................................................................................................................
مثال ( 2 ) : أحل نظام المعادلات الآتي بيانياً
y = x - 3
y = - x - 1
أحدد نقطتين من المعادلة الاولى y = x - 3
أفرض مثلاً x = 0 فتكون :
y = 0 - 3
y = -3
النقطة ( 3- ، 0 )
ثم أفرض مثلاً x = 1 فتكون
y = 1 - 3
y = - 2
النقطة ( 2- , 1 )
أحدد نقطتين من المعادلة الثانية : y = -x - 1
أفرض مثلاً x = 0 فتكون :
y = 0 - 1
y = -1
النقطة (1- , 0 )
ثم أفرض مثلاً x = 1 فتكون:
y = -1 -1
y = -2
النقطة ( 2- , 1)
تمثيل المعادلتين على المستوى الاحداثي:
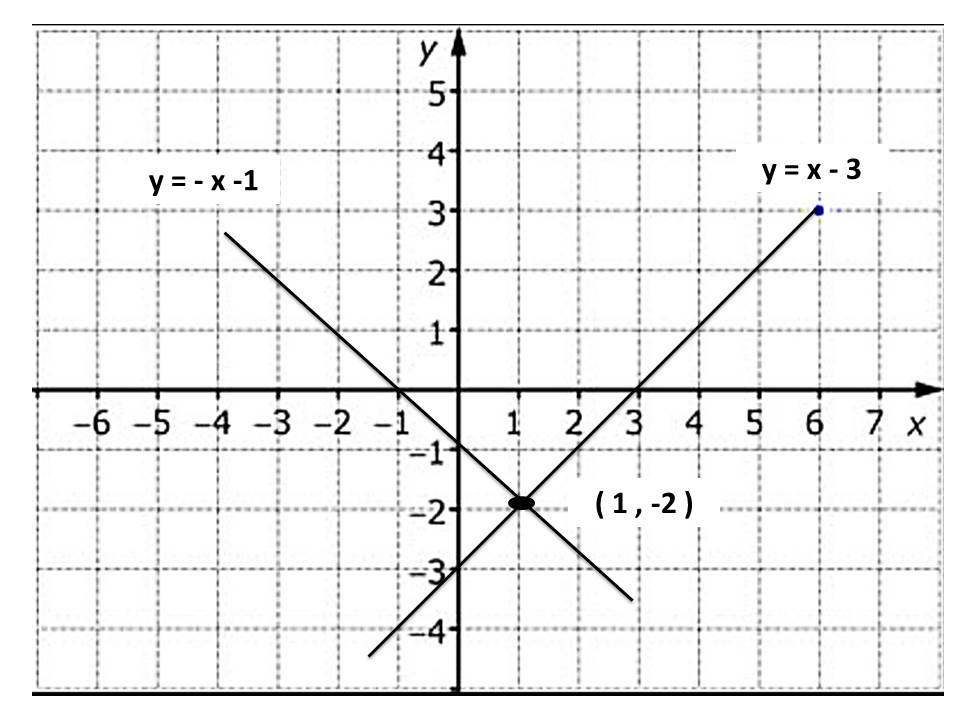
ألاحظ أن المستقيمين تقاطعا في النقطة ( 2- , 1 )
إذن الحل هو : x = 1
y = -2
أتحقق من صحة الحل :
أعوض الزوج المرتب ( 2- , 1 ) في المعادلتين :
| المعادلة ( 2 ) | المعادلة ( 1 ) |
|
y = - x - 1
صحيح |
صحيح |
إذن حل النظام ( 2- , 1 )
..........................................................................................................................................................................................................................................................
مثال ( 3 ) : أحل كلاً من أنظمة المعادلات الآتية بيانياً :
1 ) y = 2x + 4
y = 2x - 1
أحدد نقطتين من المعادلة الأولى y = 2x + 4
أفرض مثلاً x = 0 فتكون :
y = 2x + 4
y = 2 ( 0 ) + 4
y = 4
النقطة ( 4 , 0 )
أفرض مثلاً x = 1 فتكون:
y = 2x + 4
y = 2 ( 1 ) + 4
y = 2 + 4
y = 6
النقظة ( 6 , 1 )
أحدد نقطتين من المعادلة الثانية y = 2x - 1
أفرض مثلاً x = 0 فتكون :
y = 2x -1
y = 2 ( 0 ) -1
y = 0 - 1
y = -1
النقطة ( 1- , 0 )
أفرض مثلاً x = 1 فتكون :
y = 2x - 1
y = 2 ( 1 ) -1
y = 2 - 1
y = 1
النقطة ( 1+ , 1+ )
تمثيل المعادلتين على المستوى الاحداثي:
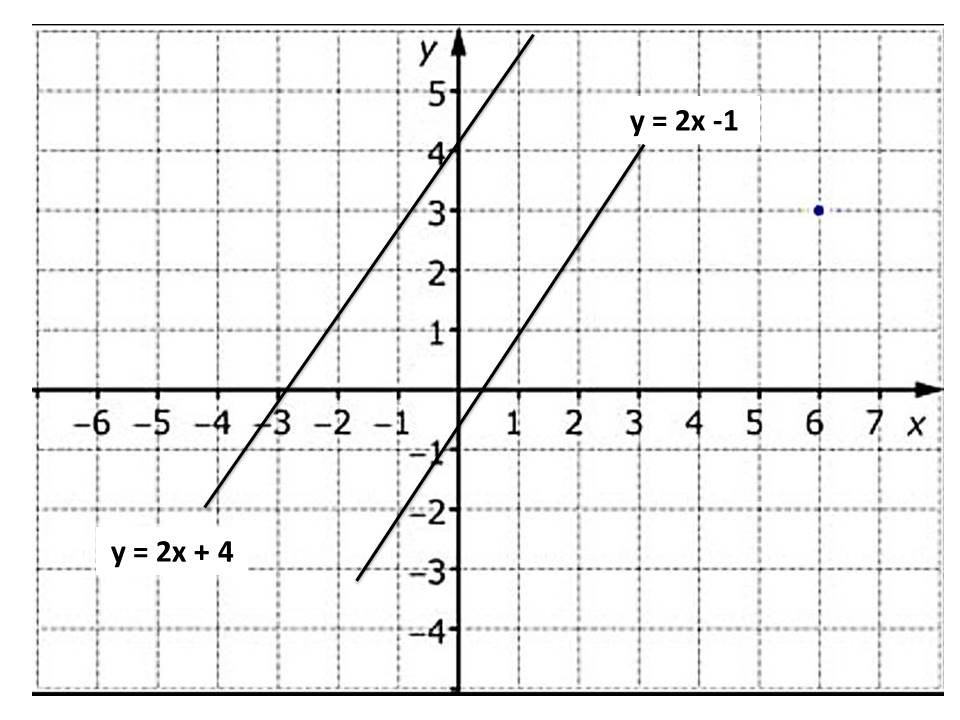
ألاحظ أن المستقيمين متوازيان إذن لا يوجد حل لهذا النظام .
............................................................................................................................................................................................................................................
2 ) 9x - 6y = 24
6x - 4y = 16
أحدد نقطتين من المعادلة الأولى 9x - 6y = 24
أفرض مثلاً x = 0 فيكون :
9 ( 0 ) - 6 y = 24
y = -4
النقطة ( 4- , 0 )
أفرض مثلاً x = 2 فيكون :
9(2) - 6y = 24
18 - 6y = 24
18 - 6y - 18 = 24 - 18
- 6y = 6
y = -1
النقطة ( 1- , 2 )
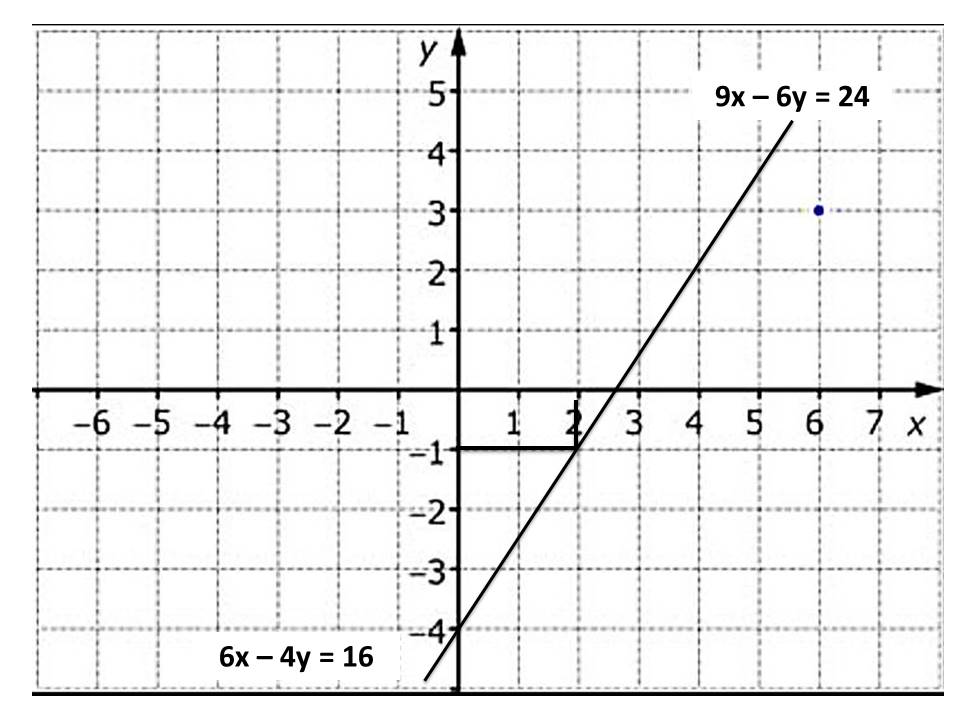
الاحظ أن كلا المعادلتين لهما التمثيل البياني ذاته ، إذن يوجد عدد لا نهائي من الحلول .
............................................................................................................................................................................................................................................................
مسألة حياتية :
منطاد : منطادان ارتفاع أحدهما 4m عن سطح الارض ، ويزداد ارتفاعه بمعدل ثابت مقداره 5m لكل دقيقة ، والمنطاد الاخر ارتفاعه 10m عن سطح الارض ،
ويزداد ارتفاعه بمعدل ثابت مقداره 3m لكل دقيقة ، بعد كم دقيقة يصبح للمنطادين الارتفاع نفسه ؟
الحل:
المعطيات : المنطاد الأول : 1- ارتفاعه 4m عن سطح الارض
2- يزداد ارتفاعه بمعدل 5m لكل دقيقة
المنطاد الثاني : 1- ارتفاعه 10m عن سطح الارض
2- يزداد ارتفاعه بمعدل 3m لكل دقيقة
المطلوب: كم دقيقة يصبح للمنطادين الارتفاع نفسه
المتغير : أفرض x عدد الدقائق
أفرض y ارتفاع المنطاد
المعادلات: y = 5x + 4
y = 3x + 10
لايجاد متى يصبح للمنطادين الارتفاع نفسه أمثل المعادلتين بيانياً لحلهما :
المعادلة الأولى : y = 5x + 4
أفرض x = 0 فتكون:
y = 5 ( 0 ) + 4
y = 0 + 4
y = 4
النقطة ( 4 , 0 )
أفرض مثلاً x = 1 فتكون:
y = 5 ( 1 ) + 4
y = 5 + 4
y = 9
النقطة ( 9 , 1 )
المعادلة الثانية : y = 3x + 10
أفرض x = 0 فتكون:
y = 3 ( 0 ) + 10
y = 0 + 10
y = 10
النقطة ( 10 , 0 )
أفرض مثلاً x = 1 فتكون:
y = 3 ( 1 ) + 10
y = 3 + 10
y = 13
النقطة ( 13 , 1 )
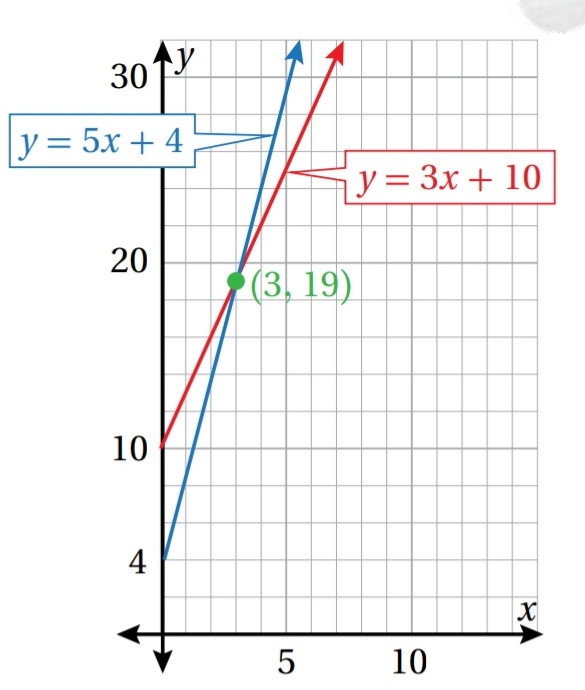
ألاحظ أن النقطتين تتقاطعان عند النقطة ( 19 , 3 )
x = 3
y = 19
إذن يصبح للمنطادين الارتفاع نفسه بعد 3 دقائق ويكون ارتفاعهما على سطح الارض 19m
.............................................................................................................................................................................................................................................