رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 130

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْفِرْجارَ لِرَسْمِ مُثَلَّثٍ أَطْوالُ أَضْلاعِهِ : 2cm, 4cm , 5cm

الحل : 

 

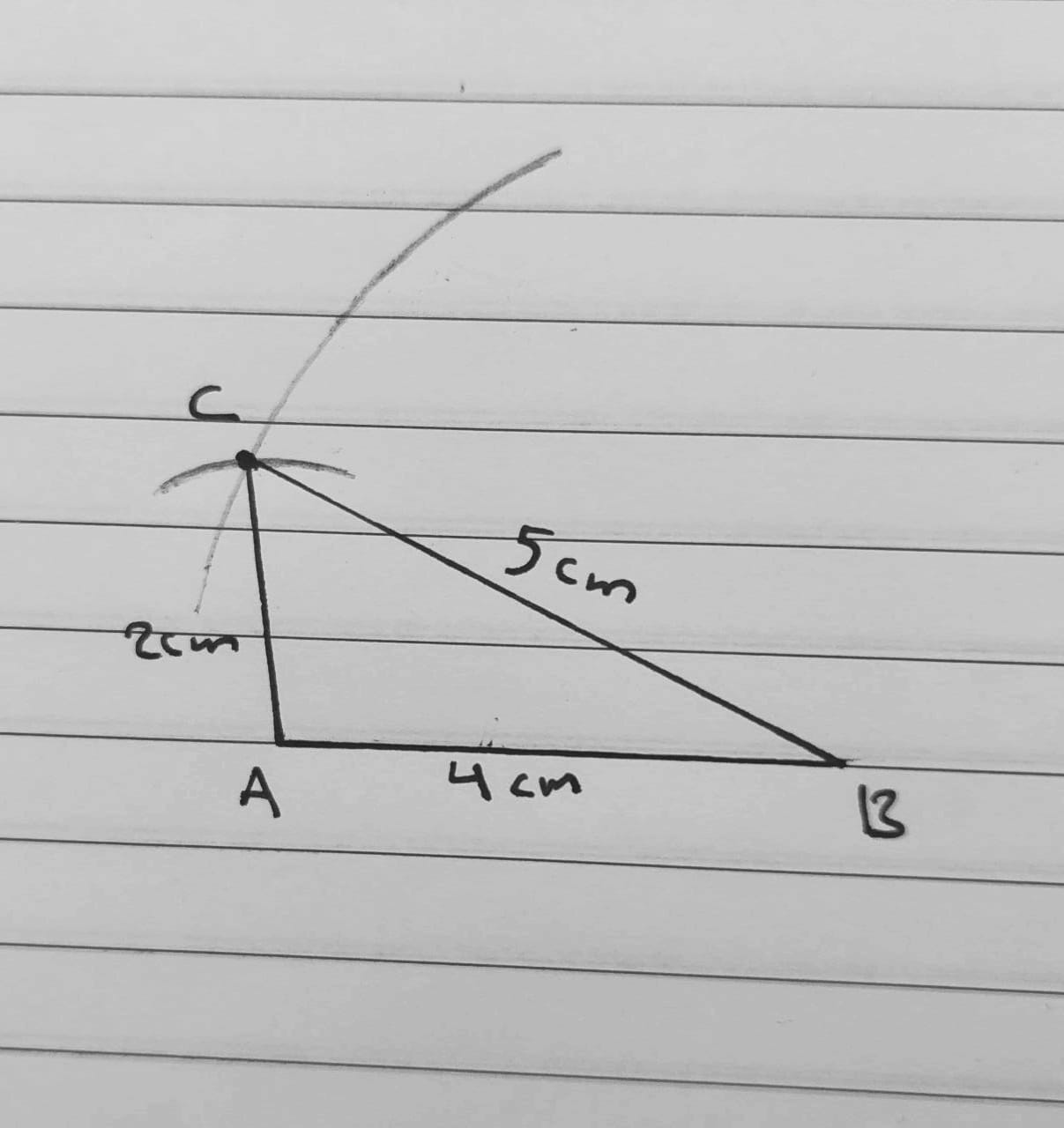
أتحقق من فهمي صفحة 131

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ لِرَسْمِ الْمُثَلَّثِ XYZ ، إذا كان : $YZ = 6 cm , \angle Y = 30° , \angle Z = 115° ,$

الحل : 

 

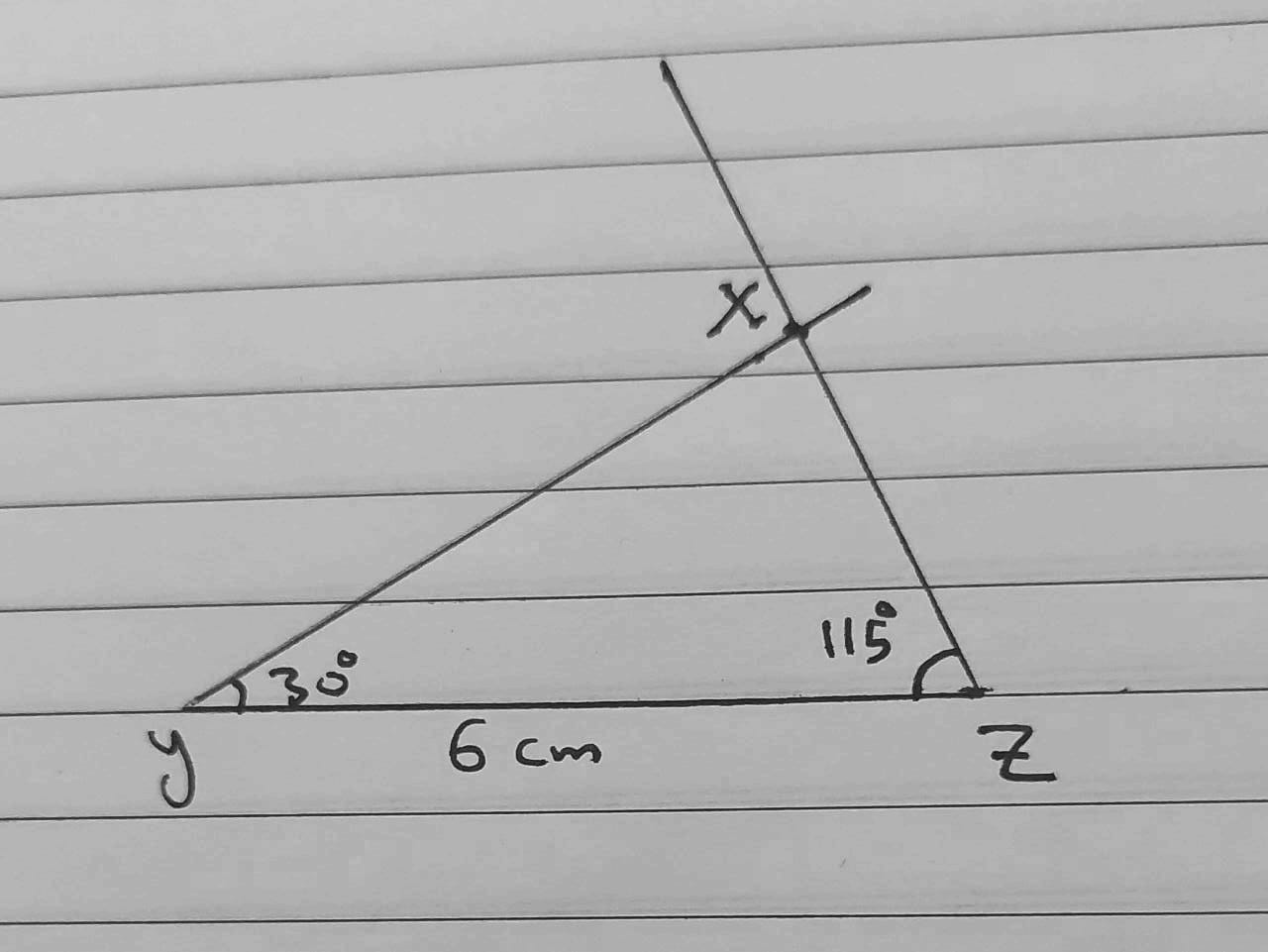
أتحقق من فهمي صفحة 132

أسَْتعَْمِلُ المِْسْطرََةَ وَالمِْنقَْلةََ لرَِسْمِ المُْثلَثَِّ ABC الْمُتَطابِقِ الضِّلْعَيْنِ طولُ كُلِّ ضِلْعٍ مِنْهُما $6 cm$ ، وَقِياسُ الزّاوِيَةِ الْمَحْصورَةِ

بينهما $100°$

الحل : 

 

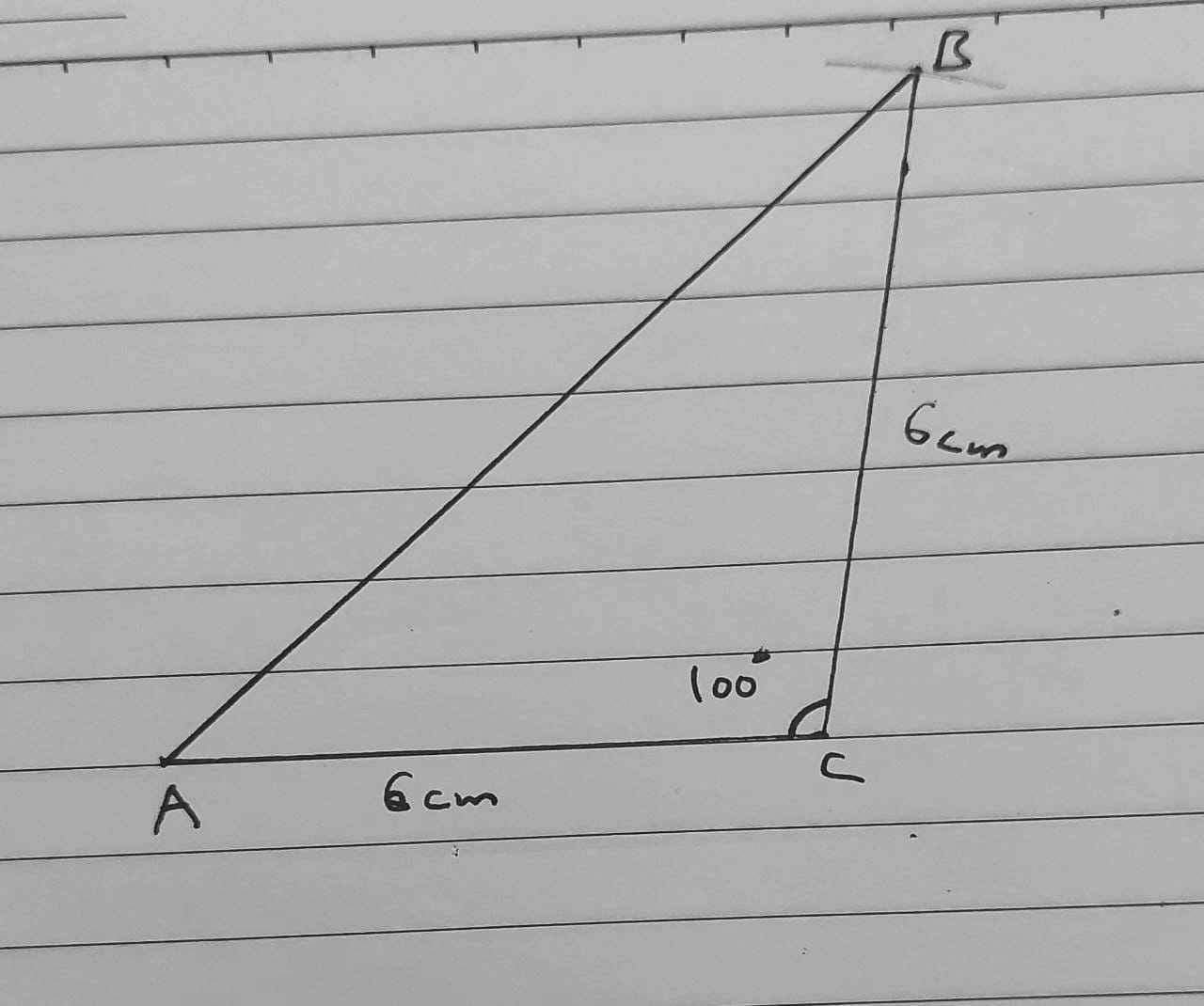
أتحقق من فهمي صفحة 133

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ وَالْفِرْجارَ لِرَسْمِ الْمُثَلَّثِ IHJ إِذا كانَ: $JH = 8 cm , IJ= 5 cm , m\angle H = 43°$

الحل : 

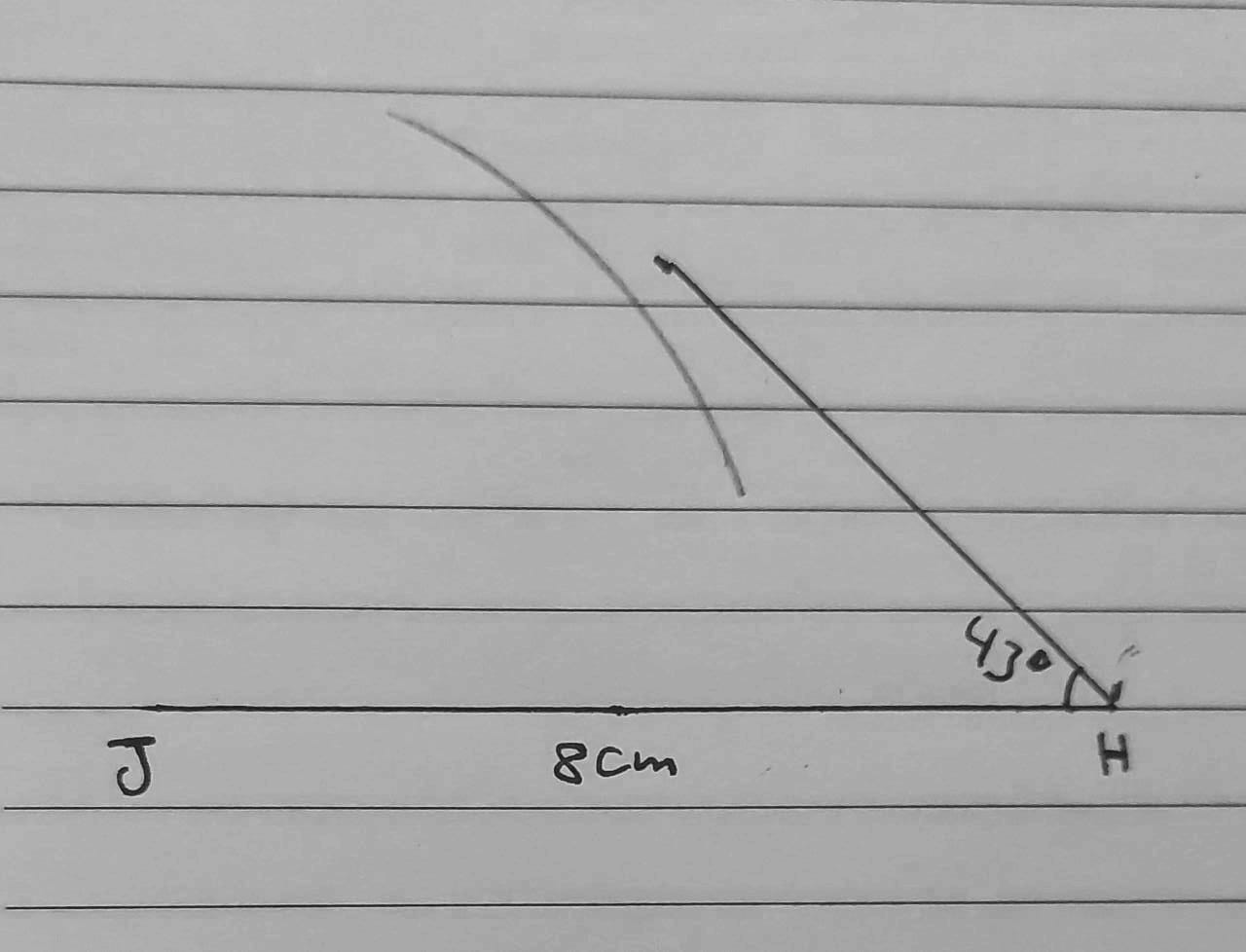
نلاحظ أن القوس لا يقطع ضلع الزاوية ، فهنا لا يُمكن رسم هذا المثلث.

---

أسئلة أتدرب وأحل المسائل

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْفِرْجارَ لِرَسْمِ  Δ ABC ، حَيْثُ: 

1)  AB = 3 cm , BC = 5 cm , AC = 7 cm

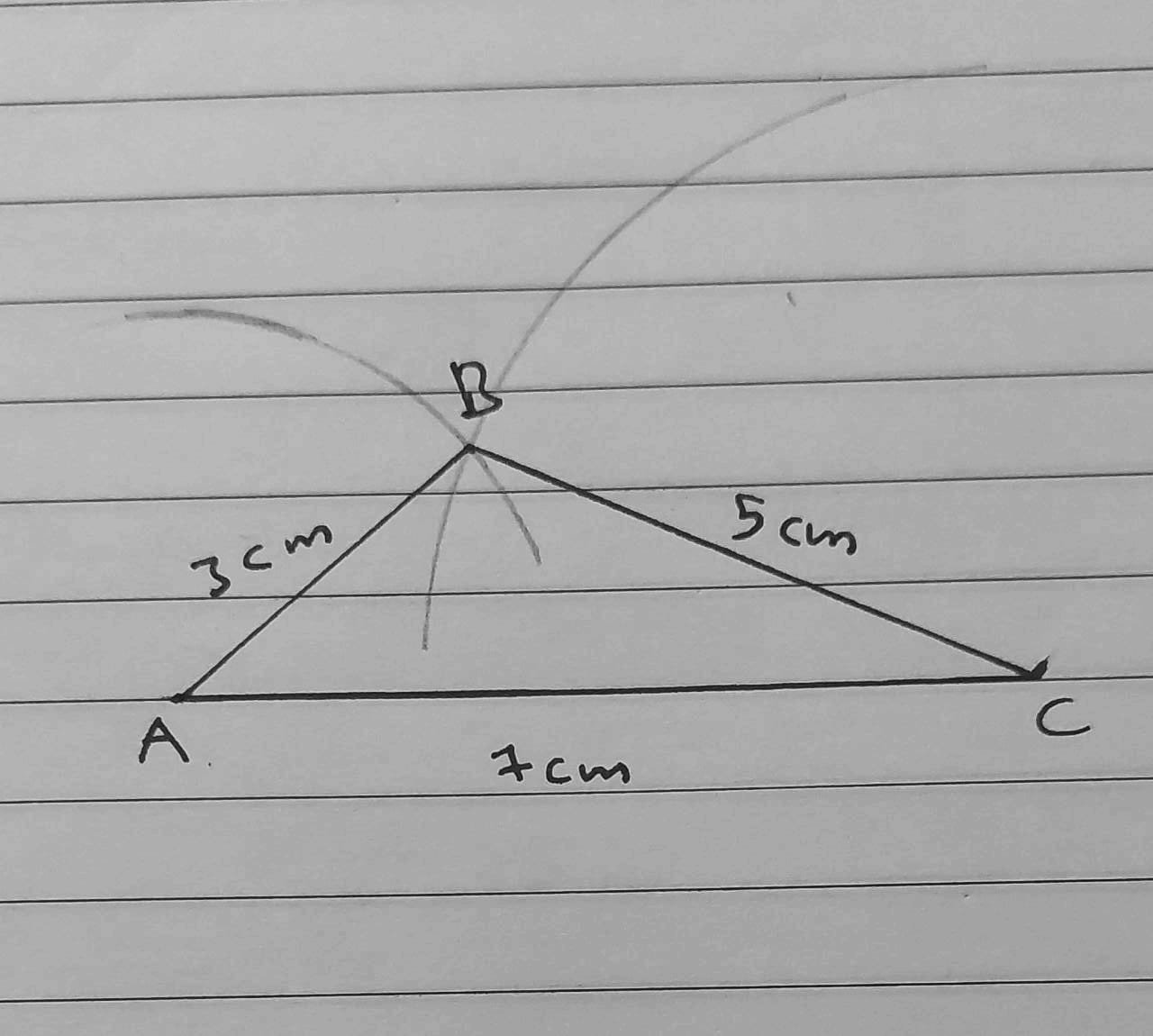
2) AB = 6 cm , BC = 4 cm , AC = 5 cm

---

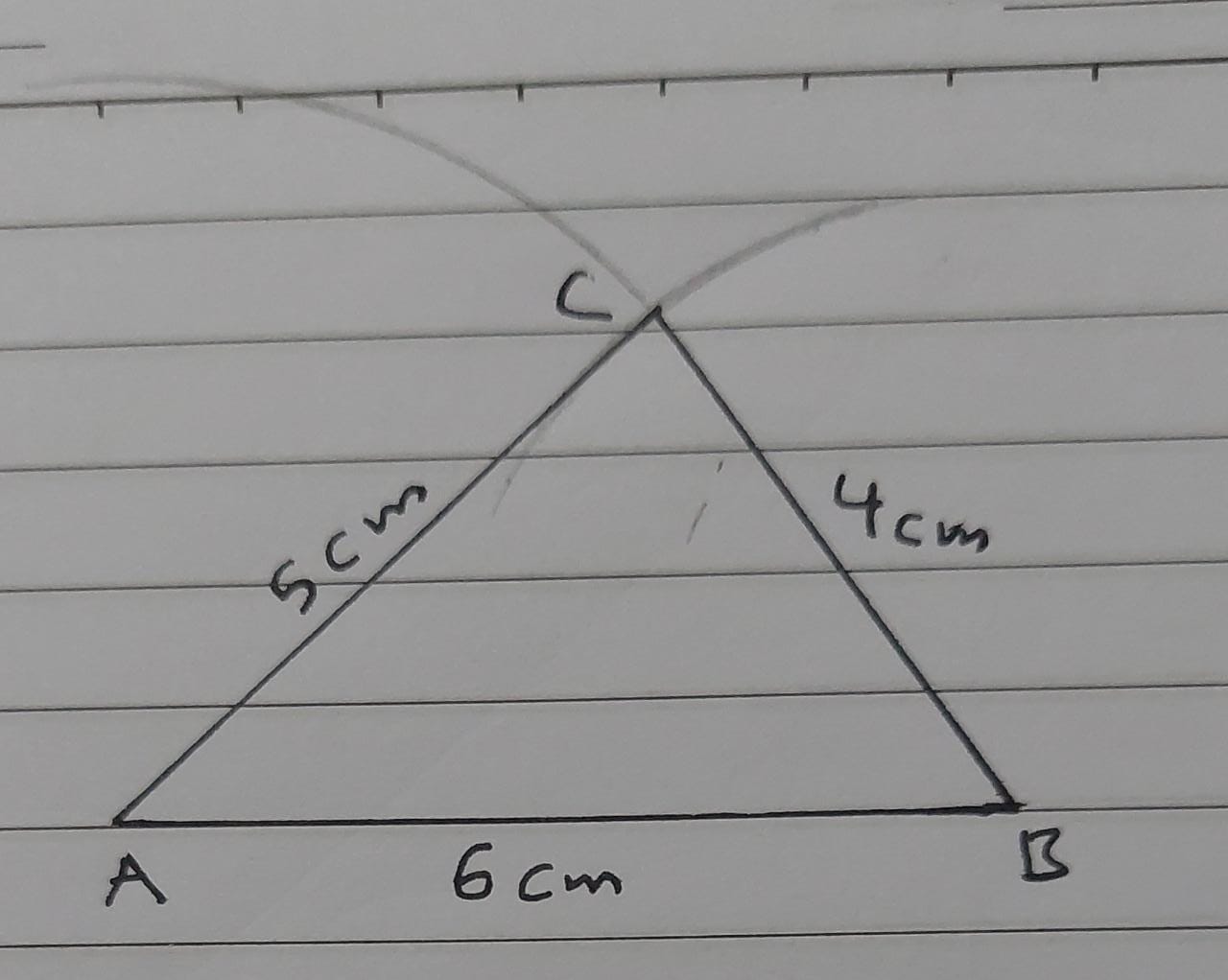
أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ لِرَسْمِ Δ ABC ، حيث : 

3)  AB = 6 cm , m∠CAB = 40°, m∠CBA = 60°

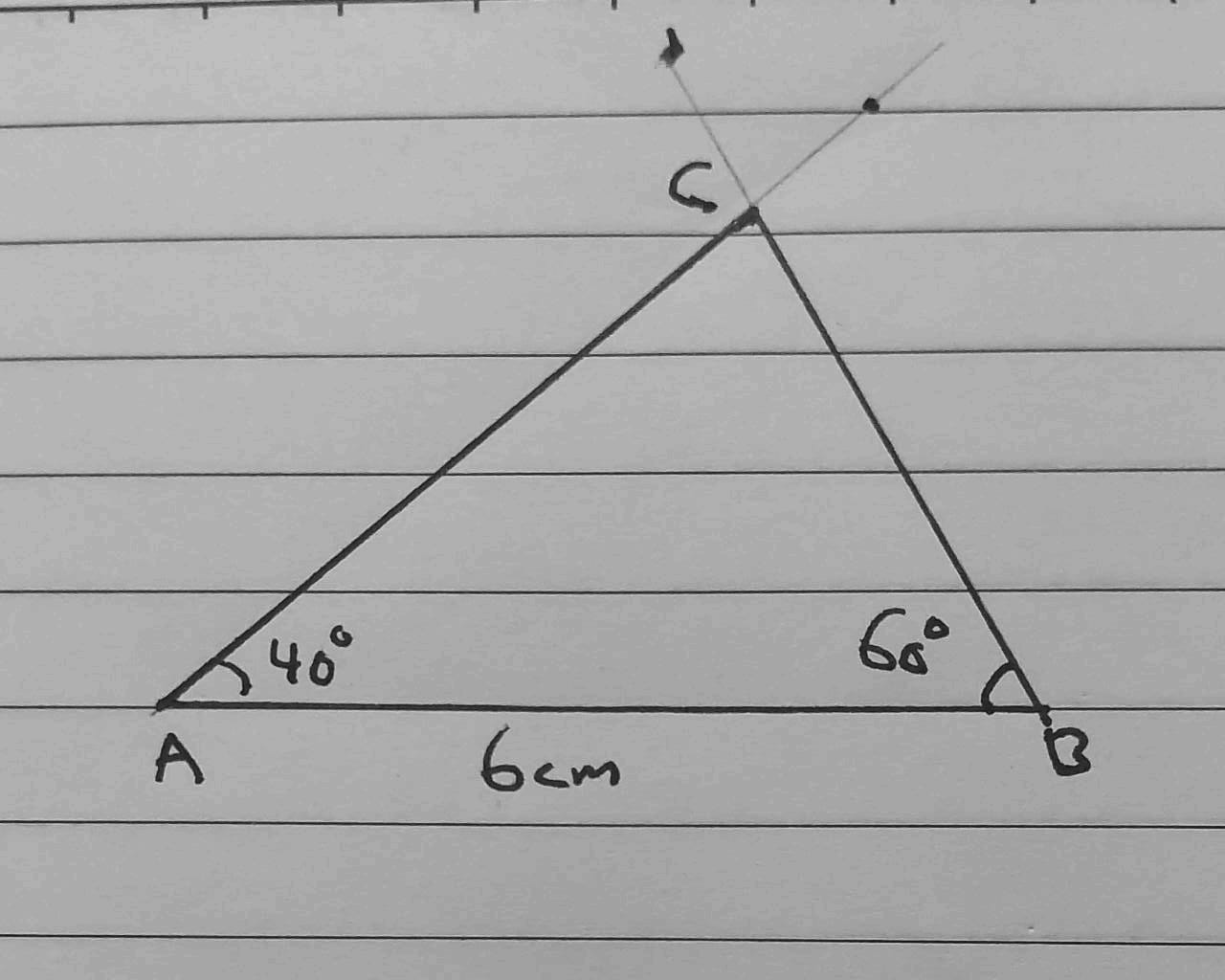
4) AB = 5 cm , m∠CAB = 30°, m∠CBA = 50°

---

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ وَالْفِرْجارَ لِرَسْمِ Δ ABC ، حيث : 

5) AB = 4 cm , AC = 6 cm , m∠BAC = 50°

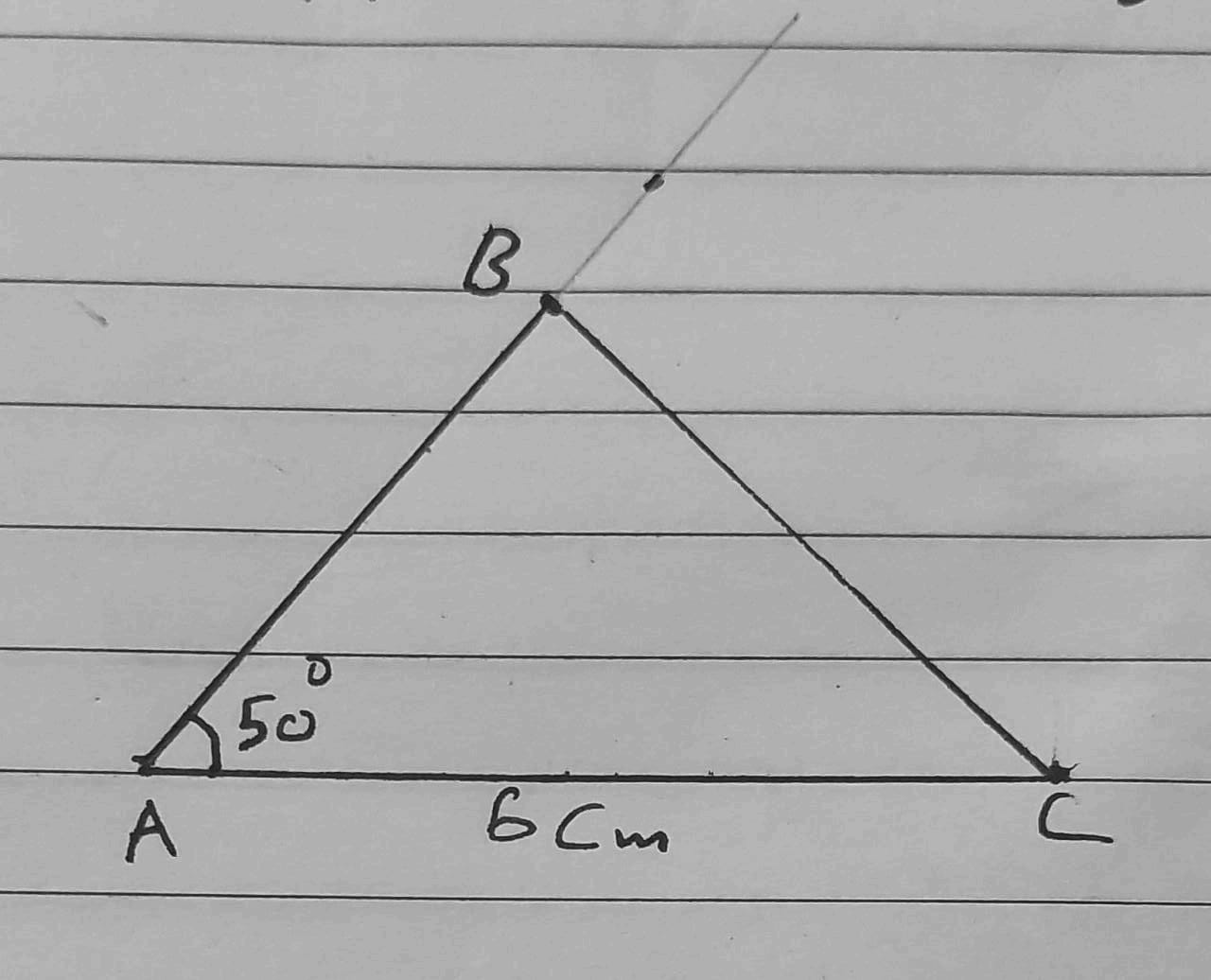
هنا استخدمنا المسطرة والمنقلة فقط لأن الزاوية المعلومة محصورة بين الضلعين المعلومين.

6) AB = 5 cm , AC = 4 cm , m∠BAC = 60°

 

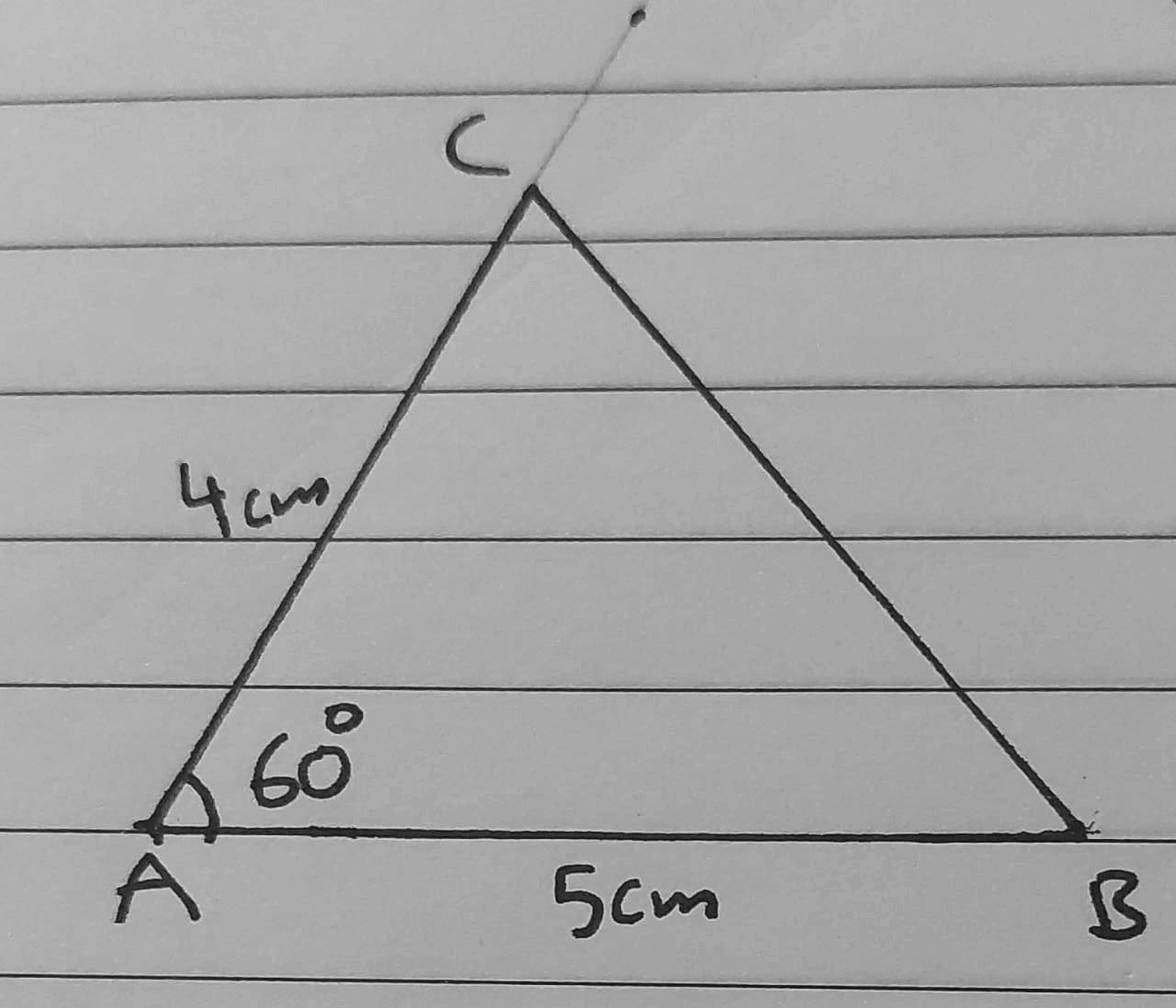
هنا استخدمنا المسطرة والمنقلة فقط لأن الزاوية المعلومة محصورة بين الضلعين المعلومين.

---

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ وَالْفِرْجارَ لِرَسْمِ Δ ABC ، حيث : 

7) AB = 5 cm , AC = 6 cm , m∠ABC = 35°

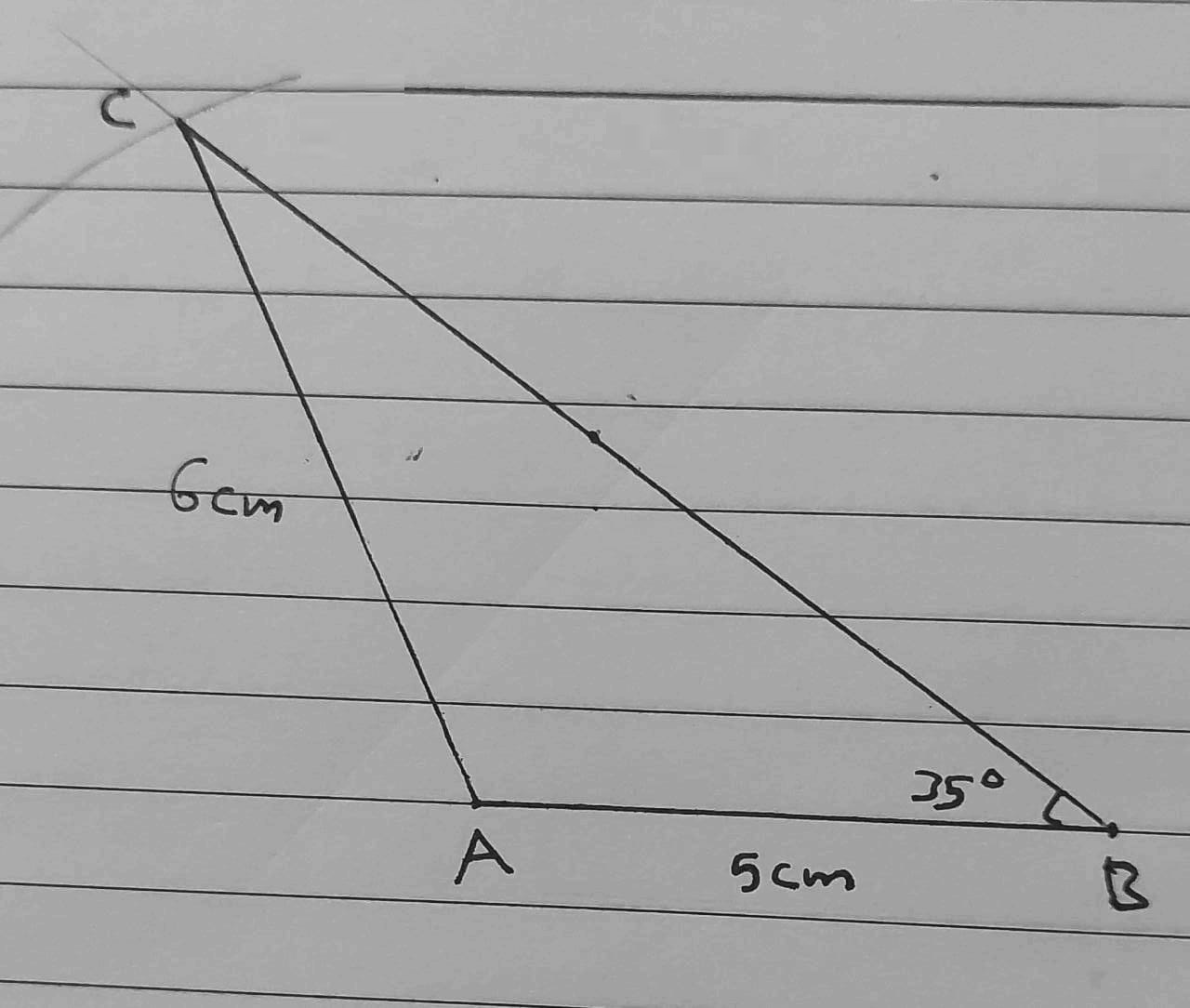
8) AB = 6 cm , AC = 4 cm , m∠ABC = 40°

---

 

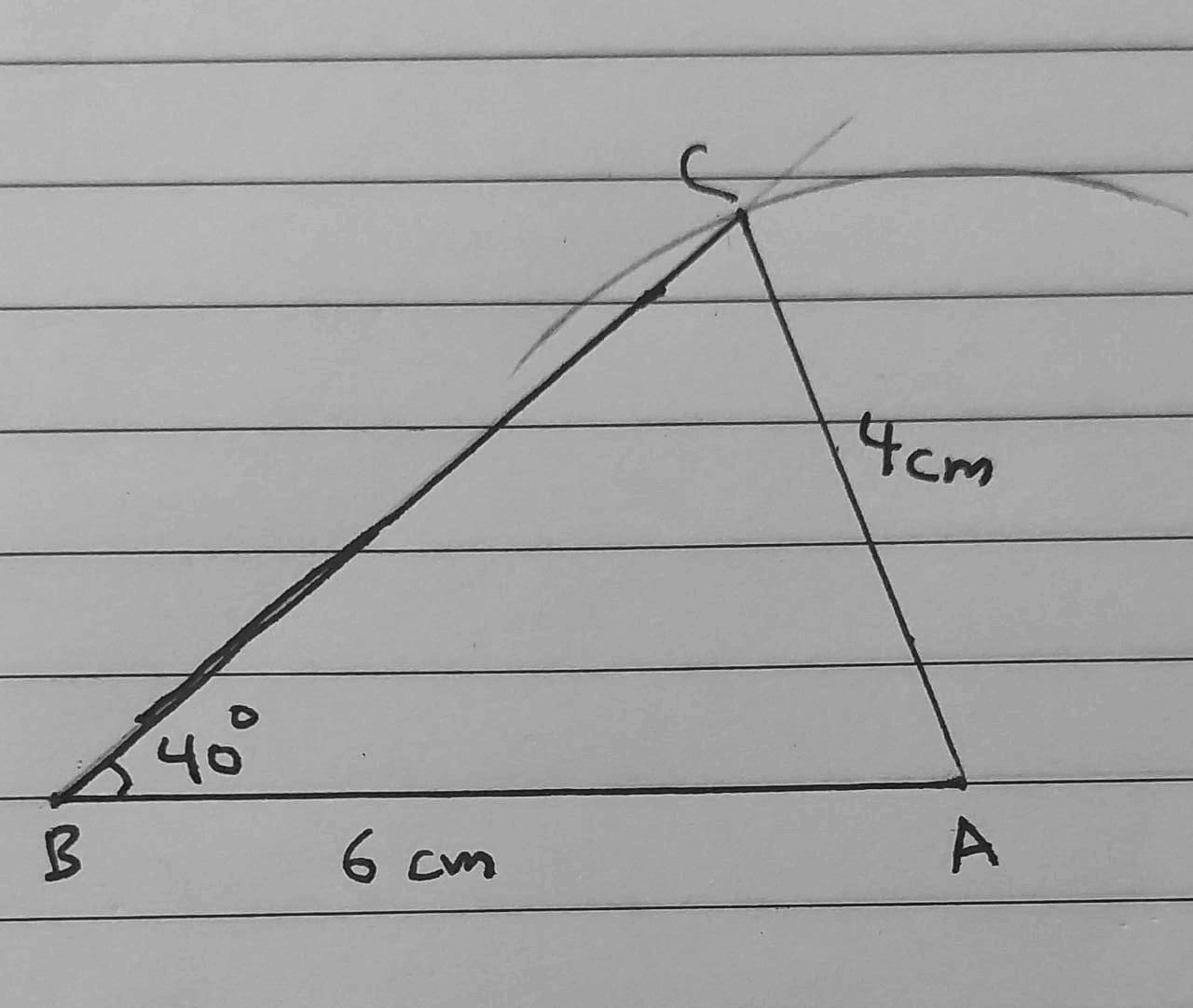
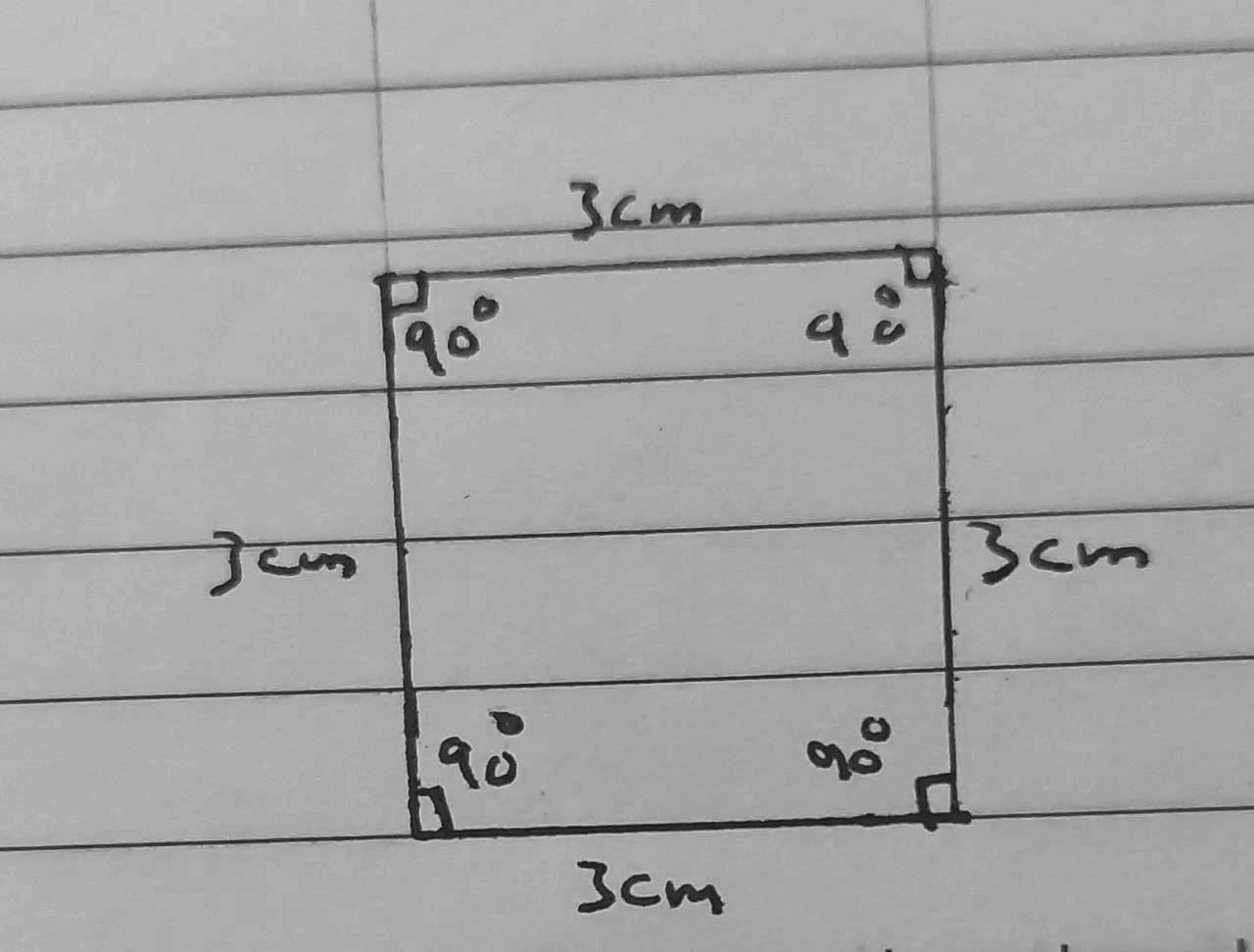
9) أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ لِرَسْمِ مُرَبَّعٍ، طولُ ضِلْعِهِ 3cm

الحل : 

زوايا المربع متساوية وقياس كل منها 90ْ

---

 

أَرْسُمُ بِدِقَّةٍ Δ ABC ، حيث : $AB = 8 cm , BC = 5.5 cm , AC = 4 cm$  ، ثُمَّ أَرْسُمُ عَلى الشَّكْلِ نَفْسِهِ: 

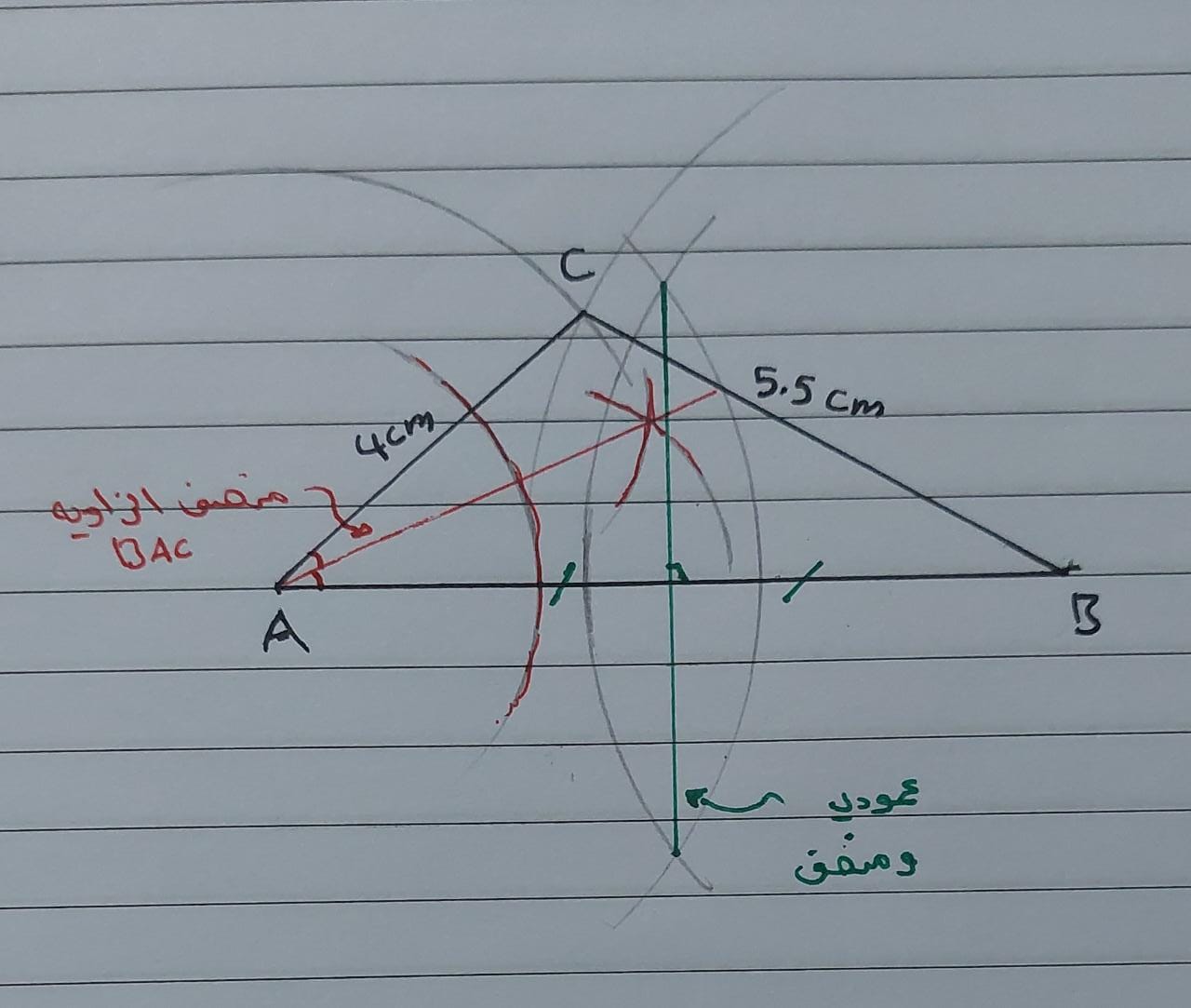
10) مُنَصِّفَ الزّاوِيَةِ BAC

11) الْمُنَصِّفَ الْعَمودِيَّ لِلْقِطْعَةِ الْمُسْتَقيمَةِ AB

الحل : 

 

---

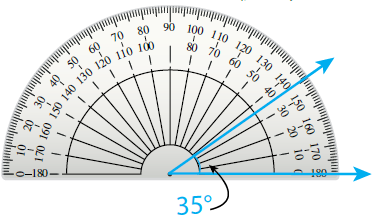
12) أَكْتَشِفُ الْخَطَأَ : أَرادَتْ مَنارُ رَسْمَ مُثَلَّثٍ، فَبَدَأَتْ بِرَسْمِ إِحْدى زَواياهُ كَما في الشَّكْلِ التّالي. قالَتْ لَها زَميلَتُها سُنْدُسُ: إِنَّكِ تَرْسُمينَ مُثَلَّثًا حادَّ الزَّوايا. هَلْ ما قالَتْهُ سُنْدُسُ صَحيحٌ؟ أَرْسُمُ مُثَلَّثًا لُِأبَرِّرَ إِجابَتي.

الحل : 

خطأ؛ قد يكون في المثلث زاوية أخرى قائمة أو منفرجة.

---

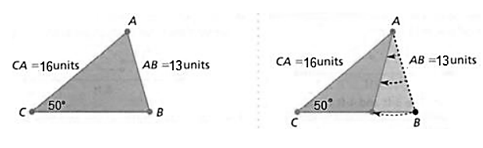
13) تَبْريرٌ : مُثَلَّثانِ مُخْتَلِفانِ، يَشْتَرِكانِ في طولَيْ ضِلْعَيْنِ، أَحَدُهُما طولُهُ 13 وَحْدَةً، وَالْآخَرُ طولُهُ 16 وَحْدَةً، وَقِياسُ زاوِيَةٍ غَيْرُ مَحْصورَةٍ بَيْنَهُما ° 50 ، أَرْسُمُ مُثَلَّثَيْنِ يُحَقِّقانِ الْمَطْلوبَ، ثُمَّ أُحَدِّدُ نَوْعَ كُلٍّ مِنْهُما، مُبَرِّرًا إِجابَتي.

الحل : 

---

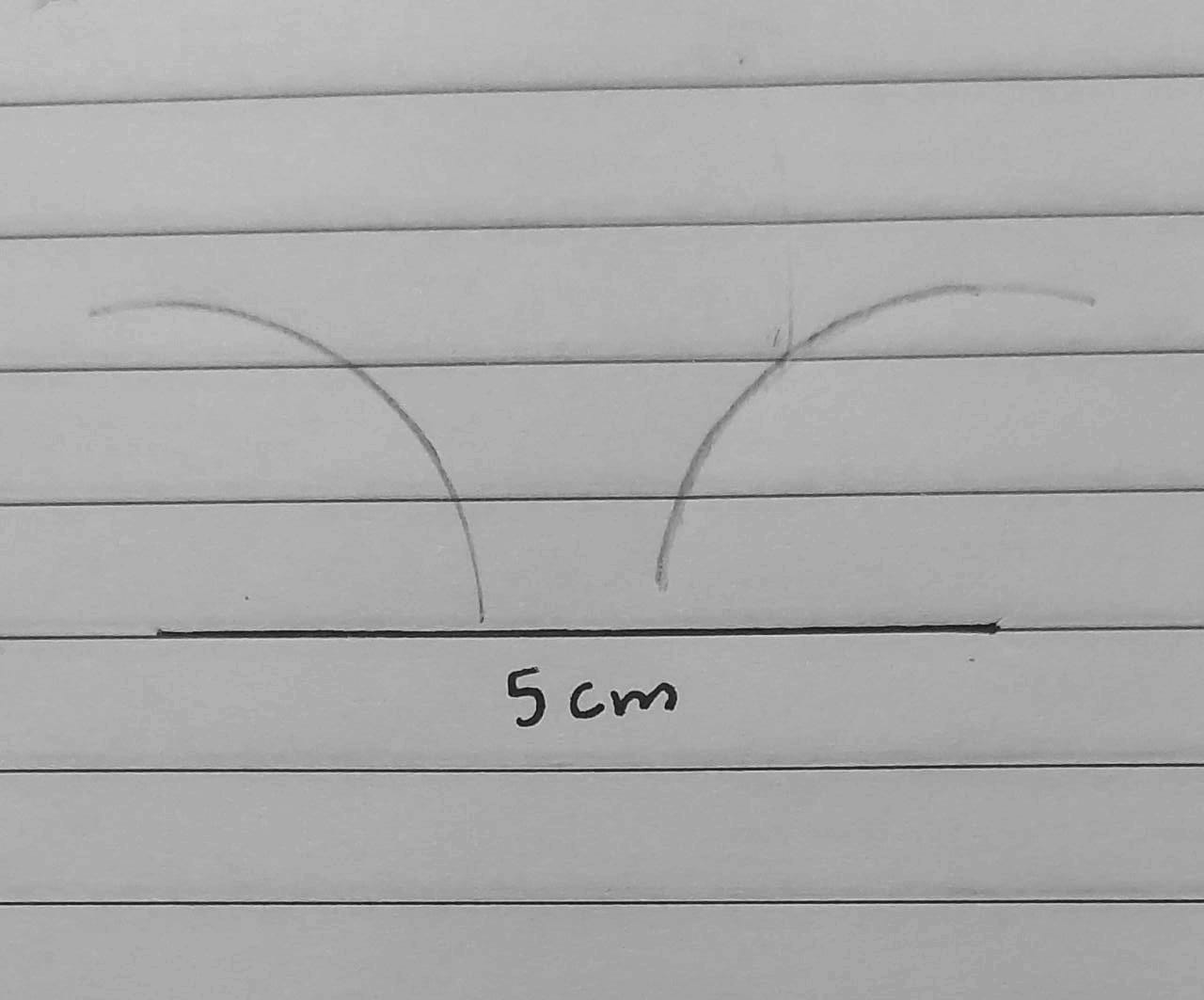
14) تَحَدٍّ: أَرْسُمُ مُثَلَّثًا أَطْوالُ أَضْلاعِهِ  $5 cm , 2 cm , 2 cm$ إنِْ أمَْكَنَ. وَإذِا تَعَذَّرَ عَلَيَّ ذلِكَ فَأُبَرِّرُ إِجابَتي.        

الحل : 

لا يمكن؛ لأن مجموع ضلعين فيه ليس أكبر من الضلع الثالث.

---

مَسْأَلَةٌ مَفْتوحَةٌ: أَرْسُمُ الْمُثَلَّثَ في كُلٍّ مِمّا يَأْتي بِحَسَبِ الزَّوايا الْمُعْطاةِ إِنْ أَمْكَنَ:

15) 45°, 45°, 90°

$45°+ 45°+ 90°=180°$ يُمكن رسم المثلث لأن مجموع الزاويا

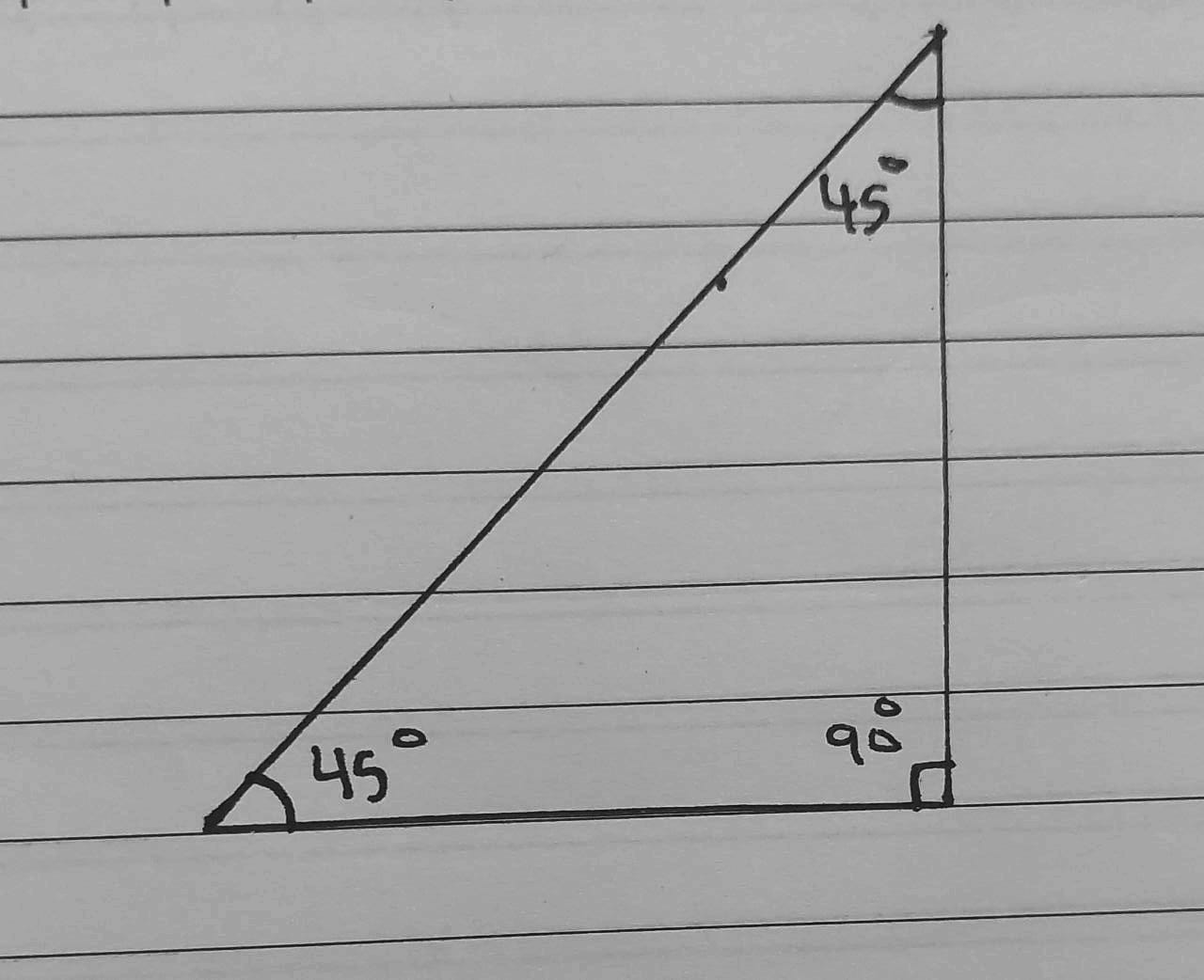
16) 100°, 55°, 25°

$100°,+ 55°+ 25°=180°$ يُمكن رسم المثلث لأن مجموع الزاويا

17) 60°, 60° , 80°

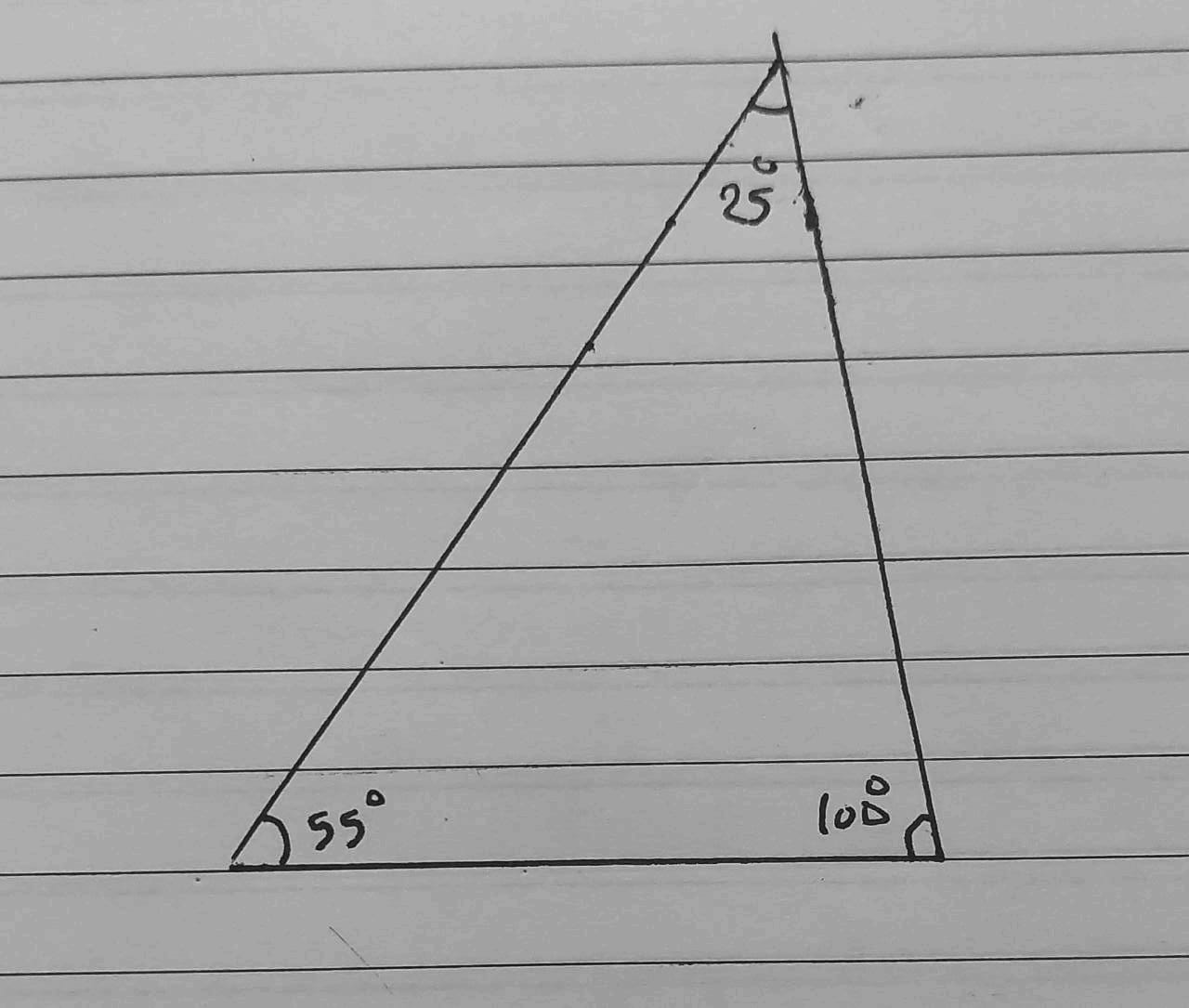
$60°, 60° , 80°=200°$ 

لا يُمكن رسم المثلث لأن مجموع الزاويا لا يساوي 180

---

أسئلة كتاب التمارين

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْفِرْجارَ لِرَسْمِ ΔABC في كُلٍّ مِنَ الْحالاتِ الْآتِيَةِ:

1) AB = 8 cm, BC = 5 cm, AC = 12 cm 

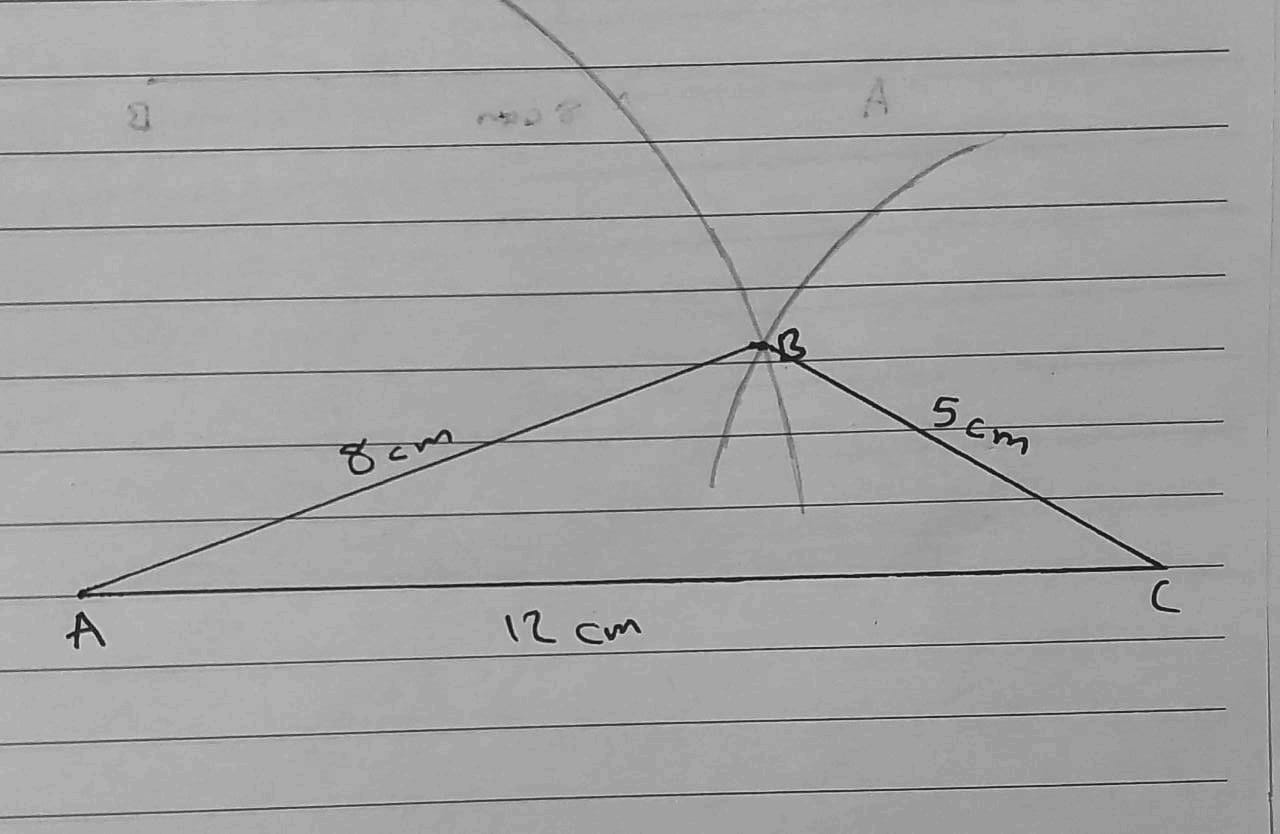
2) AB = 4 cm, BC = 9 cm, AC = 10 cm

---

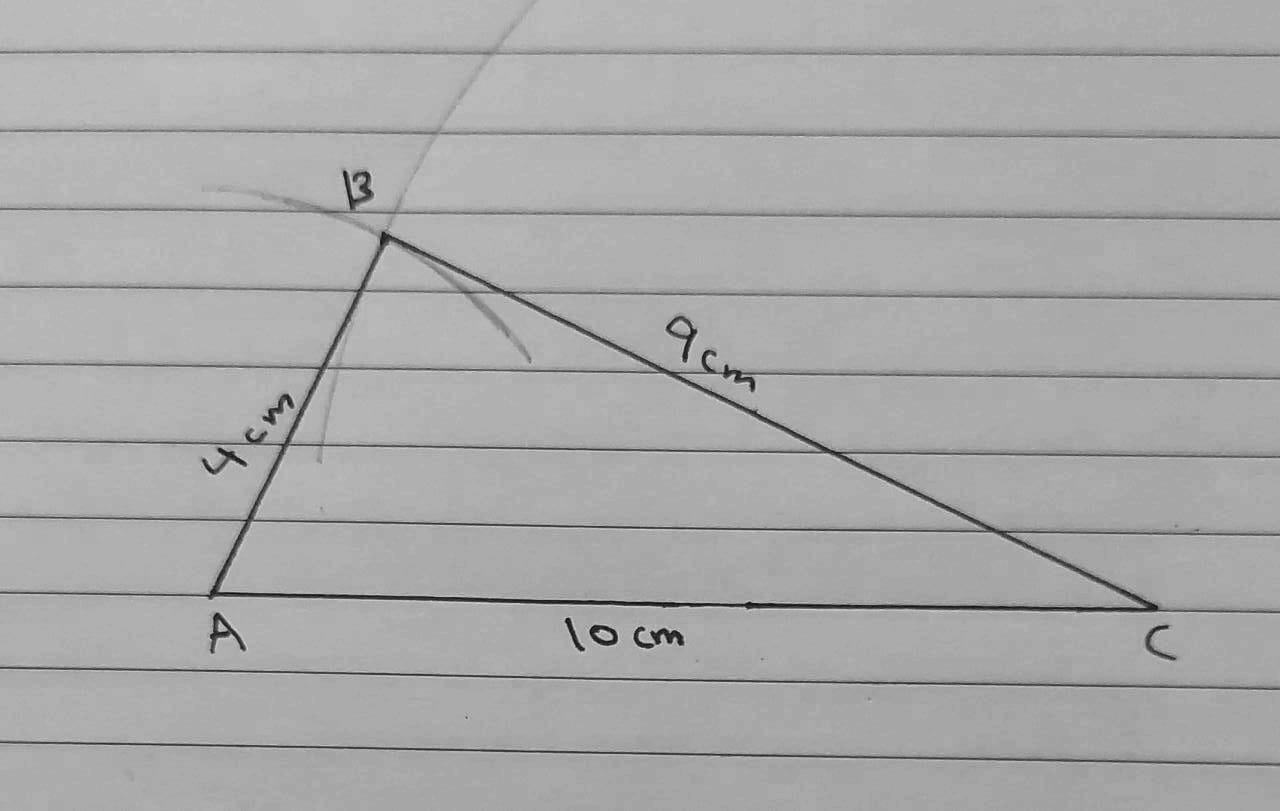
أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ لِرَسْمِ ΔABC في كُلٍّ مِنَ الْحالاتِ الْآتِيَةِ:

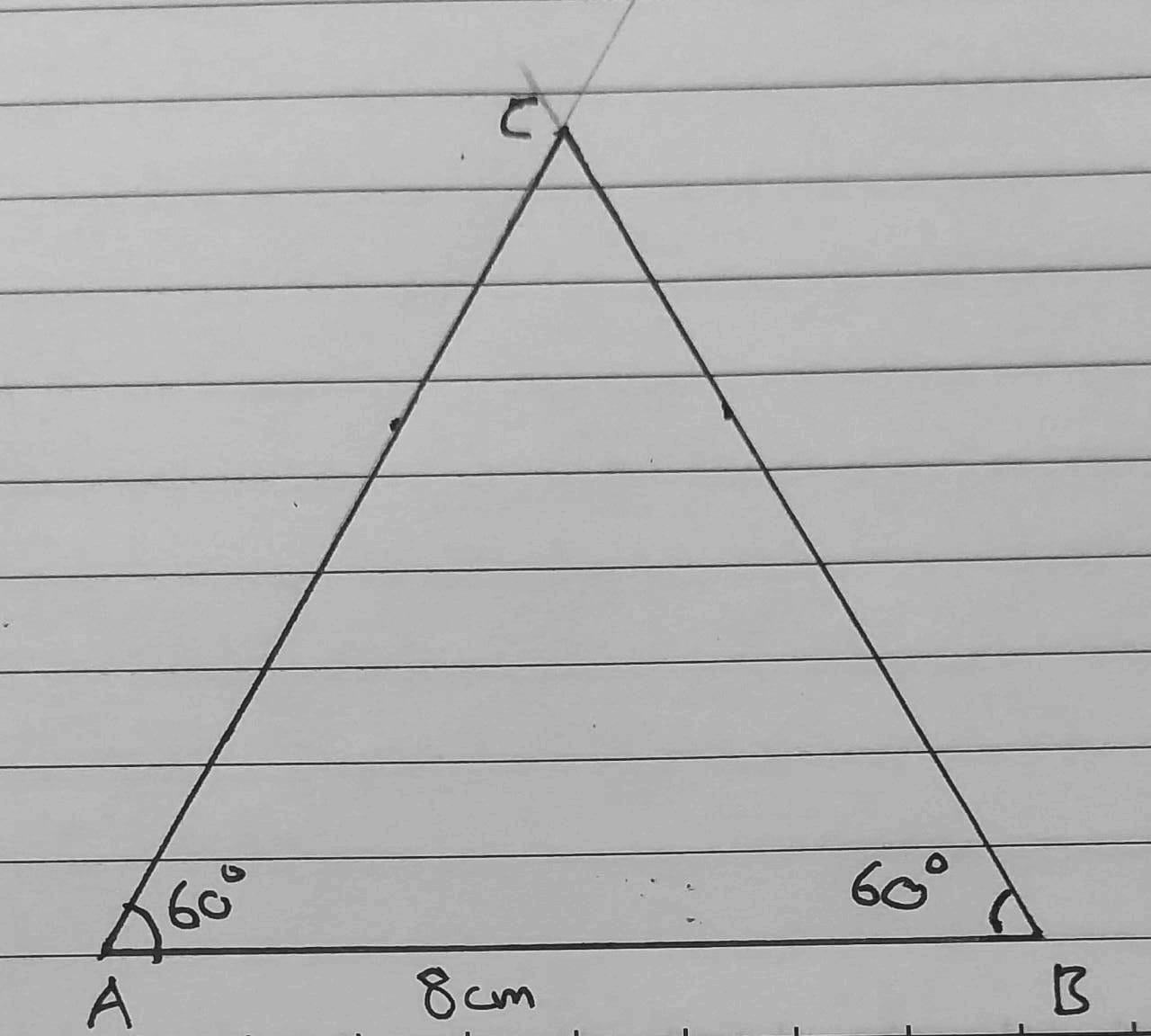
3) AB = 8 cm, m∠CAB = 60°, m∠CBA = 60°

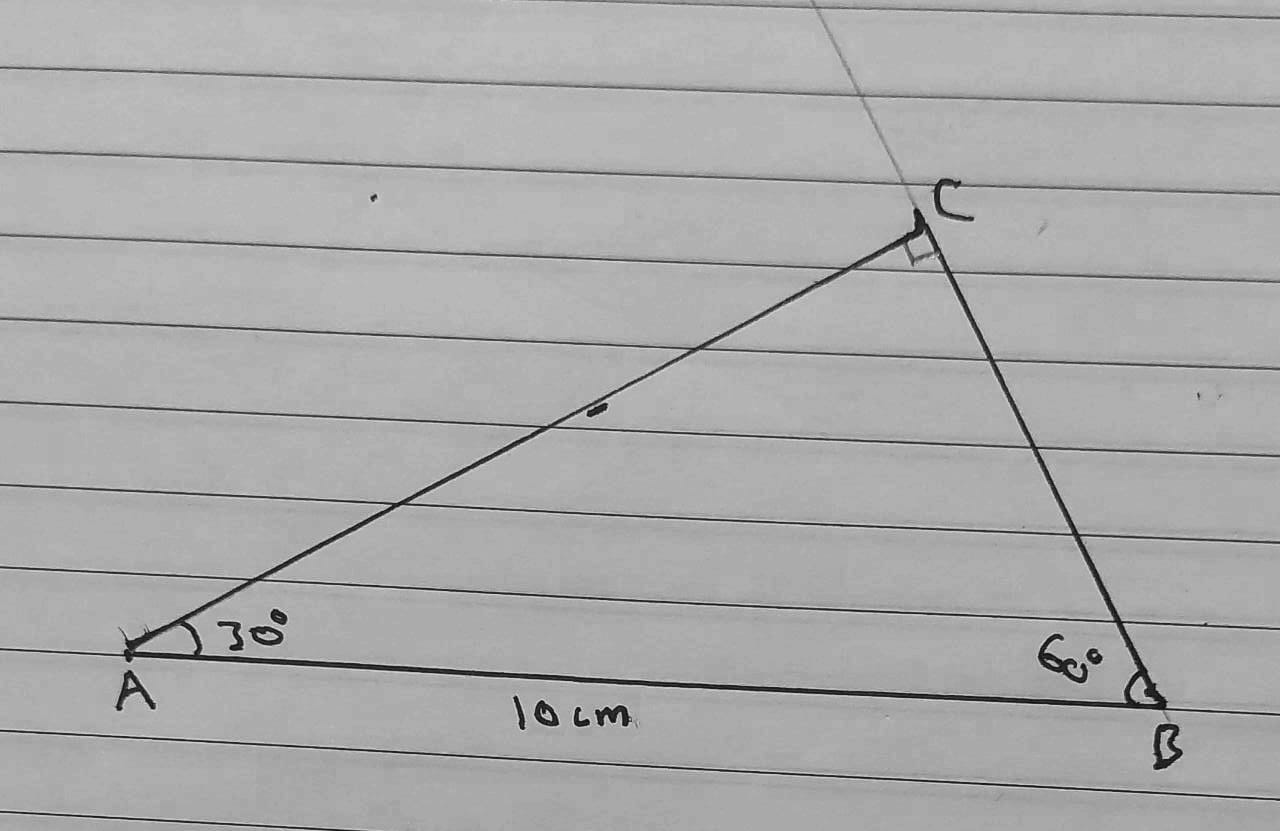
4) AB = 10 cm, m∠CAB = 30°, m∠CBA = 60°

---

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ والفرجار لِرَسْمِ ΔABC في كُلٍّ مِنَ الْحالاتِ الْآتِيَةِ:

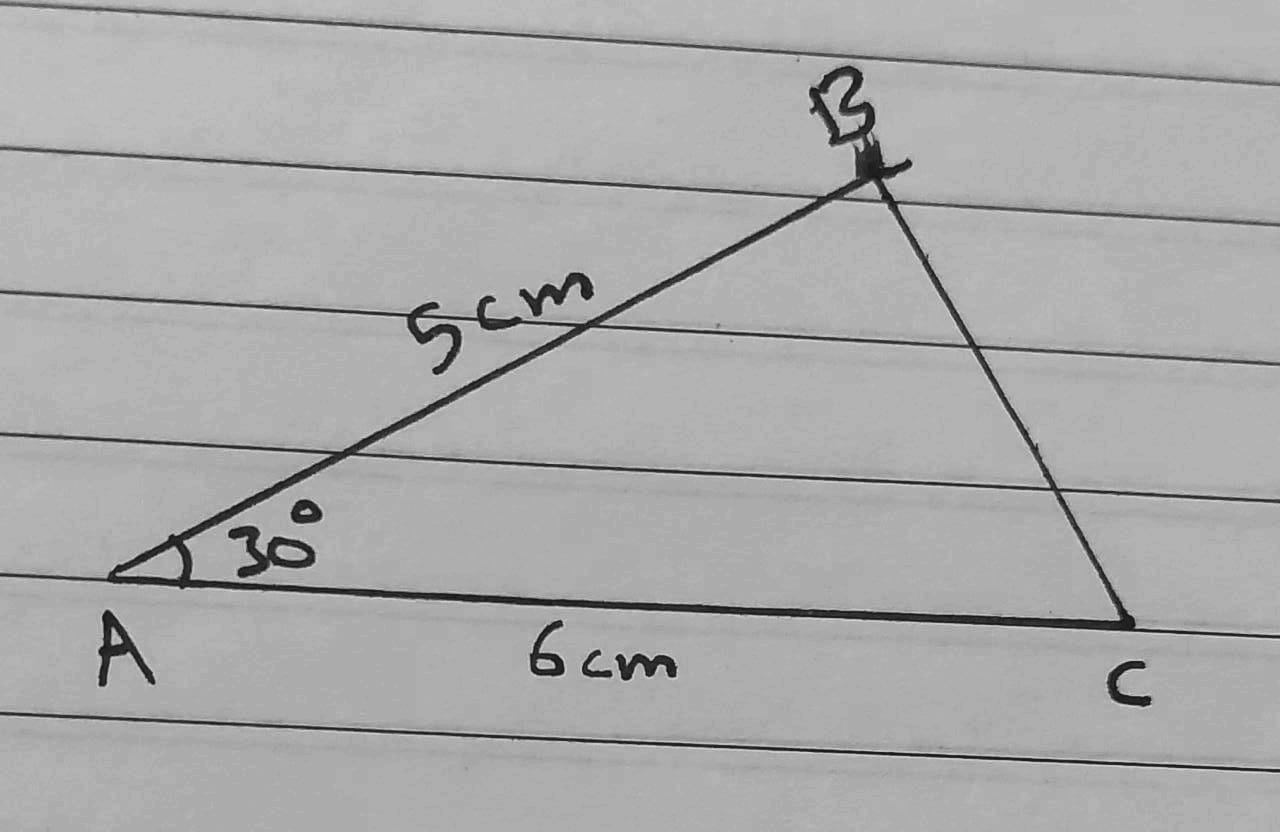
5) AB = 5 cm, AC = 6 cm, m∠BAC = 30°

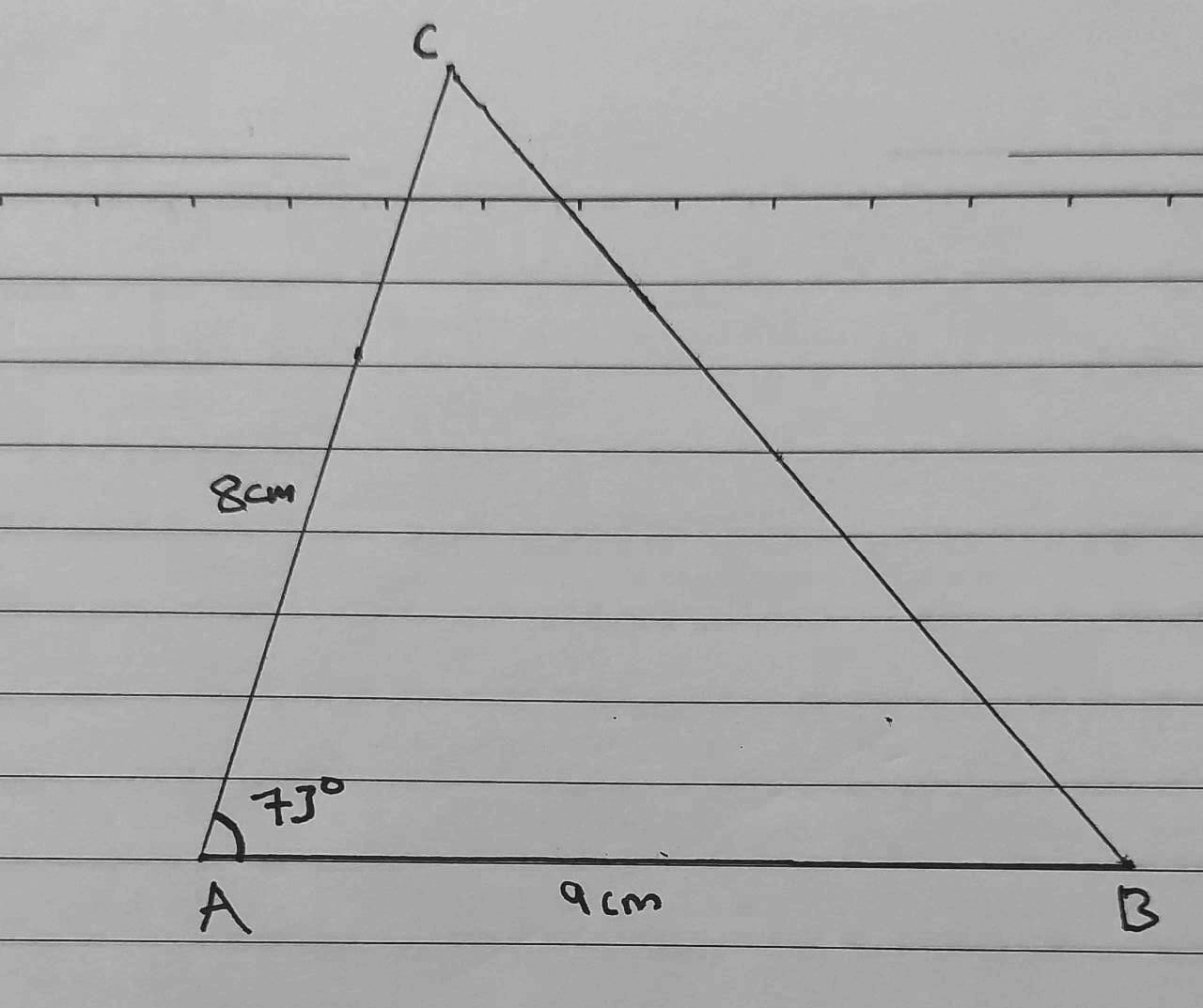
6) AB = 9 cm, AC = 8 cm, m∠BAC = 73°

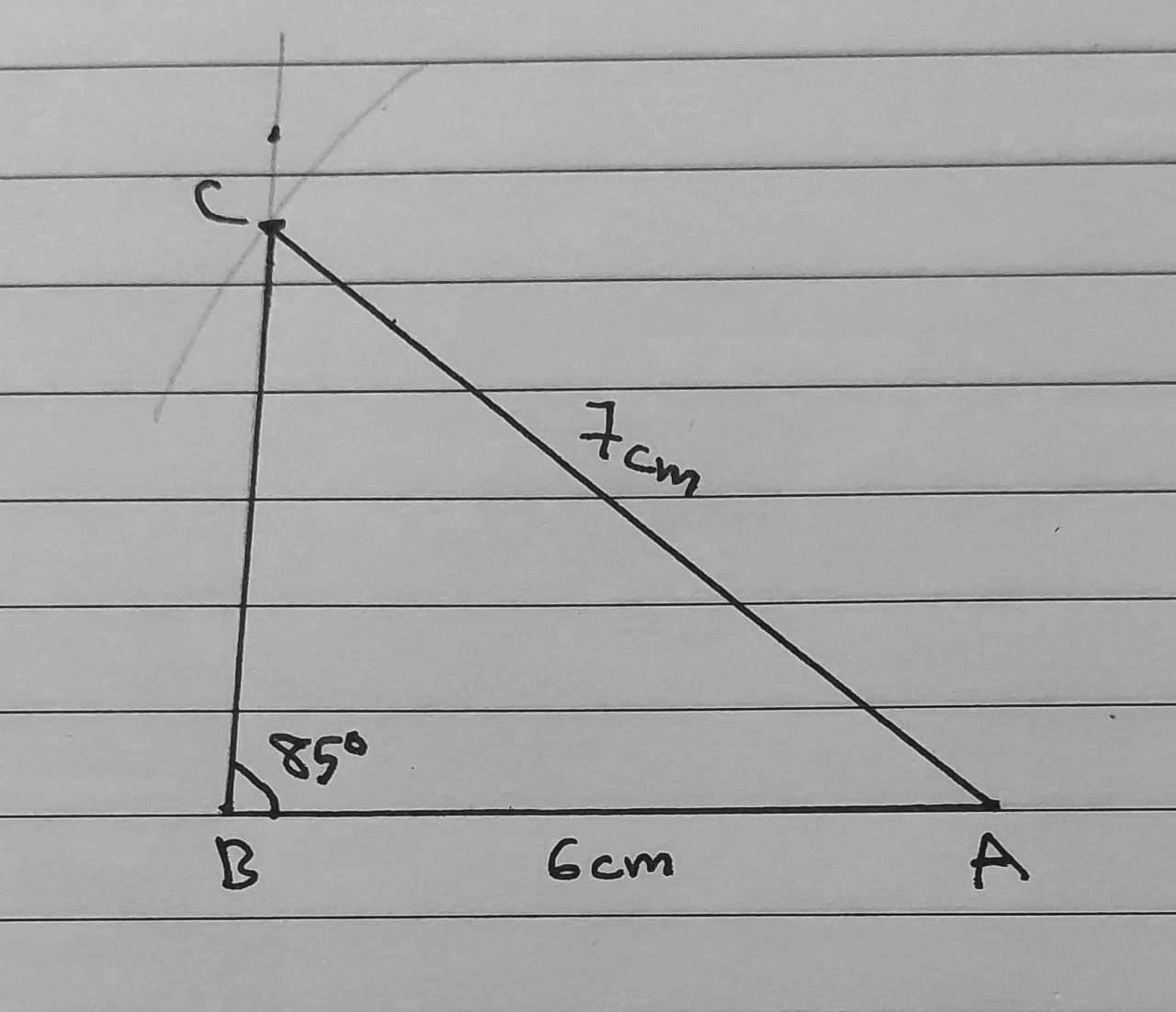
7) AB = 6 cm, AC = 7 cm, m∠ABC = 85°

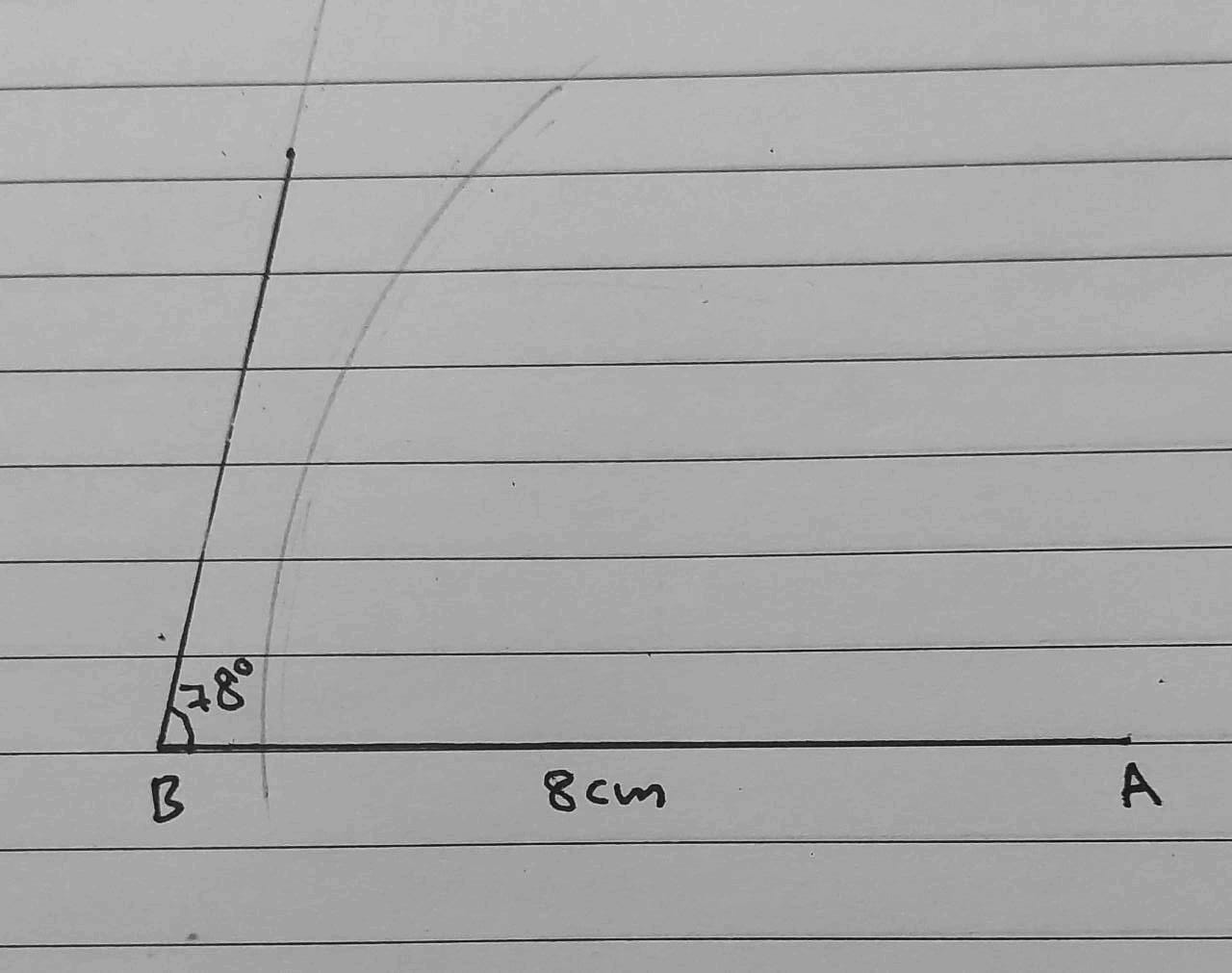
8) AB = 8 cm, AC = 7 cm, m∠ABC = 78°

لا يُمكن رسم هذا المثلث.

---

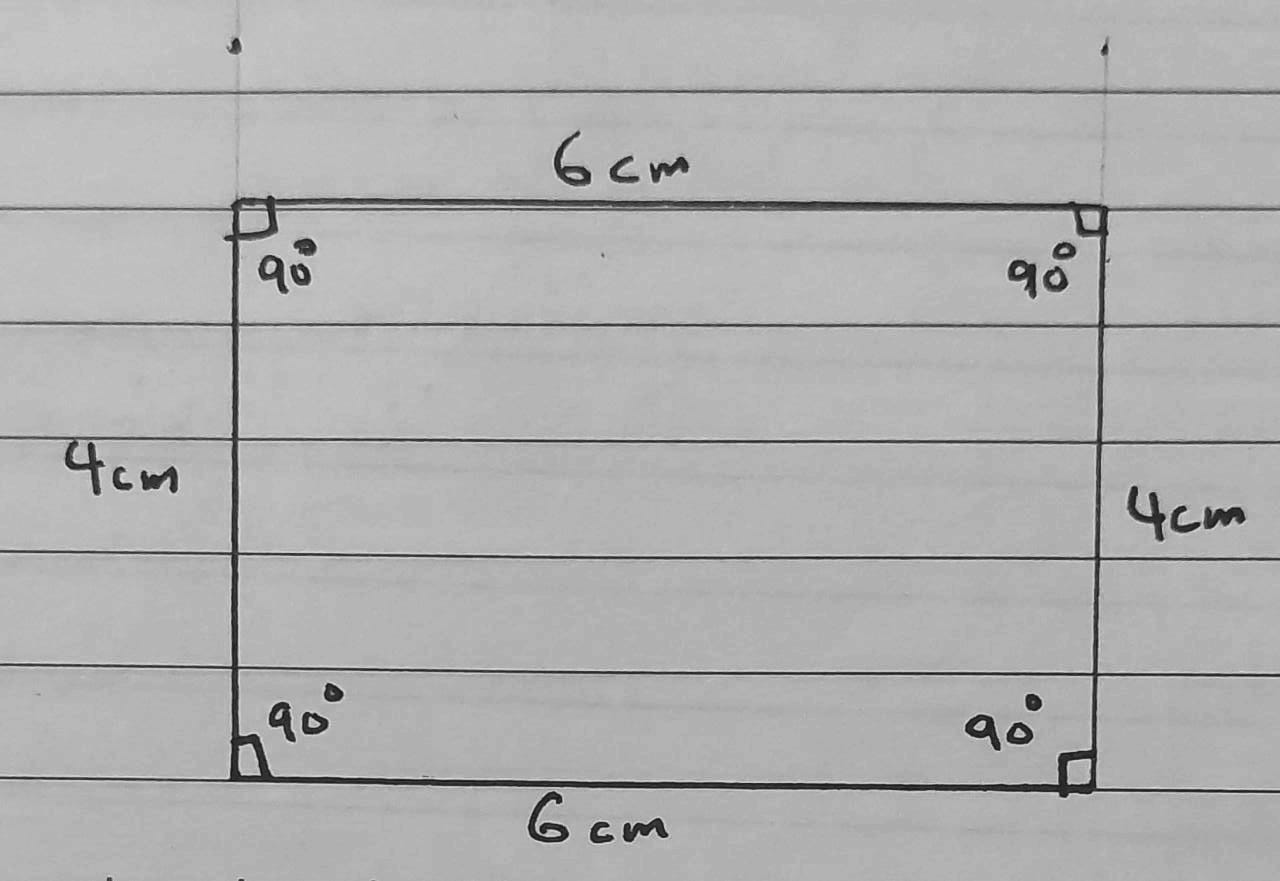
9) أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمِنْقَلَةَ لِرَسْمِ مُسْتَطيلٍ، طولُ ضِلْعَيْنِ فيهِ $6 cm , 4 cm$  

الحل : 

---

أُسَمّي مُعْطَياتِ حالَةِ رَسْمِ كُلِّ مُثَلَّثٍ مِمّا يَأْتي (أَطْوالُ ثَلاثَةِ أَضْلاعٍ، قِياسُ زاوِيَتَيْنِ وَطولُ ضِلْعٍ مَحْصورٍ بَيْنَهُما، طولُ ضِلْعَيْنِ
وَقِياسُ زاوِيَةٍ مَحْصورَةٍ بَيْنَهُما، طولُ ضِلْعَيْنِ وَقِياسُ زاوِيَةٍ غَيْرِ مَحْصورَةٍ بَيْنَهُما):

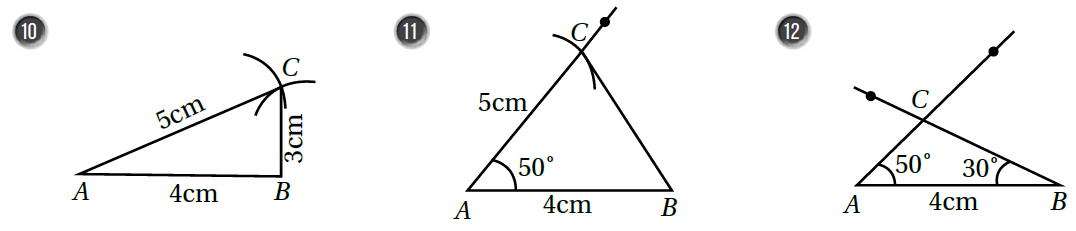
الحل: 

10) أطوال ثلاثة أضلاع.

11) طول ضلعين وقياس زاوية محصورة بينهما.

12) قياس زاويتين وطول ضلع محصور بينهما.