مفهوم أساسي :
عندما أضربُ عددًا في حدٍّ جبريٍّ، فإنَّني أجدُ ناتجَ ضربِ العددِ في معامِلِ الحدِّ الجبريِّ، ثمَّ أضعُ الناتجَ جانبَ المتغيّرِ.
| 2z | 2z | 2z | 2z | ||||
| z | z | z | z | z | z | z | z |
| 8z | |||||||
يمكنُني تطبيقُ قواعدِ الأسسِ لضربِ حدٍّ جبريٍّ في آخرَ حتى لوِ اختلفَتْ مُتغيِّراتُهُما.
مثال1: أجدُ ناتجَ ضربِ الحدودِ الجبريَّةِ في كلٍّ ممّا يأتي:
1)
أضربُ العددَ 5- في معامِلِ الحدِّ (3)
2)
الخاصيُّة التبديليّةُ والتجميعيّةُ في الضربِ
قاعدةُ ضربِ القوى
3)
الخاصيُّة التبديليّةُ والتجميعيّةُ في الضربِ
قاعدةُ ضربِ القوى
4)
الخاصيُّة التبديليّةُ والتجميعيّةُ في الضربِ
قاعدةُ ضربِ القوى
يمكنُني ضربُ حدٍّ جبريٍّ في مقدارٍ جبريٍّ باستخدامِ خاصيّةِ التوزيعِ؛ وذلكَ بضربِ الحدِّ في كلِّ واحدٍ منْ حدودِ المقدارِ.
مثال2: أُبسِّطُ كلَّ مقدارٍ جبريٍّ ممّا يأتي، ثمَّ أجدُ قيمتَهُ عندَ القِيَمِ المُعطاةِ:
1)
أضربُ حدًّا جبريًّا في مقدارٍ جبريٍّ
أعوض x=3 , y=-7
أطبِّقُ أولويّاتِ العمليّاتِ
2)
أضربُ حدًّا جبريًّا في مقدارٍ جبريٍّ
أعوض x=-1,y=5
أطبِّقُ أولويّاتِ العمليّاتِ
يمكنُني أنْ أضربَ مقداريْنِ جبريَّيْنِ باستخدامِ نماذجِ المساحةِ، أوْ باستخدامِ خاصيَّةِ التوزيعِ؛ وذلكَ بضربِ كلِّ حدٍّ منْ حدودِ المقدارِ الأولِ في كلِّ حدٍّ منْ حدودِ المقدارِ الثاني.
مثال 3 : أجدُ ناتجَ الضربِ في أبسطِ صورةٍ.
الطريقةُ 1: نماذجُ المساحةِ.
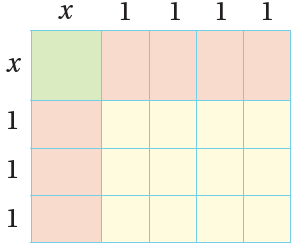
طولُ المستطيلِ الكبيرِ وحداتٍ، وعرضُهُ وحداتٍ.
مساحةُ المستطيلِ الكبيرِ تساوي ناتجَ ضربِ المقدارينِ الجبريَّينِ.
مساحةُ المربّعِ الأخضرِ تساوي وحدةً مربَّعَةً.
مساحةُ كلِّ واحدٍ منَ المستطيلاتِ الحمراءِ تساوي وحدةً مربَّعَةً.
مساحةُ كلِّ واحدٍ منَ المربَّعاتِ البرتقاليّةِ تساوي وحدةً مربَّعَةً. .
إذنْ، مساحةُ المستطيلِ الكبيرِ، هيَ ناتج جمع مساحات الأشكال المكونة له:
الطريقةُ 2: خاصيَّةُ التوزيعِ.
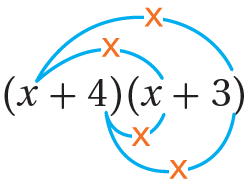 |
يمكنُني أيضًا استخدامُ خاصيّةِ التوزيعِ بطريقةٍ مختلفةٍ كما يأتي:
أفصلُ المقدارَ (x+4) إلى حدَّيْنِ x,4 ثم أضربُ كلًّ منْهُما في المقدارِ (x+3)
أستخدمُ خاصيَّةَ التوزيعِ
أجمعُ الحدودَ المتشابهةَ
أكتبُ المقدارَ في أبسطِ صورةٍ
يمكنُني استخدامُ ضربِ المقاديرِ الجبريّةِ في التطبيقاتِ الحياتيّةِ.
مثال 4: منَ الحياةِ: ملعبٌ مستطيلُ الشكلِ، طولُهُ وعرضُهُ يُرادُ زراعتُهُ بالنجيلِ. أجدُ مساحةَ المنطقةِ المزروعةِ بالنجيلِ بدلالةِ x
A=L×W
أفصلُ المقدارَ (5x+4) إلى حدَّيْنِ
أستخدمُ خاصيَّةَ التوزيعِ
قاعدةُ ضربِ القوى في الأسسِ
الخاصيّةُ التجميعيّةُ
أجمعُ الحدودَ المتشابهةَ