فكرة الدرس:
- أضربُ عددين صحيحين، وأقسمُهُما.
- أستعملُ ترتيب العمليّات لإجراء عمليّاتٍ حسابيّةٍ بسيطةٍ.
تعلّم أنّ عمليّة الضّرب هي عمليّةُ جمعٍ مُتكرّرٍ. فمثلا:
يُمكنُ تمثيلُ الجمع المُتكرّر بقطع العدّ، وعلى خطّ الأعداد:
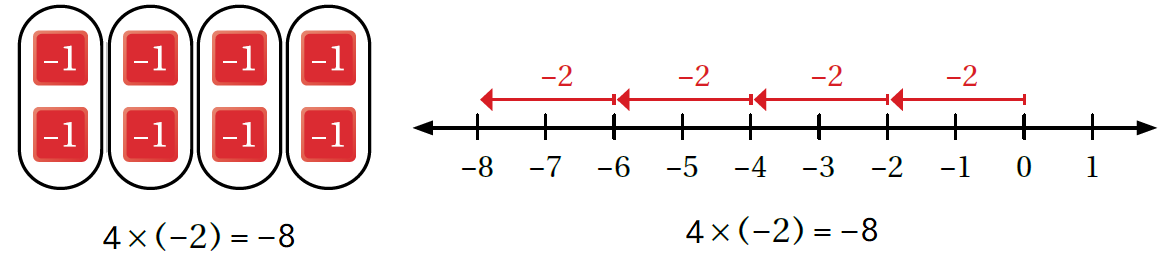
وبشكل عام: ناتج ضرب عددين صحيحين مُختلفين في الإشارة يكونُ سالبًا؛ أي إنّ:
| ناتج ضرب عددٍ سالبٍ في عددٍ موجبٍ يُساوي عددًا سالبًا |  |
| ناتج ضرب عددٍ موجبٍ في عددٍ سالبٍ يُساوي عددًا سالبًا |  |
مثال:
أجدُ ناتج كُلٍّ ممّا يأتي، ثُمّ أتحقّقُ من صحّة الحلّ باستعمال خطّ الأعداد:
| العددان مُختلفان في الإشارة. إذن، ناتجُ الضّرب سالبٌ |
| للتحقق: أستعملُ خطّ الأعداد. |
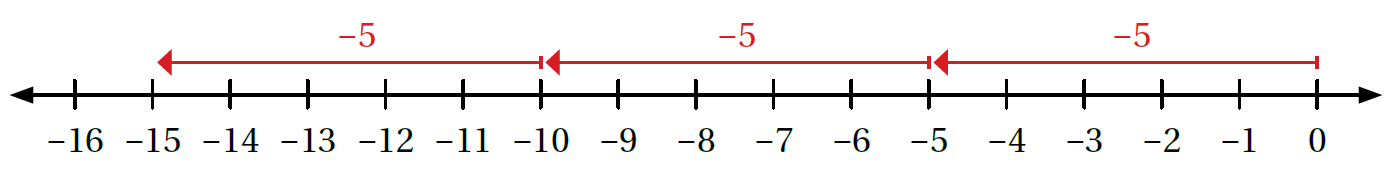 |
| العددان مُختلفان في الإشارة. إذن، ناتجُ الضّرب سالبٌ |
| للتحقق: أستعملُ خطّ الأعداد. |
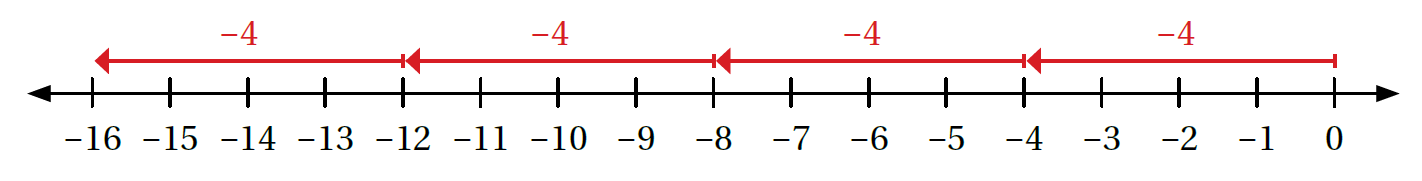 |
يُمكنُ استعمالُ معكوس ناتج ضرب عددين مُختلفين في الإشارة لإيجاد ناتج ضرب عددين مُتشابهين في الإشارة.
أتعلم: مَعْكوسُ هُوَ أو وَهُوَ أيضاً
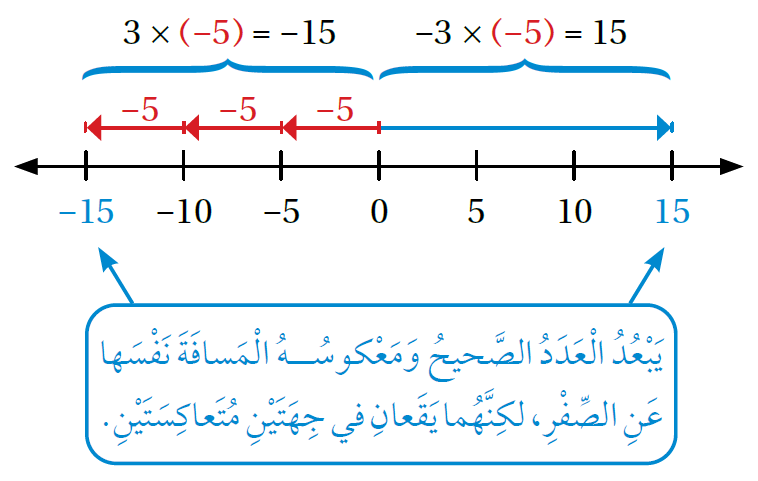
مثال آخر : معكوس هو وبما أنّ فيكون
وبشكل عام: ناتج ضرب عددين صحيحين مُتشابهين في الشارة يكونُ موجبًا؛ أي إنّ:
| ناتج ضرب عددٍ موجبٍ في عددٍ موجبٍ يُساوي عددًا موجبًا |  |
| ناتج ضرب عددٍ سالبٍ في عددٍ سالبٍ يُساوي عددًا موجبًا |  |
مثال:
أجدُ ناتج كُلٍّ ممّا يأتي:
| العددان لهُما الإشارةُ نفسُها. إذن، ناتجُ الضّرب موجبٌ |
| العددان لهُما الإشارةُ نفسُها. إذن، ناتجُ الضّرب موجبٌ |
| تعريف مربع العدد وناتج الضرب يكون موجب |
| خاصِّية التَّجميع |
| أَبدأُ العملِيّة داخلَ الأقواس |
يُمكنُ استعمالُ حقائق الضّرب والقسمة المُترابطة لإيجاد ناتج قسمة عددين صحيحين.
فمثلا، لإيجاد ناتج: ، أستعملُ حقائق الضّرب كما في المُخطّط الآتي:
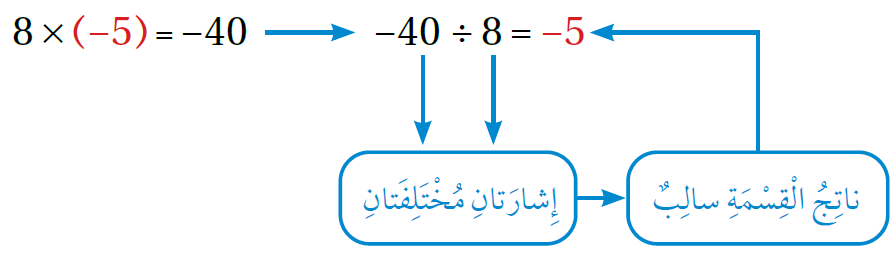
وبشكل عام: ناتج قسمة عددين صحيحين مُختلفين في الإشارة يكونُ سالبًا؛ أي إنّ:
| ناتج قسمة عددٍ سالبٍ على عددٍ موجبٍ يُساوي عددًا سالبًا |  |
| ناتج قسمة عددٍ موجبٍ على عددٍ سالبٍ يُساوي عددًا سالبًا |  |
مثال:
أجدُ ناتج كُلٍّ ممّا يأتي:
| العددان الصّحيحان مُختلفان في الإشارة. إذن، ناتجُ القسمة سالبٌ |
| العددان الصّحيحان مُختلفان في الإشارة. إذن، ناتجُ القسمة سالبٌ |
يُمكنُ أيضًا استعمالُ خصائص الضّرب والقسمة لإيجاد ناتج قسمة الأعداد الصّحيحة المُتشابهة في الإشارة، بحيثُ لا يكونُ المقسومُ عليه صفرًا. فمثلً، لإيجاد ناتج: ، أستعملُ حقائق الضّرب كما في الشّكل الآتي:
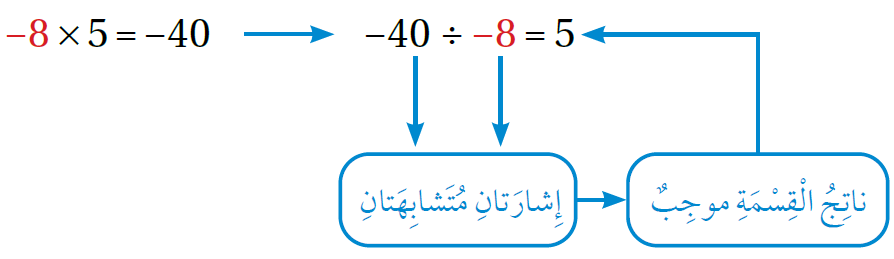
وبشكل عام: ناتج قسمة عددين صحيحين مُتشابهين في الإشارة يكونُ موجبًا؛ أي إنّ:
| ناتج قسمة عددٍ موجبٍ على عددٍ موجبٍ يُساوي عددًا موجبًا |  |
| ناتج قسمة عددٍ سالبٍ على عددٍ سالبٍ يُساوي عددًا موجبًا |  |
مثال:
أجدُ ناتج كُلٍّ ممّا يأتي:
| العددان لهُما الإشارةُ نفسُها. إذن، ناتجُ القسمة موجبٌ |
| العددان لهُما الإشارةُ نفسُها. إذن، ناتجُ القسمة موجبٌ |
| أَقسمُ أَولا |
| 4 أَضْرِبُ ناتِجَ الْقِسْمَةِ 4 في |
| أَبدأُ بِالعملِيَّةِ داخلَ الأقواس |
| أقسمُ أولا ثم أضرب 5 في ناتج القسمة |
مثال:
أسماكٌ: يُبيّنُ التّمثيلُ البيانيُّ المُجاورُ العُمق التّقريبيّ (بالأمتار) الّذي تعيشُ فيه بعضُ الأسماك. أجدُ مُعدّل الوسط الحسابيّ لهذه الأعماق.
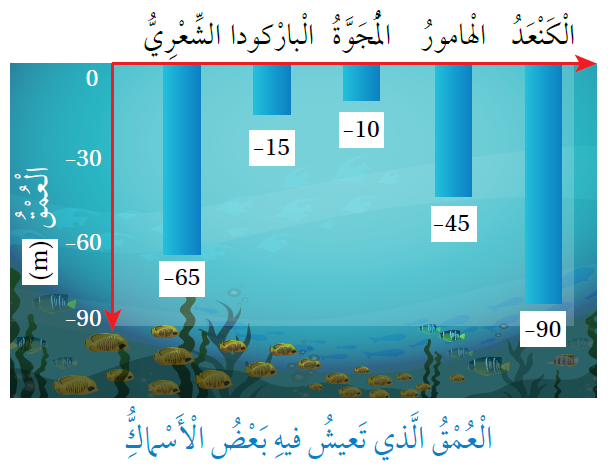
الجواب
الأعماق الّتي تعيشُ فيها هذه الأسماكُ هي:
مُعدّل العُمق () هُو مجموعُ الأعماق مقسومًا على عددها.
أي إنّ مُعدّل الأعماق الّتي تعيشُ فيها هذه الأسماكُ هُو: