تدريب صفحة
س ص ع مثلث قائم في ص ، فيه : ، جد ظا س ، ظا ع . 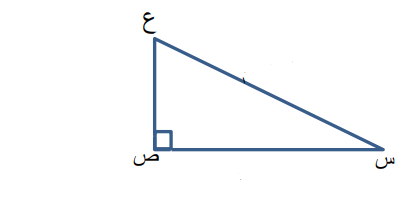
تدريب صفحة
في الشكل : و النقطة ج تقع على محور الصادات الموجب .
جد : 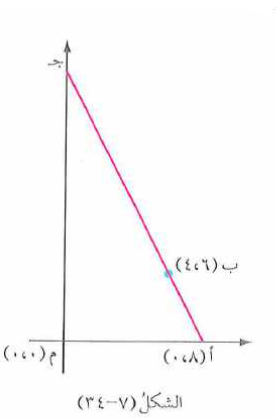
أنزل عمود من النقطة ب على محور السينات عند النقطة ن
احداثيات النقطة ن
تدريب صفحة
و قف أحمد على بعد من قاعدة بناية ، وكان قياس الزاوية المحصورة بين خط نظره المار بقمة البناية و الخط الأفقي ، إذا كان طول أحمد ،
كيف تساعد أحمد في حساب ارتفاع البناية . 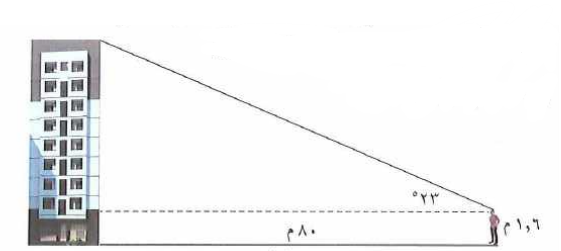
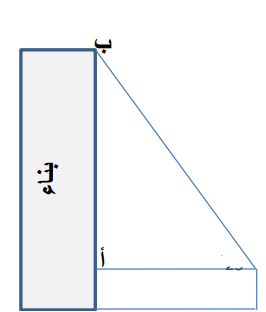
ارتفاع البناية = طول أحمد + طول الضلع أ ب
تمارين و مسائل صفحة
يمثل الشكل مثلثًا قائم الزاوية في ب ، فيه أج = ، ، جد كلاً مما يأتي :
أ) ب ج ب) ظا أ ج) ظا ج 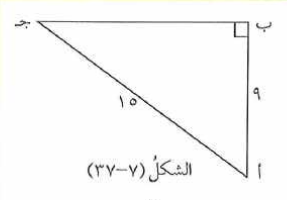
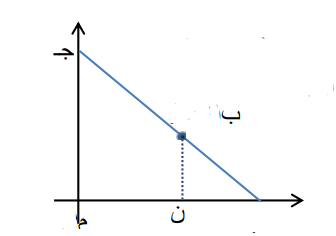
د م ن مثلث متطابق الضلعين فيه ، جد 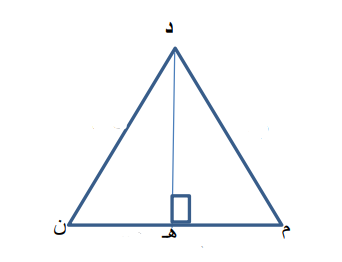
أ) ظا م ب ) ظا ن
قطعة أرض مستطيلة الشكل ظولها ، فأذا كان قطر القطعة يصنع زاوية مقدارها مع ضلعها الأصغر ، كما في الشكل ،
فما عرض قطعة الأرض ؟ 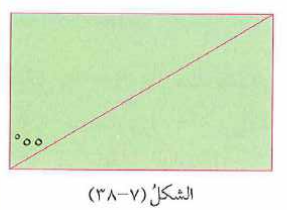
س ص ع مثلث قائم الزاوية في ص ، فيه : ، جد طول س ع .

استخدم الشكل في إيجاد
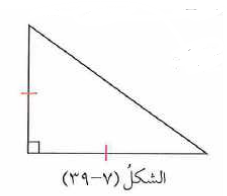 المثلث القائم متطابق الضلغين قياس الزاويتين الحادتين =
المثلث القائم متطابق الضلغين قياس الزاويتين الحادتين =
نفرض أن طول كل من الضلعين المتطابقين يساوي س
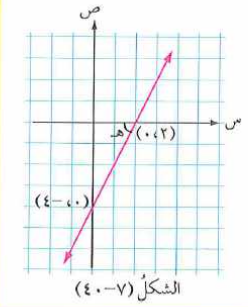
المستقيم ، يقطع محوري السينات و الصادات عند النقطتين على الترتيب ، و يشكل مع المحورين الإحداثيين مثلثًا
كما في الشكل ، تمثل الزاوية الحادة التي يصنعها المستقيم مع محور السينات . جد كلاً مما يأتي :
أ) جا هـ ب) جتا هـ ج ) ظا هـ