قابلية القسمة على 10, 5 ,3 ,2
الفكرة الرئيسية : اختبار قابلية القسمة على الأعداد 2 , 3 , 5 , 10 .
* يكون العدد قابلا للقسمة على عدد آخر إذا كان باقي القسمة صفرا وتوجد قواعد تساعدنا على معرفة ما إذا كان العدد يقبل القسمة على بعض الأعداد
أم لا دون إجراء عملية القسمة .
* قواعد قابلية القسمة :
1- يقبل العدد القسمة على 2 إذا كان العدد زوجي ( آحاده رقم زوجي). مثل : 1478 ، 456
2- يقبل العدد القسمة على 3 إذا كان مجموع أرقام منازله يقبل القسمة على 3. مثل : 25131 ، 95121
3- يقبل العدد القسمة على 5 إذا كان رقم آحاده 0 أو 5 . مثل : 7365 ، 2350
4- يقبل العدد القسمة على 10 إذا كان رقم آحاده 0 . مثل : 23470
* ملاحظة : تسمى الأعداد التي تقبل القسمة على 2 أعداد زوجية , كما تسمى الأعداد التي لا تقبل القسمة على 2 أعداد فردية .
مثال :
|
1- اختبر قابلية قسمة العدد 5316 على 2. الجواب :
منزلة الآحاد هي 6 وهو عدد زوجي لذا فإن العدد 5316 يقبل القسمة على 2.
|
2- اختبر قابلية قسمة العدد 4958 على 3 . الجواب :
بما أن مجموع أرقامه : 8+5+9+4 = 26 . والعدد 26 لا يقبل القسمة على 3 , لذا فإن العدد 4958 لا يقبل القسمة على 3
|
|
3- اختبر قابلية قسمة العدد 3974 على 5 . الجواب :
بما أن منزلة الآحاد في العدد 3974 ليس 0 أو 5 . لذا فإن العدد 3974 لا يقبل القسمة على 5 . |
4- اختبر قابلية قسمة العدد 9310 على 10 . الجواب :
منزلة الآحاد في العدد 9310 هي 0 . لذا فإن العدد 9310 يقبل القسمة على 10 . |
ويمكنني استعمال قابلية القسمة في تطبيقات الحياة اليومية ..
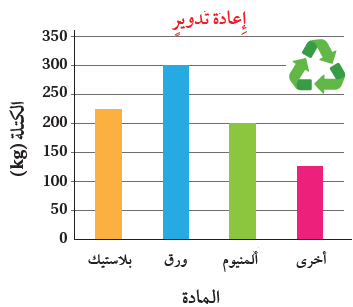
مثال : تسعى مدرسة لتشجيع طلبتها على جمع المواد التي يمكن إعادة تدويرها حفاظا على البيئة وقد جمع الطلبة كميات كما في التمثيل المجاور , هل يمكنني توزيع مادة البلاستك في عبوات سعة أو من دون أن يتبقى منها شيء ’ أفسر إجابتي .
|
الجواب : ألاحظ من التمثيل السابق أن كتلة العبوات البلاستيكية , ولتحديد أي العبوات يمكنني توزيع مادة (البلاستيك ) فيها , أختبر قابلية قسمة العدد 225 على كل من 5 و 10 .
أولا : أختبر قابلية قسمة العدد 225 على 5 . ألاحظ أن منزلة الآحاد في العدد 225 هي 5 . لذا فإن العدد 225 يقبل القسمة على 5 .
ثانيا : أختبر قابلية قسمة العدد 225 على 10 . ألاحظ أن منزلة الآحاد في العدد 255 هي 5 . لذا فإن العدد لا يقبل القسمة على 10 . |
|