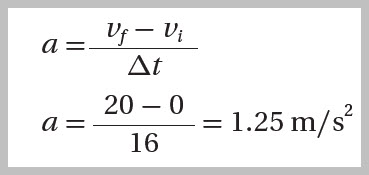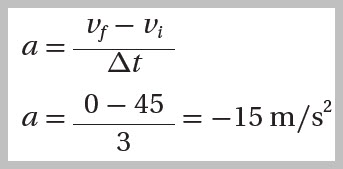مفهومُ القوّةِ Concept of Force
أنظرُ حولي فأرى أجسامًا ساكنةً وأخرى متحرّكةً، وأراقبُ الأجسامَ مدّةً منَ الزمنِ،
فأجدُ أنَّ الجسمَ الساكنَ قد يتحرّكُ، والجسمَ المتحرّكَ قد يتغيّرُ مقدارُ سرعتِه
أو اتجاهُ حركتِه أو كلاهما معًا؛ والسببُ في ذلكَ هو تأثيرُ القوى المختلفةِ في
الأجسامِ. فمثلاً، القوى المؤثّرةُ في الطائرةِ عندَ إقلاعِها تختلفُ عن القوى المؤثّرةِ
في الطائرةِ التي تقفُ على مدرجِ المطارِ. أتأمّلُ الشكلَ ( 1).

الشكل (1): تتغير الحالة الحركية للطائرة من السكون إلى الحركة بسبب
تغير القوى المؤثرة فيها.
تُعرَّفُ القوّةُ Force بأنَّها تأثيرٌ يؤدّي إلى تغييرٍ في حالةِ الجسمِ الحركيّةِ،
فمثلاً عندَما أدفعُ جسمًا أو أسحبُه فقد أحرّكُه إنْ كانِ ساكنًا، وقد أوقِفُه
إنْ كانَ متحرّكًا. وكذلك عندَما أرفعُ جسمًا ثمَّ أتركُه فإنَّ الأرضَ تؤثّرُ فيهِ بقوّةٍ.
تصنيفُ القوى Classification of Forces
درستُ في صفوفٍ سابقةٍ أنواعًا مختلفةً منَ القوى مثلُ قوّةِ الجاذبيّةِ، وقوّةِ
الشدِّ، وقوّةِ الاحتكاكِ، والقوّةِ الكهربائيّةِ. ويمكنُ تصنيفُ القوى جميعُها
ضمنَ فئتينِ، هما: قوى التلامسِ، وقوى التأثيرِ عنْ بُعْد.
قوى التلامسِ Contact Forces
قوًى تتطلبُ تلامسًا مباشرًا بينَ الأجسامِ، فمثلاً، عندَما يركلُ لاعبٌ كرةً بقدمِه،
فإنَّ القوّةَ التي يؤثّرُ بها اللاعبُ في الكرةِ هي قوّةُ تلامسٍ؛ لأنَّ التأثيرَ في الكرةِ
يتطلبُ تلامسًا مباشرًا بينَ القدمِ والكرةِ. ومنَ الأمثلةِ على قوى التلامسِ، القوةُ
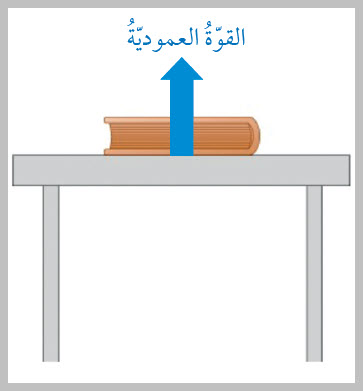
العموديّةُ؛ وهي قوّةٌ تنشأُ بينَ الجسمِ والسطحِ الذي يوضعُ عليهِ، وتكونُ دائمًا
عموديّةً على سطحِ التلامُسِ، ويبيّنُ الشكلُ (2) القوّةَ العموديّةَ المؤثّرةَ في كتابٍ
موضوعٍ على سطحِ طاولةٍ أفقيٍّ.
قوى التأثيرِ عن بُعْد Action-at-a-Distance Forces
قوًى تنشأُ بينَ الأجسامِ دونَ الحاجةِ إلى وجودِ تلامسٍ مباشرٍ بينَها، مثلُ قوّةِ
الجاذبيّةِ؛ فالجسمُ الموضوعُ على ارتفاعٍ ما عنْ سطحِ الأرضِ يتأثّرُ بقوّةِ الجاذبيّةِ
على الرغمِ منْ عدمِ وجودِ تلامسٍ بينَه وبينَ الأرضِ، وعندَ تركِه حرًّا يسقطُ نحوَ
الأرضِ بتأثيرِ هذهِ القوةِ. وكذلكَ تُعدُّ القوّةُ المغناطيسيّةُ والقوّةُ الكهربائيّةُ قوى
تأثيرٍ عنْ بُعْد. أتأمّلُ الشكلَ ( 3).

الشكل (3): يؤثّرُ البالونُ المشحونُ في قصاصاتِ الورقِ الموجودةِ على الأرضِ
بقوّةِ جذبٍ، على الرغمِ من عدمِ وجودِ تلامسٍ مباشرٍ بينَهما، فتنجذبُ نحوَهُ.
التأثيراتُ الناتجةُ عنِ القوى Effects of Forces
تؤثّرُ القوى في الأجسامِ بطرائقَ مختلفةٍ. ويمكنُ فهمُ الأثرِ الناتجِ عنِ القوى،
ووصفُ الحالةِ الحركيّةِ للأجسامِ بتطبيقِ قوانينِ نيوتن.
القانونُ الأولُ لِنيوتنَ في الحركةِ Newton’s First law of Motion
يبيّنُ الشكلُ ( 4/أ) قرصًا أملسَ موضوعًا على سطحٍ أفقيٍّ خشنٍ، يتأثّرُ القرصُ
بقوّتينِ؛ هما: القوّةُ العموديّةُ ( FN ) واتجاهُها إلى الأعلى، والوزنُ ( Fg ) واتجاهُه
إلى الأسفلِ.
ولمّا كانَ القرصُ يستقرُّ ساكنًا، فإنَّ محصّلةَ هاتينِ القوّتينِ تساوي صفرًا.
عندَما تدفعُ اليدُ القرصَ نحوَ اليمينِ، يكتسبُ القرصُ طاقةً حركيّةً، وبما أن
اليدَ تنفصلُ عنِ القرصِ مباشرةً بعدَ دفعِه في الاتجاهِ الأفقيِّ، فإن القرصَ
بالاتجاهِ الأفقيِّ يتأثرُ فقطْ بقوّةِ الاحتكاكِ أتأمّلُ الشكلَ (4/ب).
ونظرًا إلى أنَّ قوةَ الاحتكاكِ بعكسِ اتجاهِ الحركةِ، فإنَّها ستعملُ على إبطاءِ
سرعةِ القرصِ تدريجيًّا إلى أنْ يتوقّفَ.أما الشكلُ( 4/ج) فيوضّحُ القرصَ نفسه،
لكنّ الحركةَ على سطحٍ أملسَ. وفي هذهِ الحالةِ تكونُ محصّلةُ القوّةِ بالاتجاهِ
الأفقيِّ صفرًا، لذا يستمرُّ القرصُ بالحركةِ في خطٍّ مستقيمٍ وبسرعةٍ ثابتةٍ دونَ
توقّفٍ.
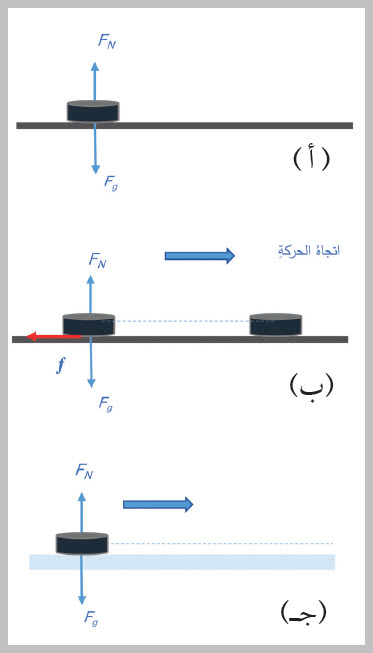
الشكل (4):
(أ) القرصُ ساكنٌ والقوّةُ المحصّلةُ تساوي صفرًا.
(ب) القرصُ يتحرّكُ بسرعةٍ متناقصةٍ، والقوّةُ المحصّلةُ لا تساوي صفرًا
وبعكسِ اتجاهِ الحركةِ.
(ج) القرصُ يتحرّكُ بسرعةٍ ثابتةٍ، والقوةُ المحصّلةُ تساوي صفرًا.
نستنتجُ ممّا سبقَ الأمرينِ الآتيينِ:
• القوّةُ المحصّلةُ المؤثّرةُ في الجسم الساكن ، وكذلك الجسم المتحرك
بسرعةٍ ثابتةٍ في خطٍّ مستقيمٍ، تساوي صفر.
• الجسمُ عاجزٌ عن تغييرِ حالتِه الحركيّةِ من تلقاءِ نفسِه؛ فالجسمُ الساكنُ
لا يمكنُ أنْ يتحرّكَ إلا إذا أثّرتْ فيهِ قوّةٌ محصّلةُ، والجسمُ المتحركُ بسرعةٍ ثابتةٍ
في خطٍّ مستقيمٍ لا يمكنُ أن يغيّرَ من مقدارِ سرعتِه أو اتجاهِها إلا إذا أثّرتْ فيهِ
قوةٌ محصّلةٌ.
ويُمكنُ تعميمُ النتيجةِ التي توصّلْنا إليها بصيغةٍ عبّرَ عنها العالمُ نيوتن بما يُعرفُ
بالقانونِ الأولِ لنيوتن Newton’s First law وينصُّ على أنَّ:
(( الجسمَ يحافظُ على حالتِه الحركيّةِ من حيثُ السكونُ، أو الحركةُ في خطٍّ مستقيمٍ
وبسرعةٍ ثابتةٍ، ما لم تؤثّرْ فيهِ قوّةٌ خارجيّةٌ محصّلةٌ تُغيّرُ حالتَه الحركيّةَ)).
السرعةُ الثابتةُ Constant Velocity
عندَما يتحركُ الجسمُ في خطٍّ مستقيمٍ بسرعةٍ ثابتةٍ؛ فإنَّه يقطعُ إزاحاتٍ متساويةً
في أزمنةٍ متساويةٍ، وتُوصفُ سرعتُه بأنَّها مُنتظَمةٌ.
ويبيّنُ الشكلُ (5/أ) مثالً على الحركةِ بسرعةٍ منتظمةٍ، فالجسمُ يتحركُ بخطٍّ مستقيمٍ
نحوَ اليمينِ باتجاهِ محورِ ( x+)، بسرعةٍ ثابتةٍ مقدارُها ، وهذا يعني أنَّ الجسمَ
يقطعُ إزاحةً مقدارُها في كلِّ ثانيةٍ من زمنِ الحركةِ.
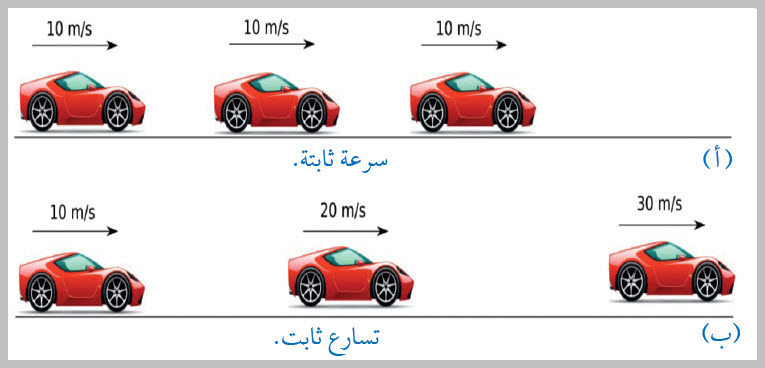
الشكل ( 5):
(أ) السيارةُ تتحركُ بسرعةٍ ثابتةٍ.
(ب) السيارةُ تتحركُ بتسارعٍ ثابتٍ.
أتأمّلُ الشكلَ، وأُحدّدُ في أيِّ الحالتين تكونُ القوّةُ المحصّلةُ المؤثّرةُ في السيارةِ صفرًا؟
وتُحسبُ السرعةُ الثابتةُ بقسمةِ الإزاحةِ المقطوعةِ ( Δx ) خلالَ مدّةٍ زمنيّة ( Δt) على
الزمنِ اللازمِ لحدوثِ تلكَ الإزاحةِ:
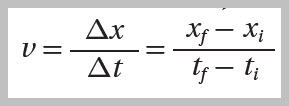
التسارعُ الثابتُ Constant Acceleration
لوصفِ حركةِ الأجسامِ عندَما تتحركُ بسرعةٍ متغيرةٍ، يستخدمُ العلماءُ مفهومَ
التسارُعِ. ويبيّنُ الشكلُ ( 5/ب) سيارةً تتحركُ بخطٍ مستقيمٍ، وعندَ رصدِ حركةِ
السيارةِ مدةً منَ الزمنِ، لوحظَ أنَّ السرعةَ تزدادُ بمقدارِ (10m/s) في كلِّ ثانيةٍ
من زمنِ الحركةِ، ما يعني أنَّ السرعةَ تزدادُ بانتظامٍ، لذا تُوصفُ السيارةُ بأنَّها
تتحركُ بتسارعٍ ثابتٍ يُرمز إليهِ بالرمزِ ( a)، ويُحسبُ بقسمةِ التغيّرِ في السرعةِ
على المدةِ الزمنيةِ التي حدث خلالَها هذا التغيّرُ:
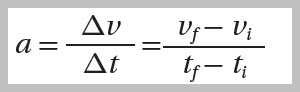
حيث: ( vf ) السرعة النهائية، ( vi ) السرعة الابتدائية.
يُقاسُ التسارعُ بوحدةِ ( m/s2 )، والسرعةُ والتسارعُ كميّاتٌ متّجهةٌ؛ أيْ إنَّ
لكلٍّ منها مقدارًا واتّجاهًا.
|
تمرين
أُحدّدُ لكلِّ جسمٍ ، هلْ يتحرّكُ بسرعةٍ ثابتةٍ أم متغيّرةٍ؟ موضِّحًا كيفَ توصّلْتُ إلى الإجابةِ. |
||||||||||||||||
|
يبدأُ قطارٌ حركتَه منَ السكونِ بتسارعٍ ثابتٍ في خطٍّ مستقيمٍ باتجاهِ محورِ ( x+)، فتزدادُ سرعتُه لتصبحَ (20m/s) بعدَ مرورِ (16s)، أحسُبُ تسارُعَ القطارِ. الحلُّ:
ألاحظُ أنَّ الحركةَ باتجاهِ محورِ ( x+) وإشارةَ التسارعِ موجبةٌ، أيْ إنَّ اتجاهِ التسارعِ باتجاهِ الحركةِ نفسِه، لذا فإنَّ القطارَ يتسارعُ. |
||||||||||||||||
|
سيارةُ سباقٍ تتحركُ بخطٍّ مستقيمٍ، تتناقصُ سرعتُها من ( ) إلى ( ) خلالَ ( ). أحسُب تسارُعَ السيارةِ. الحلُّ:
أُلاحظُ أنَّ الحركةَ باتجاهِ محورِ ( x+) وإشارةَ التسارعِ سالبةٌ، أيْ إنَّ اتجاهَ التسارعِ بعكسِ اتجاهِالحركةِ، فتناقصَتْ سرعةُ السيارةِ من ( ) إلى صفرٍ، لذا توصفُ السيارةُ بأنَّها تتباطأُ. |
||||||||||||||||
|
تمرين تقطعُ سيارةٌ ( ) خلالَ ( ). أحسُبُ سرعةَ السيارةِ بوحدةِ (). |
||||||||||||||||
|
القانونُ الثاني لنيوتن في الحركةِ Newton’s Second law of Motion تعلّمْتُ منَ القانونِ الأولِ لنيوتن أنَّ تغييرَ سرعةِ الجسمِ يتطلّبُ قوّةً محصّلةً، وعندَما تتغيرُ السرعةُ، فإنَّ الجسمَ يتحركُ بتسارعٍ. القانونُ الثاني لنيوتن يوضّحُ العلاقةَ بينَ التسارعِ والقوّةِ المحصّلةِ المسبِّبةِ لهُ. ستقتصرُ دراستُنا على تطبيقِ القانونِ الثاني لنيوتن على أجسامٍ تتحركُ بخطٍّ مستقيمٍ، ولا تتغيّرُ كتلتُها في أثناءِ الحركةِ (كتلةُ الجسمِ ثابتةٌ)، وبذلكَ يمكنُ صياغةُ القانونِ الثاني لنيوتن Newton’s Second law على النحوِ الآتي: «تسارعُ جسمٍ يتناسبُ طرديًّا معَ محصّلةِ القوّةِ المؤثِّرةِ فيهِ، وعكسيًّا معَ كتلتِه ». ونعبّرُ عنهُ رياضيًّا بالعلاقةِ الآتيةِ:
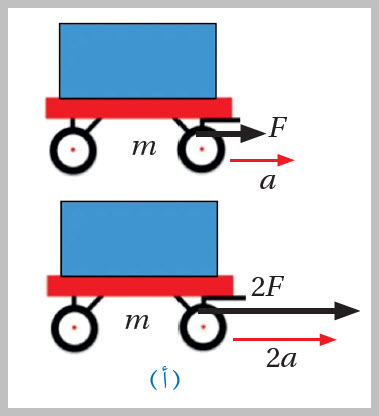
حيثُ: ( ΣF ) القوّةُ المحصّلةُ المؤثّرةُ في الجسمِ، وتُقاسُ بوحدةِ النيوتن (N).(m) كتلةُ الجسمِ، وتُقاسُ بوحدةِ (kg). (a) تسارعُ الجسمِ، ويُقاسُ بوحدةِ (m/s2)ففي الشكلِ (6/أ)، يمثّلُ الرمزُ ( F) القوّةَ المحصّلةَ المؤثّرةَ في العربةِ، وعندَما يتضاعفُ مقدارُ القوّةِ ليصبحَ ( 2F )، فإنَّ تسارُعَ العربةِ سوفَ يتضاعفُ. وبكتابةِ العلاقةِ بالصورةِ: ( )
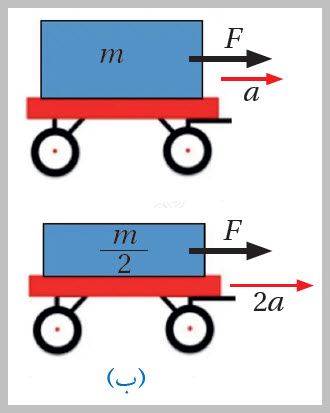
(أ)يتناسبُ التسارعُ طرديًّا معَ القوّةِ المحصّلةِ بثبوتِ الكتلةِ. يتّضح التسارعَ يتناسبُ عكسيًّا معَ الكتلةِ بثبوتِ القوّةِ المحصّلة. أتأمل الشكل (6/ب) الذي يوضّحُ أنَّ استبدالَ جسمٍ كتلتُهُ ( ) بالجسمِ الذي كتلتُه (m) يؤدّي إلى زيادةِ التسارعِ إلى الضعفِ، بثبوتِ القوّةِ المحصّلةِ.
(ب) يتناسبُ التسارعُ عكسيًّا معَ الكتلةِ بثبوتِ القوّةِ المحصّلةِ. مثال محلول أحسُبُ القوّةَ المحصّلةّ اللازمةَ كي يكتسبَ جسمٌ كتلتُه ( ) تسارُعًا ثابتًا مقدارُه ( ). الحلُّ:
|
|
|||||||||||||||
|
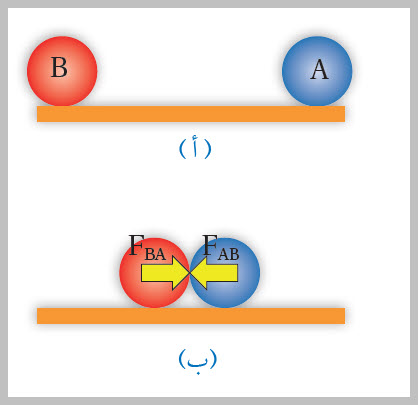
القانونُ الثالثُ لنيوتن Newton's Third law ((إذا تفاعلَ جسمانِ ( B ،A ) فإنَّ القوةَ التي يؤثّرُ بها الجسمُ (A) في الجسمِ ( B) تساوي في المقدارِ وتعاكسُ في الاتجاهِ القوّةَ التي يؤثّرُ بها الجسمُ ( B) في الجسمِ (A) . فمثلًا يبيّنُ الشكلُ (7/أ) كرتينِ (B ،A) تتحركانِ باتجاهينِ متعاكسينِ، لحظةَ تصادمِ الكرتينِ، تؤثّرُ الكرةُ (A) في الكرةِ (B) بقوةِ دفعٍ (FAB) ،وكذلكَ تؤثّرُ الكرة (B) في الكرةِ (A) بقوةِ دفعٍ مساويةٍ في المقدارِ ومعاكسةٍ في الاتجاهِ (FBA). تُسمَّى إحدى القوّتينِ الفعلَ، وتُسمَّى القوةُ الأخرى ردَّ الفعلِ، وهما قوّتانِ متساويتانِ في المقدارِ، ومتعاكستانِ في الاتجاهِ (FAB = -FBA)، ومن النوعِ نفسِه، تنشآن في اللحظةِ نفسِها، وتؤثّرانِ في جسمينِ مختلفينِ، ويُسمّيانِ زوجًا؛ الفعلَ وردَّ الفعلِ. يُقدّمُ لنا قانونُ نيوتن الثالثُ تفسيرًا لمشاهداتٍ يوميّةٍ، مثلُ المشي.
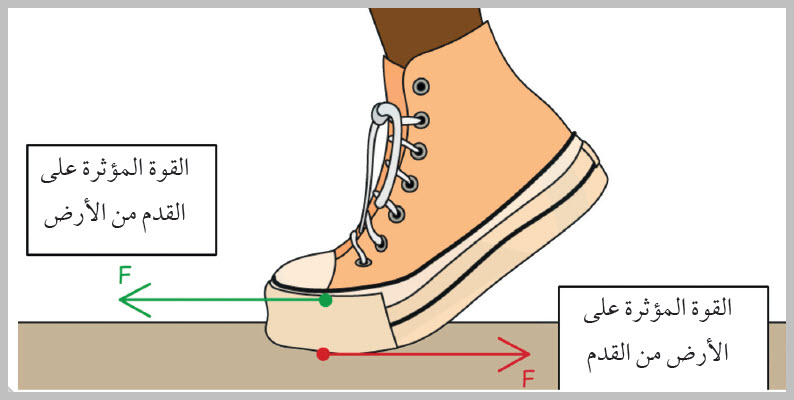
الشكل ( 7): (أ) كرتانِ تتحرّكانِ باتجاهينِ متعاكسينِ. (ب) لحظةَ التصادمِ تؤثّرُ كلُّ كرةٍ في الأخرى بقوّةِ دفعٍ، وتكونُ القوّتانِ متساويتينِ ومتعاكستينِ. ويبيّنُ الشكلُ ( 8) زوجَ القوى المؤثّرُ في كلٍّ منِ الأرضِ والقدمِ عندَ المشي. فعندَما تلامسُ القدمُ الأرضَ ينشأُ زوجٌ منَ القوى المتبادَلةِ بينِ الأرضِ والقدمِ؛ فتؤثّرُ القدمُ في الأرضِ بقوّةٍ إلى الخلفِ، وبالمقابلِ تؤثّرُ الأرضُ في القدمِ بقوّةٍ مساويةٍ في المقدارِ ومعاكسةٍ في الاتجاهِ فتدفعُها إلى الأمامِ.
الشكل ( 8): في أثناءِ المشي، تدفعُ القدمُ الأرضَ إلى الخلفِ فتدفعُ الأرضُ القدمَ إلى الأمام. |
|
|||||||||||||||
 مثال محلول
مثال محلول