رياضيات7 فصل أول

مفهوم أساسي:

 يمكنُني التعبيرُ عنِ الضربِ المتكرِّرِ للعددِ في نفسِهِ باستخدامِ الأسسِ، وعندئذٍ يُسمّى عددُ مرّاتِ تكرارِ الضربِ الأُسَّ (Exponent) ، أمّا العددُ نفسُهُ فيُسمّى الأساسَ (Base) ويُسمّى كلٌّ منَ الأساسِ والأُسِّ معًا القوَّةَ (Power)

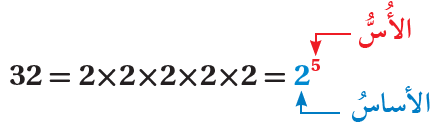
تُسمّى الصيغةُ التي يُكْتَبُ فيها الضربُ المتكرِّرُ باستخدامِ الأسسِ الصيغَةَ الأُسِّيَّةَ (Exponent form) مثل 3⁷

أمّا الصيغَةُ التي يُكْتَبُ فيها الضربُ المتكرّرُ منْ دونِ استخدامِ الأسسِ فتُسمّى الصيغةَ القياسيّةَ (Standard form) مثل 3×3×3×3×3×3×3

مثال 1: أكتبُ كلًّ ممّا يأتي بالصيغةِ الأُسِّيَّةِ:

1)5 ×5 × 3 × 3 × 3 × 3

الخاصية التجميعية        $=\left(3\times 3\times 3\times 3\right)\times \left(5\times 5\right)$

تعريفُ الأسسِ                                          $=3^4\times 5^2$                        

2)  a × a × c × a × c × c × a × a

الخاصية التبديلية             $=\mathrm{a}\times \mathrm{a}\times \mathrm{a}\times \mathrm{a}\times \mathrm{a}\times \mathrm{c}\times \mathrm{c}\times \mathrm{c}$            

الخاصية التجميع             $=\left(\mathrm{a}\times \mathrm{a}\times \mathrm{a}\times \mathrm{a}\times \mathrm{a}\right)\times \left(\mathrm{c}\times \mathrm{c}\times \mathrm{c}\right)$             

تعريفُ الأسسِ                                                        $= {\mathrm{a}}^5\times {\mathrm{c}}^3$

 

أستعملُ قواعدَ ضربِ القوى وقسمتِها الآتية لأبسِّطَ العباراتِ الأُسِّيةِ:

التعبيرُ اللفظيُّ	الرموزُ	السببُ
ضربُ القوى: لضربِ قوَّتينِ لهُما الأساسُ نفسُهُ، أجمعُ أُسَّيْهِما	${\mathbf{a}}^{\mathbf{m}}\mathbf{\times }\mathbf{ }{\mathbf{a}}^{\mathbf{n}}\mathbf{=}{\mathbf{a}}^{\mathbf{m}\mathbf{+}\mathbf{n}}$	$$\begin{gathered} {\mathbf{a}}^{\mathbf{3}}\mathbf{\times }{\mathbf{a}}^{\mathbf{5}}\mathbf{=}\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{)}\mathbf{\times }\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathbf{a}}^{\mathbf{8}} \end{gathered}$$
قسمةُ القوى: لقسمةِ قُوَّتينِ لهُما الأساسُ نفسُهُ، أطرحُ أُسَّ المقامِ منْ أسِّ البسطِ	$\frac{{\mathbf{a}}^{\mathbf{m}}}{{\mathbf{a}}^{\mathbf{n}}}\mathbf{=}{\mathbf{a}}^{\mathbf{m}\mathbf{-}\mathbf{n}}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{a}\mathbf{\ne }\mathbf{0}$	$$\begin{gathered} \frac{{\mathbf{a}}^{\mathbf{5}}}{{\mathbf{a}}^{\mathbf{2}}} \mathbf{=}\frac{\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\cancel{\mathbf{a}}\mathbf{\times }\cancel{\mathbf{a}}\mathbf{\times }\cancel{\mathbf{a}}}{\cancel{\mathbf{a}}\mathbf{\times }\cancel{\mathbf{a}}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }{\mathbf{a}}^{\mathbf{3}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{a}\mathbf{\ne }\mathbf{0} \end{gathered}$$
قوَّةُ القوَّةِ: لإيجادِ قوَّةِ القوَّةِ، أضربُ الأسسَ	${\mathbf{(}\mathbf{ }{\mathbf{a}}^{\mathbf{m}}\mathbf{)}}^{\mathbf{ }\mathbf{n}}\mathbf{=}{\mathbf{a}}^{\mathbf{n}\mathbf{\times }\mathbf{m}}$	$$\begin{gathered} {\mathbf{\left(}{\mathbf{a}}^{\mathbf{3}}\mathbf{\right)}}^{\mathbf{2}} \mathbf{=}{\mathbf{a}}^{\mathbf{3}}\mathbf{\times }{\mathbf{a}}^{\mathbf{3}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{)}\mathbf{\times }\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathbf{a}}^{\mathbf{6}} \end{gathered}$$
قوَّةُ حاصلِ الضربِ: لإيجادِ قوَّةِ حاصلِ الضربِ، أجدُ قوَّةَ كلِّ عددٍ، ثمَّ أضربُ	${\mathbf{\left(}\mathbf{ab}\mathbf{\right)}}^{\mathbf{n}}\mathbf{ }\mathbf{=}{\mathbf{a}}^{\mathbf{n}}\mathbf{ }{\mathbf{b}}^{\mathbf{n}}\mathbf{ }$	$$\begin{gathered} {\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{b}\mathbf{)}}^{\mathbf{3}} \mathbf{=}\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{b}\mathbf{)}\mathbf{\times }\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{b}\mathbf{)}\mathbf{\times }\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{b}\mathbf{)}\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{(}\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{\times }\mathbf{a}\mathbf{)}\mathbf{\times }\mathbf{(}\mathbf{b}\mathbf{\times }\mathbf{b}\mathbf{\times }\mathbf{b}\mathbf{)} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}{\mathbf{a}}^{\mathbf{3}}\mathbf{\times }{\mathbf{b}}^{\mathbf{3}} \end{gathered}$$
قوَّةُ ناتجِ القسمةِ: لإيجادِ قوَّةِ ناتجِ القسمةِ، أجدُ كلًّ منْ قوَّةِ البسطِ والمقامِ، ثمَّ أقسمُ.	${\mathbf{\left(}\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\right)}}^{\mathbf{n}}\mathbf{=}\frac{{\mathbf{a}}^{\mathbf{n}}}{{\mathbf{b}}^{\mathbf{n}}}$	$$\begin{gathered} {\mathbf{\left(}\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\right)}}^{\mathbf{2}} \mathbf{=}\frac{\mathbf{a}}{\mathbf{b}}\mathbf{\times }\frac{\mathbf{a}}{\mathbf{b}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\frac{\mathbf{a}\mathbf{\times }\mathbf{a}}{\mathbf{b}\mathbf{\times }\mathbf{b}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\frac{{\mathbf{a}}^{\mathbf{2}}}{{\mathbf{b}}^{\mathbf{2}}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{b}\mathbf{\ne }\mathbf{0}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ } \end{gathered}$$

مثال 2 :أستخدمُ قوانينَ الأسسِ لإيجادِ قيمةِ كلٍّ ممّا يأتي:

1) ${\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{)}}^{\mathbf{3}}\mathbf{\times }{\mathbf{(}\mathbf{-}\mathbf{2}\mathbf{)}}^{\mathbf{4}}$

قاعدة ضرب القوى          ${(-2)}^3\times {(-2)}^4={(-2)}^{3+4}$                     

أجمع الأسس                  $={(-2)}^7$                                         

تعريف الأسس               $=-128$                                           

2)$\frac{{\mathbf{3}}^{\mathbf{8}}}{{\mathbf{3}}^{\mathbf{7}}}$

قاعدةُ قسمةِ القُوى                      $\frac{3^8}{3^7}=3^{8-7}$                                            

أطرحُ الأسسَ                                $=3$    

3) ${\mathbf{(}{\mathbf{2}}^{\mathbf{3}}\mathbf{\times }\mathbf{5}\mathbf{)}}^{\mathbf{2}}$

قاعدةُ قوَّةِ حاصلِ الضربِ                ${\left(2^3\times 5\right)}^2=2^6\times 5^2$

تعريفُ الأسسِ                                $=64\times 25$ 

أضربُ                                               $=1600$                                             

هلْ يمكنُ أنْ يكونَ الأسُّ سالبًا؟ بِتَتَبُّعِ النمطِ في الجدولِ الآتي، ألاحظُ أنَّ الأسسَ الصحيحةَ السالبةَ للعددِ 10 تمثِّلُ قسمةً . متكرِّرةً للعددِ 10 على نفسِهِ، وألاحظُ أيضًا أنَّ قيمةَ 10⁰ هي 1

الصيغةُ الأُسِّيَّةُ	103	102	101	100	10-1	10-2	10-3
القيمةُ العدَدِيَّةُ	1000	100	10	1	$\frac{1}{10}$	$\frac{1}{100}$	$\frac{1}{1000}$

إنَّ الاستنتاجَيْنِ اللَّذَيْنِ توصَّلْتُ إليهِما عنِ الأسسِ الصحيحةِ السالبةِ والأسِّ الصِّفْرِيِّ صحيحانِ لأيِّ عددٍ (ما عدا الصفرِ) ويمكنُني التحقُّقُ منْ ذلكَ بإنشاءِ جداولَ مشابهةٍ لأعدادٍ أخرى غيرِ العددِ 10 . يمكنُني تعميمُ هذَيْنِ الاستنتاجَيْنِ على النحوِ الآتي:

التعبيرُ اللفظيُّ	الرموزُ	السببُ
الأسُّ الصِّفْرِيُّ: أيُّ عددٍ غيرِ الصفرِ مرفوعًا للأسِّ صفرٍ يساوي 1	${\mathbf{a}}^{\mathbf{0}}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{1}$	$\mathbf{1}\mathbf{=}\frac{{\mathbf{a}}^{\mathbf{2}}}{{\mathbf{a}}^{\mathbf{2}}}\mathbf{=}{\mathbf{a}}^{\mathbf{0}}$
الأسسُ السالبةُ: القوَّةُ ذاتُ الأساسِ غيرِ الصفريِّ والأُسُّ السالبُ هِيَ مقلوبُ القوَّةِ ذاتِ الأساسِ غيرِ الصفريِّ والأُسِّ الموجبِ، والعكسُ صحيحٌ.	${\mathbf{a}}^{\mathbf{-}\mathbf{n}}\mathbf{=}\frac{\mathbf{1}}{{\mathbf{a}}^{\mathbf{n}}}$ $\mathbf{ }{\mathbf{a}}^{\mathbf{n}}\mathbf{=}\frac{\mathbf{1}}{{\mathbf{a}}^{\mathbf{-}\mathbf{n}}}$	$$\begin{gathered} {\mathbf{a}}^{\mathbf{-}\mathbf{3}}\mathbf{ }\mathbf{=}{\mathbf{a}}^{\mathbf{-}\mathbf{1}}\mathbf{\times }{\mathbf{a}}^{\mathbf{-}\mathbf{1}}\mathbf{\times }{\mathbf{a}}^{\mathbf{-}\mathbf{1}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\frac{\mathbf{1}}{\mathbf{a}}\mathbf{\times }\frac{\mathbf{1}}{\mathbf{a}}\mathbf{\times }\frac{\mathbf{1}}{\mathbf{a}} \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{=}\frac{\mathbf{1}}{{\mathbf{a}}^{\mathbf{3}}} \end{gathered}$$

 مثال 3 : أستخدمُ قوانينَ الأسسِ لإيجادِ قيمةِ كلٍّ ممّا يأتي:

1) 5^-2

قاعدةُ الأسسِ السالبةِ                            ^{$5^{-2}=\frac{1}{5^2}$} 

تعريفُ الأسسِ                                        ^{$=\frac{1}{25}$} 

2) $\frac{{\mathbf{6}}^{\mathbf{5}}\mathbf{\times }{\mathbf{10}}^{\mathbf{3}}}{{\mathbf{6}}^{\mathbf{2}}\mathbf{\times }{\mathbf{10}}^{\mathbf{6}}}$

قاعدةُ الأسسِ السالبةِ                    $\frac{6^5\times {10}^3}{6^2\times {10}^6}=\frac{6^5\times 6^{-2}}{{10}^6\times {10}^{-3}}$ 

قاعدةُ قوَّةِ ناتجِ القسمةِ                              $=\frac{6^3}{{10}^3}$

تعريفُ الأسسِ                               $$\begin{gathered} =\frac{216}{1000} \\ =0.216 \end{gathered}$$