رسم الزاوية في الوضع القياسي
تعلمت سابقاً أن الزاوية المرسومة في الوضع القياسي في المستوى الإحداثي هي زاوية يقع رأسها عند نقطة الأصل (0,0) ، وضلع ابتدائها منطبق على المحور x الموجب .
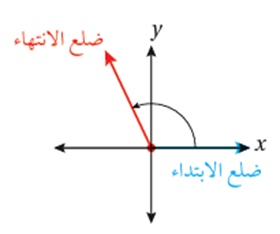
تعلمت أيضاً أن قياس الزاوية يصف مقدار الدوران واتجاهه اللازمين للانتقال من ضلع الابتداء إلى ضلع الانتهاء ، وأن قياس الزاوية يكون موجباً اذا كان دوران ضلع الانتهاء عكس اتجاه حركة عقارب الساعة ، وسالباً اذا كان دوران ضلع الانتهاء مع اتجاه حركة عقارب الساعة .
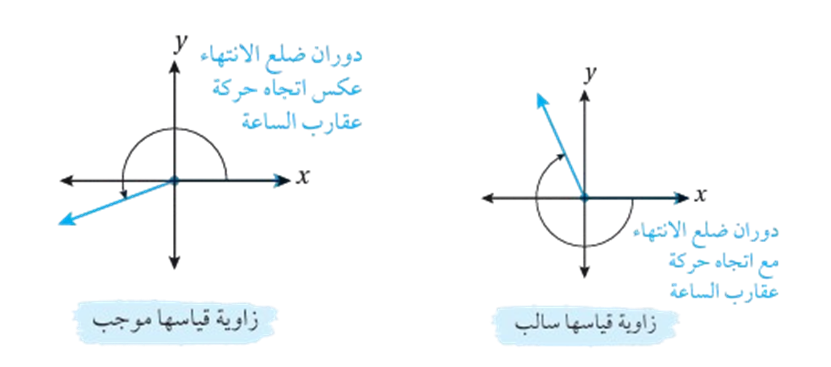
مثال: أرسم في الوضع القياسي الزاوية التي عُلم قياسها في كل مما يأتي :
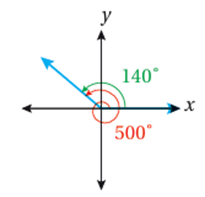
1) 500°
الزاوية 500° تزيد على الزاوية 360° بمقدار 140° ، فإن ضلع الانتهاء أكمل دورة كاملة عكس اتجاه دوران عقارب الساعة ، ثم دار أيضاً 140° عكس اتجاه دوران عقارب الساعة .
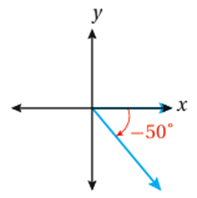
2)
الزاوية زاوية سالبة ، فأننا نرسم ضلع الانتهاء بالدوران 50° في اتجاه دوران عقارب الساعة ، بدءاً بالجزء الموجب من x
الراديان:
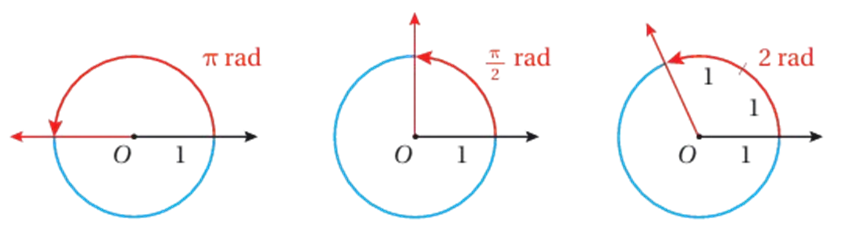
تعلمت سابقاً أنه يمكن قياس الزوايا بالدرجات ، ويمكن أيضاً قياسها بوحدة تعتمد على طول قوس الدائرة ، وتسمى الراديان . فقياس الزاوية المرسومة في الوضع القياسي ، التي يحدد ضلع انتهائها قوساً من الدائرة ، طوله مساوٍ لنصف قطر الدائرة ، هو 1 راديان .
وبما أن محيط الدائرة يساوي ، فإن قياس زاوية الدورة الكاملة هو راديان ( عدد مرات تكرار r في ) . وبذلك فإن القياس بالدرجات والقياس بالراديان مرتبطان بالمعادلة الآتية:
وهذه يعني أن قياس الزاوية المستقيمة ، وأن قياس الزاوية القائمة هو ، وأن قياس الزاوية التي يقابلها قوس طوله وحدتان هو .
وبما أن ، اذن ، ويمكن من خلال هاتين العلاقتين تحويل قياس أي زاوية من الدرجات إلى الراديان والعكس على النحو الآتي:

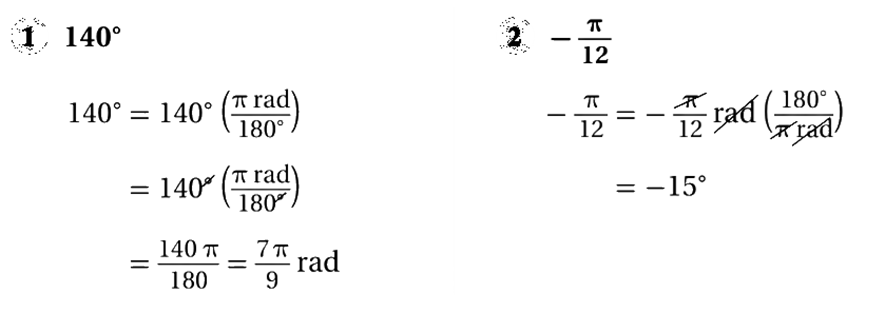
• مثال: حول قياس الزاوية المكتوبة بالدرجات إلى الراديان ، وقياس الزاوية المكتوبة بالراديان إلى الدرجات في كل مما يأتي :
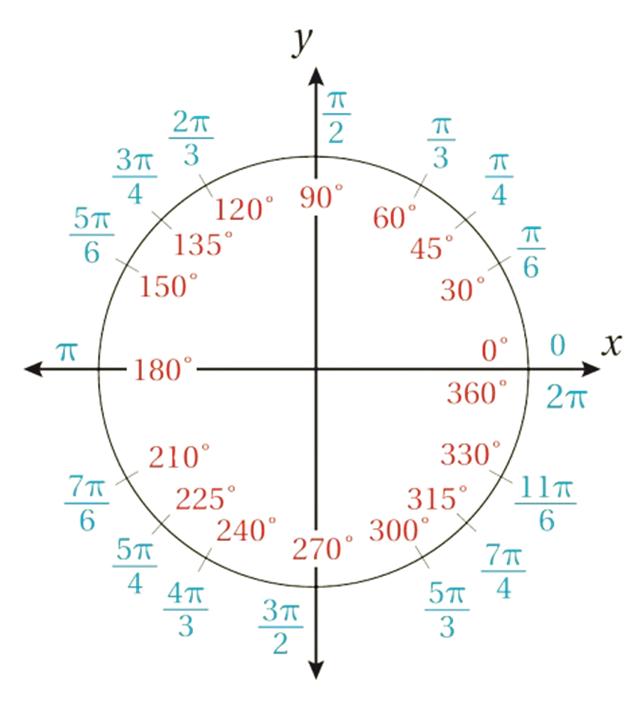
قياس الزوايا الخاصة بالدرجات والراديان:
يبين الشكل المجاور القياسات المتكافئة بالدرجات والراديان للزوايا الخاصة من 0° إلى360° ( من 0 rad إلى 2π rad ) .
• الزوايا المُشتركة:
يُمكِن إيجاد زاوية مُشتركة في ضلع الانتهاء مع زاوية أخرى عن طريق جمع أو طرح أحد مضاعفات الزاوية °360 أو 2T
بالدرجات
إذا كانت تُمثِّل القياس بالدرجات لزاوية ما، فإنَّ جميع الزوايا ذات القياس هي زوايا مشتركة مع ، حيث n عدد صحيح.
بالراديان
إذا كانت تُمثِّل القساس بالراديان لزاوية ما، فإنَّ جميع الزوايا ذات القياس هي زوايا مُشتركة مع ، حيث n عدد صحيح.
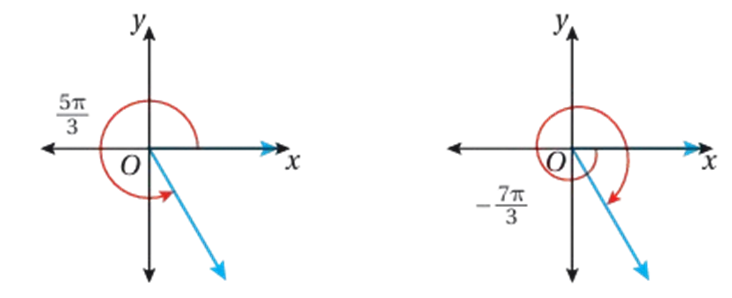
• مثال: جد زاويتين إحداهما قياسها موجب ، والأخرى قياسها سالب ، وكلتاهما مُشتركة في ضلع الانتهاء مع كل زاوية معطاة مما يأتي ، ثم أرسمها:
1)
أولاً بتعويض n=1 لإيجاد زاوية مشتركة قياسها موجب
ثانياً بتعويض n=-1 لإيجاد زاوية مشتركة قياسها سالب
بالرسم:
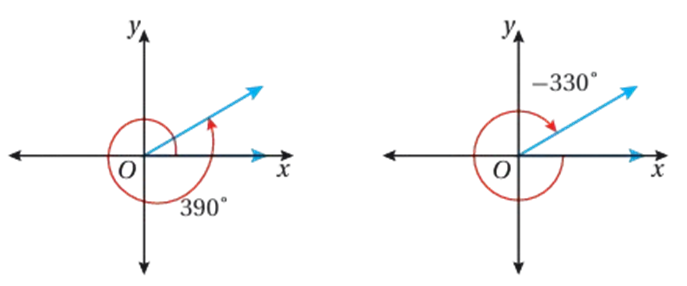
2)
أولاً: بتعويض n=1 لإيجاد زاوية مشتركة قياسها موجب
ثانياً: بتعويض n=-1 لإيجاد زاوية مشتركة قياسها سالب
بالرسم:
تطبيقات : طول القوس ومساحة القطاع
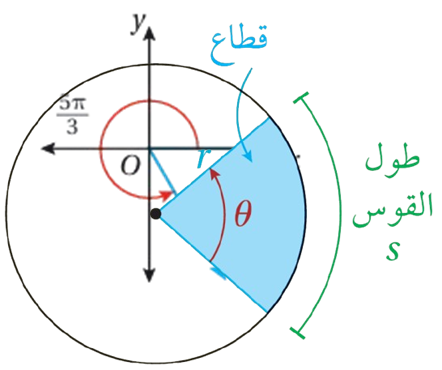
تعلمت سابقاً أن القوس جزء من الدائرة مُحدد بنقطتين عليها ، وأن القطاع هو الجزء المحصور بين قوس منها ونصفي القطرين اللذين يمران بطرفي القوس.
وسأتعلم الآن إيجاد طول القوس ومساحة القطاع عندما يكون قياس الزاوية المركزية بالراديان.
طول القوس:
مساحة القطاع:
حيث :
s : طول القوس r : نصف القطر
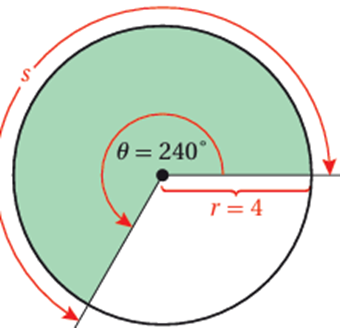
مثال: يبين الشكل المجاور قطاعاً دائرياً زاويته المركزية 240° في دائرة طول نصف قطرها 4cm . جد طول القوس ومساحة القطاع ، وأقرب إجابتي إلى أقرب جزء من عشرة .
الحل:
لإيجاد طول قوس القطاع الدائري باستعمال الصيغة : s=rθ ، نحول قياس زاوية القطاع من الدرجات الى الراديان .
الخطوة1: أحول قياس الزاوية المركزية من الدرجات إلى الراديان
الخطوة2: أجد طول القوس
الخطوة3: أجد مساحة القطاع
تطبيقات الحركة الدائرية:
يمكن وصف حركة نقطة تتحرك على محيط الدائرة كما في الشكل المجاور باستعمال السرعة الخطية التي تمثل المعدل الذي تتغير فيه المسافة المقطوعة . فالسرعة الخطية هي المسافة المقطوعة مقسومة على المدة الزمنية المنقضية .
ويمكن وصف حركة النقطة باستعمال السرعة الزاوية وهي التي تمثل المعدل الذي يتغير فيه قياس الزاوية المركزية . فالسرعة المركزية هي قيمة التغير في قياس الزاوية بالراديان مقسومة على الزمن المنقضي .
ويمكننا إيجاد السرعة الخطية من خلال العلاقة:
حيث : s طول القوس الذي تقطعه النقطة في مدة زمنية مقدارها t و v السرعة الخطية
ويمكننا ايجاد السرعة الزاوية من خلال العلاقة :
حيث ω : السرعة الزاوية
معلومة : الحرف اليوناني ω يقرأ اوميغا ويستعمل للدلالة على السرعة الزاوية .
مثال: يدور طفل حجراً مربوطاً بطرف حبل طول 3ft بمعدل 15 دورة في 10 ثوانٍ . جد السرعة الزاوية والسرعة الخطية للحجر
أولاً: نجد السرعة الزاوية
ثانياً: نجد السرعة الخطية .
بتعويض: