كتابة المتباينات وتمثيلها
تعريف المتباينة: جملة رياضية تقارن بين مقدارين وتشمل أحد الرموز
≤ ، ≥ ، < ، >
الجدول الآتي يوضح معنى الرموز :
رموز المتباينات
|
الرمز |
≤ |
≥ |
< |
> |
|
|
|
|
يتكون هذا الدرس من ثلاثة أفكار:
الفكرة الأولى: ترجمة عبارة لفظية الى متباينة.
مثال ( 1 ) : عدد أصغر من 12 ، المتغير هو عدد ونرمز له مثلا x
فتكون المتباينة : 12 > x
(ملاحظة : يمكن استبدال عبارة أصغر من بعبارة يقل عن أو أقل من)
مثال ( 2 ) : عدد أكبر من 100
لنفرض ان المتغير هو a
المتباينة: 100 < a
( ملاحظة : يمكن استبدال عبارة أكبر من بعبارة أكثر من أو يزيد على )
مثال ( 3 ) : طولي أقل من أو يساوي m 160
لنفرض أن المتغير هو L
المتباينة: 160 ≥ L
( ملاحظة: يمكن استبدال عبارة أقل أو يساوي بعبارة على الأكثر أو لا يزيد على )
مثال ( 4 ) : عدد المعلمين لا يقل على 15
لنفرض أن المتغيرهو n
المتباينة: 15 ≤ n
( ملاحظة: يمكن استبدال عبارة لا يقل بعبارة أكثر من أو يساوي ، على الأقل )
مثال ( 5 ) : عدد مطروح منه 5 أصغر من 19
لنفرض أن المتغير هو h
نلاحظ أن المتغير h تم طرح 5 منه وبالتالي
تكون المتباينة: 19 > h-5
مثال ( 6 ) : يلتحق الطفل في المدرسة عن عمر لا يقل عن 6 سنوات
( ملاحظة : نريد أن نعبر عن العبارة السابقة بمتباينة )
الكلمات: عمر الطفل لا يقل عن 6 سنوات
لنفرض أن المتغير x يمثل عمر الطفل
المتباينة: 6 ≤ x
...............................................................................................................................................................................................
الفكرة الثانية : حل المتباينة .
حل المتباينة: هو أي عدد يجعل المتباينة صحيحة .
( ملاحظة: يمكن أن يكون للمتباينة أكثر من حل ).
للتحقق ما إذا كانت قيمةً معطاة تمثل حل للمتباينة أم لا، نعوض هذه القيمة في المتباينة فإذا كانت:
1) إذا كانت المتباينة صحيحة فإن هذه القيمة تمثل حلاً للمتباينة.
2) وإذا كانت المتباينة غير صحيحة فإن هذه القيمة لا تمثل حلاً للمتباينة.
................................................................................................................................................................................................................................................................................
(a 4x – 3 > 6 , x = 5
نعوض القيمة المعطاة x = 5 في المتباينة
6 <؟ 3 – ( 5 ) 4
6 <؟ 3 – 20
6 < 17
النتيجة صحيحة..
إذا x=5 أحد حلول المتباينة.
...................................................................................................................................................................................................................................................................................
b) 15 – y < 3 , y = -5
نعوض: 3 >؟ ( 5- ) – 15
3 >؟ 5 + 15
3 > 20
النتيجة خاطئة..
وبالتالي 5-y = لا يمثل أحد حلول المتباينة.
....................................................................................................................................................................................................................................................................................
الفكرة الثالثة: تمثيل المتباينة على خط الأعداد.
مثال ( 8 ) : أمثل كل متباينة على خط الأعداد
1)
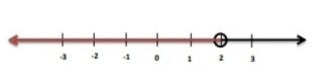
الدائرة المفتوحة عند 2 تعني أن 2 ليست أحد حلول المتباينة لأن الرمز ()
(ملاحظة : اللون الأحمر يمثل حل المتباينة )
....................................................................................................................................................................................................................................................................................
2) x 2
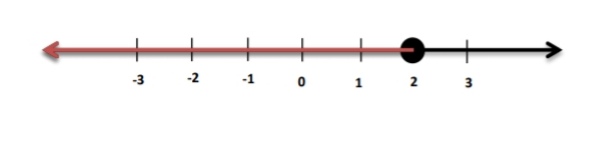
الدائرة المغلقة عند 2 تعني أن 2 أحد حلول المتباينة
.....................................................................................................................................................................................................................................................................................
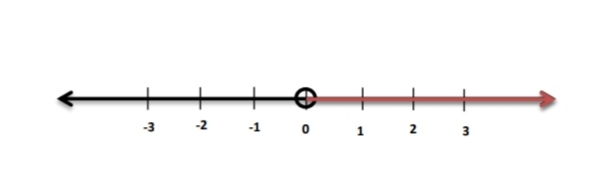
3) a 0
....................................................................................................................................................................................................................................................................................
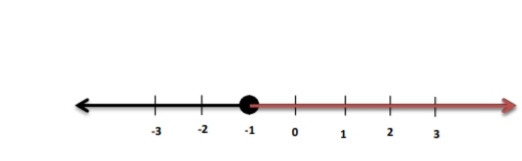
4) L -1
....................................................................................................................................................................................................................................................................................