فكرةُ الدّرس: أحسُبُ مساحات أشكالٍ مُركّبةٍ ومُحيطاتها.
المُصطلحاتُ: شكلٌ مُركّبٌ.
|
الشّكلُ المُركّبُ شكل هندسيناتجٌ عن تركيب شكلين هندسيّين أو أكثر.
مُحيطُ شكلٍ مُركّبٍ ناتجٍ من قصّ مُربّعٍ أو مُستطيلٍ من إحدى زواياهُ يُساوي مُحيط المُربّع أو المُستطيل قبل القصّ.
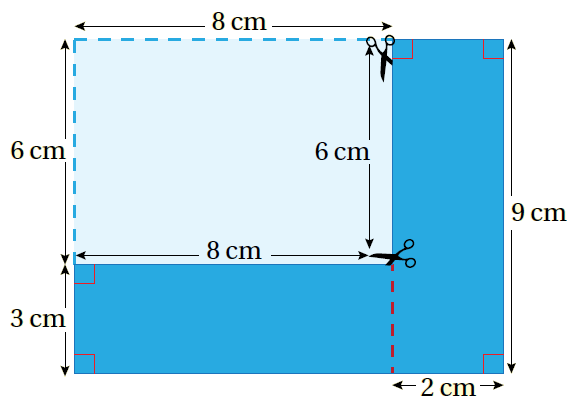
أُلاحظُ في الشّكل المُجاور أنّ مُحيط الشّكل النّاتج بعد القصّ يُساوي مُحيط المُستطيل الكبير؛ فكلا المُحيطين يُساوي 38cm |
 |
|
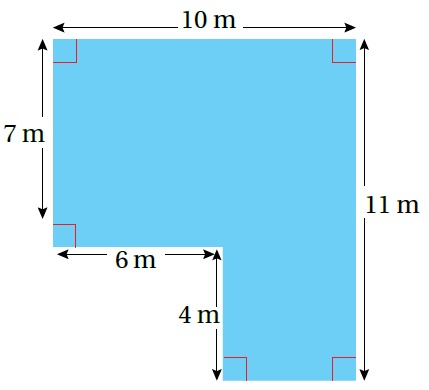
مثال أحسُبُ مُحيط الشّكل المُجاور الجواب الشّكلُ المُجاورُ ناتجٌ عن قصّ مُستطيلٍ صغيرٍ طولُهُ 6m وعرضُهُ 4m من أحد أركان مُستطيلٍ كبيرٍ. إذن: مُحيطُهُ يُساوي مُحيط المُستطيل الكبير. |
 |
|
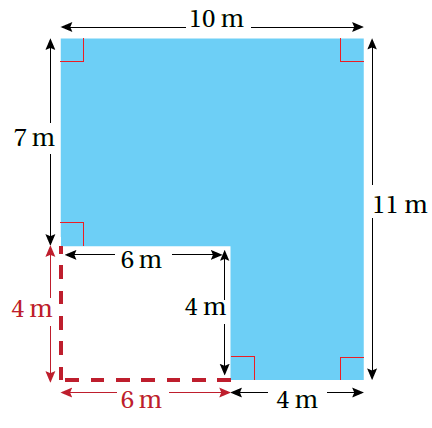
أُكملُ الشّكل، فينتُجُ مُستطيلٌ طولُهُ 11m وعرضُهُ 10m
إذن؛ محيط الشكل يُساوي: |
 |
لحساب مساحة شكلٍ مُركّبٍ يُمكنُني أيضًا أن أقسمهُ إلى مُستطيلاتٍ ومُربّعاتٍ، ثُم أحسُب مساحات هذه الأشكال وأجمعها.
|
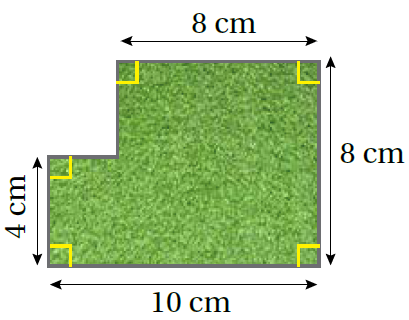
مثال أحسُبُ مساحة مُخطّط الحديقة في الشّكل المُجاور. الجواب |
 |
||||||||||
|
الطّريقةُ 1: أقسمُ الشّكل المُركّب. أقسمُ الشّكل المُركّب إلى مُستطيلٍ ومُربّعٍ، ثُمّ أجدُ أبعاد الشّكلين النّاتجين.
|
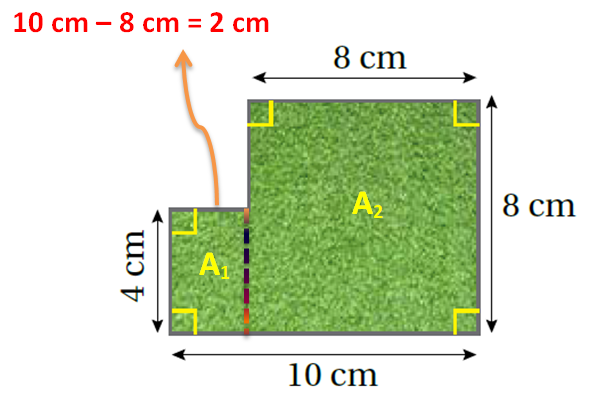 |
||||||||||
| إذن؛ مساحة الشكل الذي يُمثل الحديقة: | |||||||||||
|
الطّريقةُ 2: أستعملُ الطّرح. يُمكنُني حسابُ مساحة الشّكل المُركّب عن طريق طرح مساحة الجُزء المفقود (باللّون الأبيض) من مساحة المُستطيل الكبير.
إذن؛ مساحة الشكل الذي يُمثل الحديقة: |
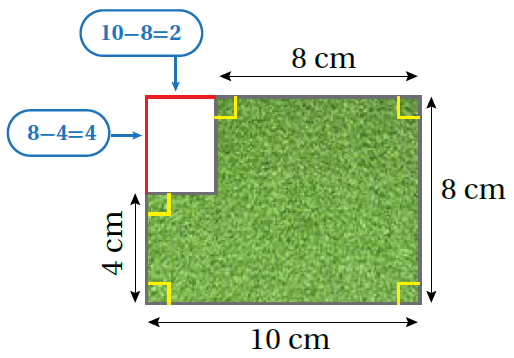 |
||||||||||
| ونلاحظُ أنّ الإجابة مُتساويةٌ في الطّريقتين. |