مساحة سطح المنشور والأسطوانة

مفاهيم أساسية :

المساحةُ الكلّيةُ لِسطحِ أيِّ مجسَّمٍ تساوي مجموعَ مساحاتِ أوجُهِهِ جميعِها 

المساحةُ الجانبيةُ لِسطحِ المنشورِ هِيَ مجموعُ مساحاتِ أوجُهِهِ الجانبيةِ. 

 

المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ المنشورِ:

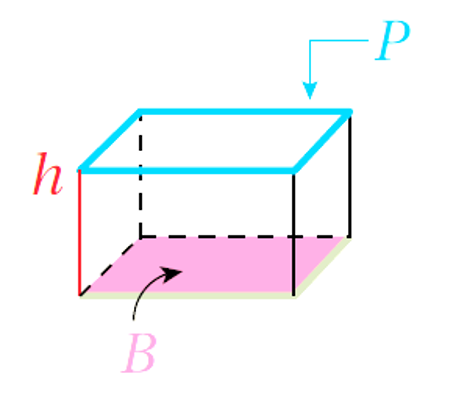
المساحةُ الجانبيةُ (L.A) لِسطحِ المنشورِ تساوي ناتجَ ضربِ ارتفاعِ المنشورِ (h) في محيطِ القاعدة (P)

L.A = Ph

 أمّا المساحةُ الكلّيةُ (S.A) لِسطحِ المنشورِ فَتُساوي مجموعَ مساحتِهِ الجانبيةِ وَمساحتَيْ قاعدتَيْهِ.

S.A = L.A + 2B

مثال 1: أَجِدُ المساحةَ الكلّيةَ لِسطحِ كلِّ منشورٍ ممّا يأتي:

1)

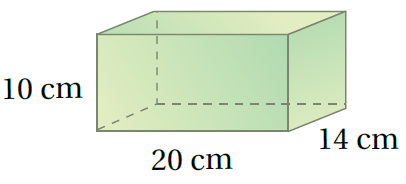
الْخُطْوَةُ 1:أَجِدُ محيطَ القاعدةِ:

           P = 2l + 2w                         محيط القاعدة المستطيلة  

P = 2(20) + 2(14)                         تعويض الأبعاد 

                  68 = P                         أَجِدُ الناتجَ

إذنْ، محيطُ القاعدةِ  68cm  

الْخُطْوَةُ 2: أَجِدُ المساحةَ الجانبيةَ لِسطحِ المنشورِ:

       L.A = Ph                                صيغة المساحة الجانبية لسطح المنشور 

68 × 10=                                      تعويض الأبعاد 

     680=                                       أَجِدُ الناتجَ

 إذنْ، المساحةُ الجانبيةُ لِسطحِ المنشورِ 680cm²

الْخُطْوَةُ 3: أَجِدُ مساحةَ القاعدةِ:

    B = l × w                                 مساحة القاعدة 

 20 × 14=                                    تعويض الأبعاد 

      280=                                     أَجِدُ الناتجَ

إذنْ، مساحةُ قاعدةِ المنشورِ 280cm²

الْخُطْوَةُ 4:أَجِدُ المساحةَ الكلّيةَ لِسطحِ المنشورِ:

      S.A = L.A + 2B                    صيغة المساحة الكلية لسطح المنشور 

(280)680+2=                           تعويض الأبعاد 

          1240 =                             أَجِدُ الناتجَ

إذنْ، المساحةُ الكلّيةُ لِسطحِ المنشورِ تساوي 1240cm²

 

يُمكنُنا استخدامُ قانونَيِ المساحةِ الجانبيةِ وَالمساحةِ الكلّيةِ لِسطحِ المنشورِ في مواقفَ حياتيةٍ كثيرةٍ ومتنوِّعةٍ.

مثال 2: منَ الحياةِ :ناطحاتُ سحابٍ: المبنى الظاهرُ في الصورةِ على شكلِ خماسيٍّ منتظمٍ ارتفاعُهُ 124m وَطولُ ضِلعِ قاعدتِهِ الخماسيةِ 41m ، أَجِدُ المساحةَ الجانبيةَ لِسطحِهِ.

بما أنَّ قاعدةَ المبنى على شكلِ خماسيٍّ منتظمٍ، إذنْ، محيطُ القاعدةِ يساوي ناتجَ ضربِ عددِ الأضلاعِ في طولِ الضِّلعِ الواحدِ.

  P = 5 × s                                 محيط القاعدة 

P = 5 × 41                                 تعويض الأبعاد 

    P = 205                                 أجد الناتج 

أجد المساحة الجانبية لسطح المبنى 

           L.A = Ph                       صيغة المساحة الجانبية لسطح المنشور                              

124×205 =                              تعويض الأبعاد 

    25420=                               أجد الناتج 

إذنْ، المساحةُ الجانبيةُ لِسطحِ المبنى إذنْ، المساحةُ الجانبيةُ لِسطحِ المبنى 25420m²

---

يُمكنُني إيجادُ المساحةِ الكلّيةِ للأُسطوانةِ عَنْ طريقِ شبَكتِها. فَعِندَ فتحِ أُسطوانةٍ، أَجِدُ أنَّ مساحةَ المستطيلِ الناتجِ يساوي المساحةَ الجانبيةَ لِلأُسطوانةِ، وَالمساحةَ الكلّيةَ لِسطحِها يساوي مجموعَ مساحتِها الجانبيةِ وَمساحتَيِ القاعدتَينِ.

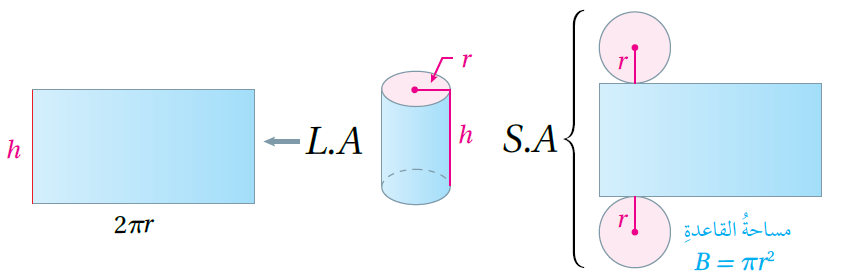
المساحةُ الجانبيةُ وَالمساحةُ الكلّيةُ لِسطحِ الأُسطوانةِ:

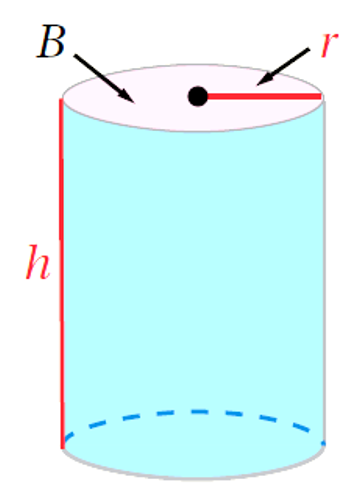
المساحةُ الجانبيةُ لِسطحِ الأُسطوانةِ هِيَ مساحةُ سطحِها المُنحني، وَتساوي حاصلَ ضربِ محيطِ قاعدتِها (P) في ارتفاعِها (h) .

$\mathbf{L}\mathbf{.}\mathbf{A}\mathbf{=}\mathbf{2}\mathbf{\pi rh}\mathbf{ }$ أو$\mathbf{ }\mathbf{L}\mathbf{.}\mathbf{A}\mathbf{=}\mathbf{\pi dh}$

المساحةُ الكلّيةُ لِلأُسطوانةِ فتساوي مجموعَ مساحتِها الجانبيةِ وَمساحتَيْ قاعدتَيْها. 

$\mathbf{S}\mathbf{.}\mathbf{A}\mathbf{=}\mathbf{ }\mathbf{L}\mathbf{.}\mathbf{A}\mathbf{+}\mathbf{2}\mathbf{B}$  أو $\mathbf{S}\mathbf{.}\mathbf{A}\mathbf{=}\mathbf{2}\mathbf{\pi h}\mathbf{+}\mathbf{2}{\mathbf{\pi r}}^{\mathbf{2}}$

 

مثال 3: أَجِدُ المساحةَ الجانبيةَ وَالمساحةَ الكلّيةَ لِسطحِ الأُسطوانةِ المجاورةِ. أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ مئة.

1)

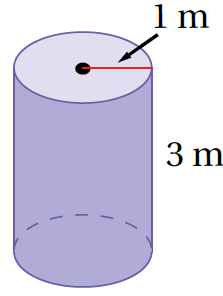
المساحة الجانبية :

      $\mathrm{L}.\mathrm{A}=2\mathrm{\pi rh}$                         صيغة المساحة الجانبية لسطح الأسطوانة 

$$\begin{gathered} =2\pi \left(1\right)\left(3\right) \\ \approx 18.85 \end{gathered}$$                               تعويض الأبعاد ، ثم أجد الناتج 

المساحة الكلية:

     $\mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+2{\mathrm{\pi r}}^2$                صيغة المساحة الكلية لسطح الأسطوانة 

$$\begin{gathered} \approx 18.85+2\pi {\left(1\right)}^2 \\ \approx 25.13 \end{gathered}$$                    تعويض الأبعاد ، ثم أجد الناتج 

إذنْ، المساحةُ الجانبيةُ لِسطحِ الأُسطوانةِ تساوي 18.85m² تقريبًا، وَالمساحةُ الكلّيةُ لَهُ تساوي 25.13m² تقريبًا

 

يُمكنُنا استخدامُ قانونَيِ المساحةِ الجانبيةِ وَالمساحةِ الكلّيةِ لِسطحِ الأُسطوانةِ في مواقفَ حياتيةٍ كثيرةٍ ومتنوعةٍ.

مثال 4: منَ الحياةِ:تغليفٌ: أرادَتْ لمياءُ تغليفَ الشمعةِ المجاورةِ هديةً لِصديقَتِها في عيدِ ميلادِها كَمْ سَنتيمترًا مربعًا على الأقلِّ تحتاجُ لمياءُ مِنَ ورقِ التغليفِ؟ أقرّبُ إجابتي لِأقربِ جزءٍ مِنْ عشرةٍ.

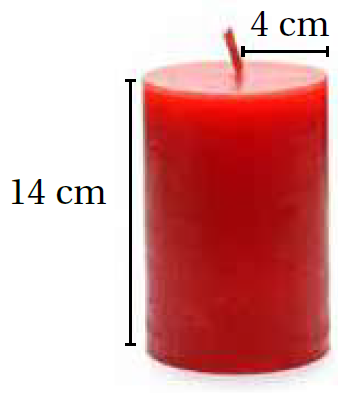
بِما أنَّ التغليفَ للشمعةِ كاملةً، إذنْ، أَجِدُ المساحةَ الكلّيةَ لِسطحِ الأُسطوانةِ:

المساحة الجانبية : 

        $\mathrm{L}.\mathrm{A}=2\mathrm{\pi rh}$                       صيغة المساحة الجانبية لسطح الأسطوانة 

$$\begin{gathered} =2\mathrm{\pi }\left(4\right)\left(14\right) \\ \approx 351.9 \end{gathered}$$                             تعويض الأبعاد ، ثم أجد الناتج 

المساحة الكلية :

       $\mathrm{S}.\mathrm{A}=\mathrm{L}.\mathrm{A}+2{\mathrm{\pi r}}^2$              صيغة المساحة الكلية لسطح الأسطوانة 

$$\begin{gathered} \approx 351.9+2\pi {\left(4\right)}^2 \\ \approx 452.4 \end{gathered}$$                  تعويض الأبعاد ، ثم أجد الناتج 

إذنْ، تحتاجُ لمياءُ تقريبًا 452.4cm²على الأقلِّ مِنَ الورقِ لِتغليفِ الشمعةِ.