رياضيات فصل أول

يكون الاقتران f(x) غير قابل للاشتقاق عند x = a، في الحالات التالية اذا كان f(x) له :

* رأس حاد عند x = a.

* زاوية عند x = a.

* مماس رأسي عند x = a.

* اذا كان f(x)  غير متصل عند x = a.

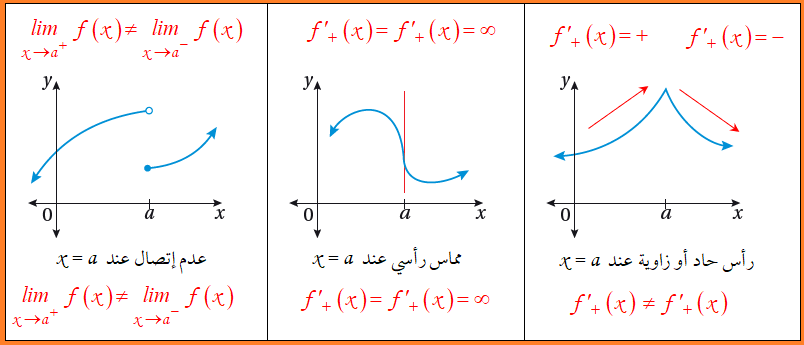
نستنتج أن اذا كان f(x) قابلا للاشتقاق عند x = a، فإنه متصل عند x = a.

قوانين اللوغاريتمات:
اذا كانت b, x, y أعداداً حقيقيةً موجبةً، و كان p عدداً حقيقياً، حيث $b\ne 1$، فإن:

1. قانون الضرب: $lo{g}_b\left(xy\right)= lo{g}_b\left(x\right)+lo{g}_b\left(y\right)$

2. قانون القسمة: $lo{g}_b\left(x/y\right)= lo{g}_b\left(x\right)-lo{g}_b\left(y\right)$

3. قانون القوِّة: $lo{g}_b\left(x^p\right)= p lo{g}_b\left(x\right)$

---

v(t) = اشتقاق اقتران الموقع s(t) مرة واحدة.

a(t) = اشتقاق اقتران الموقع s(t) مرتين.