رياضيات أدبي فصل أول

مضروب العدد 

يُمكِن التعبير عن 1 × 2 × 3 باستعمال الرمز ! 3 الذي يُقرَأ : مضروب العدد ثلاثة.

مفهوم أساسي (مضروب العدد)

بالكلمات : مضروب العدد الصحيح الموجب n هو حاصل ضرب الأعداد الصحيحة الموجبة التي هي أصغر من (أو تساوي) n .

بالرموز  : n! = n × (n - 1) × (n - 2) × . . . × 1

 

مثال : 

أجد ناتج كلٍّ ممّا يأتي : 

$a) 4! b) (7 -2)! c) 3! +2! d) \frac{7! }{5! }$

الحل : 

$a) 4! = 4 \times 3 \times 2 \times 1 = 24$

 

$b) (7 - 2)! = 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$

 

$c) 3! + 2! = (3 \times 2 \times 1) + (2 \times 1) = 8$

 

$d) \frac{7!}{5!}= \frac{7 \times 6 \times \cancel{ 5!}}{\cancel{5!}} = 42$

 

---

ورقة التقييم الأول :

ضع دائرة حول رمز الإجابة الصحيحة في كل مما يأتي : 

1) الزوج المُرتَّب الذي يُمثِّل حَلًّا للمتباينة :  $x - 4y \le 2$  ، هو : 

$a) (5 , -1) b) (4 , 0) c) (3 , -1) d) (-1 , 1)$

الحل : 

$x - 4y \le 2-1 - 4\left(1\right) \stackrel{?}{\le 2}-5 \le 2$

 

---

2)  المتباينة التي يكون الزوج المُرتَّب (3 , 5-) حَلًّا لها هي : 

$a) 3x + 2y>-1 b) 1-2x \ge 11 c) x-y <-8 d y -x <5$

الحل : 

$1 - 2x \ge 111 - 2(-5) 1 + 10 = 11 11 \ge 11$

---

3) المتباينة التي لها التمثيل البياني الآتي هي : 

$a) 5x-y>4 b) 5x -y <-4 c) x-4y <1 d) y-2x<5$

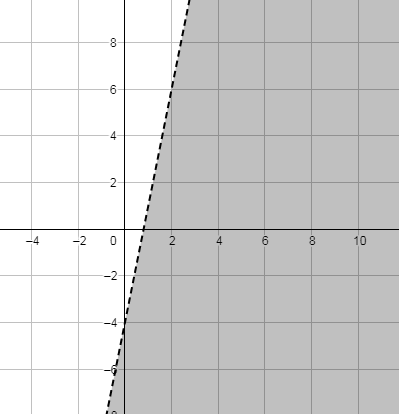
الحل : 

أجد معادلة المستقيم الحدودي 

$m = \frac{y_2-y_1}{x_2-x_1}= \frac{-4-6}{0-2} = 5y = mx + b y = 5x -4 \Rightarrow 5x - y = 4$

أختبر نقطة في منطقة الحل ، ولتكن (0 ، 2) 

$5\left(2\right) - 0 = 10 10 > 4$

 إذن المتباينة $5x - y > 4$ولا يحتوي رمز المتباينة على المساوة لأن المستقيم الحدودي منقط . 

---

 

4) الزوج المرتب الذي يُمثل حلّا لنظام المتباينات الآتي هو :   $6x - 3y \le 2 , 4x + 0.5 y > 2$

      $a) (1 , -1) b) (2 , 4) c) (4 , 2) d) (-1 , 1)$

 

الحل : 

$6x - 3y \le 26\left(2\right)-3\left(4\right) = 0 \le 24x + 0.5 y > 24\left(2\right)+ 0.5\left(4\right) =10 > 2$

---

5) نظام المتباينات الذي له التمثيل البياني الآتي ، هو: 

$a) 2x-y>2 , x \le 1 b) x+y >1 , x \ge 1 c) x-y >1 , x > 1 d) y-x<1 , x \ge 1$

 

الحل  : 

معادلة المستقيم المائل  y = 1 - x   ، إذن  y + x = 1  ، وباختبار نقطة مثل (2 ، 0) 

$2 + 0 = 2 > 1$  إذن المتباينة هي  :  y + x  > 1  ويوضع رمز المتباينة بدون مساواة لأن المستقيم متقطع 

معادلة المستقيم الموازي لمحور y  هو  x = 1  ، ولأنّ منطقة الحل يمين العدد  1 ، إذن المتباينة هي: $x \ge 1$

---

6) ماعدد الطرائق المُمكِنة لتكوين عدد من ثلاث منازل من الأرقام : 1 ، 3 ، 5 ، 7  إذا لم يُسمح بالتكرار ؟ 

$a) 128 b) 105 c) 24 d) 12$

الحل  : 

$4 \times 3 \times 2 \times 1 = 24$

---

7) يُقدم مطعم 3 أصناف من اللحوم و4 أصناف من الشوربات و 4 أصناف من المقبلات ، بكم طريقة يُمكن اختيار وجبة تحتوي على طبق لحوم وطبق شوربة وطبق مقبلات ؟

$a) 48 b) 36 c) 24 d) 12$

الحل  : 

$3 \times 4 \times 4 = 48$

---

8) بكم طريقة يُمكِن اختيار نوعين من الأقلام من بين 5 أنواع مختلفة ، ونوعين من الدفاتر  من بين 6 أنواع مختلفة ، إذا سُمح بتكرار  أنواع الأقام فقط  ؟ 

$a) 900 b) 750 c) 600 d) 450$

الحل  : 

$5 \times 5 \times 6 \times 5 = 750$

---

9) ما عدد الطرق التي يمكن بها تكوين كلمة من ثلاثة أحرف وليس بالضرورة أن يكون للكلمة معنى من الأحرف : ق ، م ،  ر  ، ي ، ن  إذا كان الحرف الأول ي وسُمح بتكرار باقي الأحرف ؟

$a) 125 b) 60 c) 24 d) 16$

الحل  : 

$1 \times 4 \times 4 = 16$

---

10) أجد إحداثيي النقطة ( x, y ) التي تجعل الاقتران: C = 3x +5y أقل ما يُمكِن ضمن القيود الآتية :

$x + 2y > 52x + y \ge 4x \ge 0 , y \ge 0$

الحل  : 

C = 3x +5y	رؤوس منطقة الحلول المُمكنة
C = 3(0) + 5(4) = 20	A (0 , 4)
C = 3(1) + 5(2) =  13	B (1 , 2)
Q = 3(5) + 4(0) = 15	C (5 , 0)

إذن  إحداثيي النقطة ( x, y ) التي تجعل الاقتران: C = 3x +5y أقل ما يُمكِن هي (2 ، 1) 

---

 

11)   يُنتِج أحد المصانع نوعين  من الشوكولاتة ، ويحقق ربحًا مقداره JD 2 عن كل علبة مبيعة من النوع الأول ، و JD 3  عن كل علبة مبيعة من النوع الثاني. إذا كان عدد العلب المُنتجة من كلا النوعين لا يزيد عن 900 علبة شهريًا ، وأنّ عدد علب الشوكولاتة المنتجة من النوع الثاني أقل من أو يساوي 300 علبة شهريًا مضافًا إليه مثلي عدد العلب من النوع الأول . كم علبة شوكولاتة من كل نوع يجب أنْ يُنتِج المصنع شهريًّا لتحقيق أكبر ربح مُمكن ، مُفترِضًا بيع الإنتاج كاملًا كل شهر؟ 

الحل  : 

 أفرض عدد العلب من الشوكولاتة من النوع الأول = x ، وعدد العلب من الشوكولاتة من النوع الثاني = y 

يريد المصنع تحقيق أكبر قيمة لاقتران الربح  :  P = 2 x + 3y 

في ظل القيود الآتية : 

$𝑥 + 𝑦 \le 900 y-2x\le 300x\ge 0 , y \ge 0$

P = 2 x + 3y	رؤوس منطقة الحلول المُمكنة
P = 2(0)+ 3(0) = 0	A (0 , 0)
P = 2(0)+ 3(300) = 900	B (0 , 300)
P = 2(900)+ 3(0) = 900	C (900 , 0)
P = 2(200)+ 3(700) = 2500	D (200 , 700)

 

 

 

 

 

أُلاحظ من الجدول أنَّ أكبر قيمة ممكنة لاقتران الهدف هي 2500 ، وهذه القيمة تتحقق عندما x = 200 ، y = 700 

 

---

12) ترغب سيدة في شراء ثلاجة ، فذهبت إلى أحد محال بيع الأجهزة الكهربائية  ، ووجدت فيه 3 أنواع مختلفة من الثلاجات، لكل نوع منها لونان : أسود ، وأبيض ، وفضي ،أجد عدد الطرائق المُمكِنة لشراء السيدة ثلاجة باستخدام : 

1) المُخطَّط الشجري.                                   2) الجدول.                                                    3) القائمة المنظمة.

الحل  : 

أفرض أنواع الثلاجات : 1 ، 2 ، 3    ،  وألوان الثلاجات : S , B , W 

1)  المُخطَّط الشجري. 

عدد الطرق = 9 

---

2) الجدول.  
   

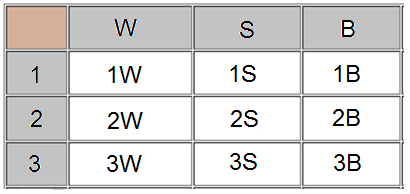
 عدد الطرق = 9

---

3) القائمة المنظمة.

---