رياضيات فصل أول

أتحققُ من فهمي(1)

1) أكتبُ معادلةَ المستقيمِ الذي ميلُه 5 والمقطعُ y لهُ 2- بصيغةِ المَيلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 5x + (-2) \\ y=5x -2 \end{gathered}$$

2) أجدُ معادلةَ المستقيمِ المارِّ بالنقطةِ $( -1, 0)$ وميلُه $\frac{1}{3}$بصيغةِ المَيلِ والمقطعِ

$$\begin{gathered} y=mx+b \\ y= \frac{1}{3}x +b \\ 0=\frac{1}{3}(-1) +b \\ b=\frac{1}{3} \\ \Rightarrow y = \frac{1}{3}x+\frac{1}{3} \end{gathered}$$

3) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطتينِ ( 4-, 0) و ( 6 , 2-) بصيغةِ المَيلِ والمقطعِ.

$$\begin{gathered} b=-4 \\ m=\frac{-4-6}{0--2}=\frac{-10}{2}=-5 \\ y=mx+b \\ y=-5x-4 \end{gathered}$$

أتحققُ من فهمي(2)

1) $y=2x+1$

2) $y=x-4$

3) $$\begin{gathered} y=3-x \\ y=-x+3 \end{gathered}$$

 

أتحققُ من فهمي(3)

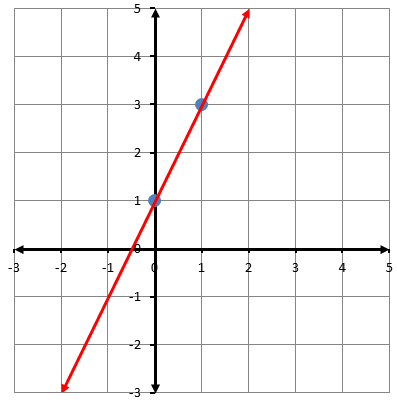
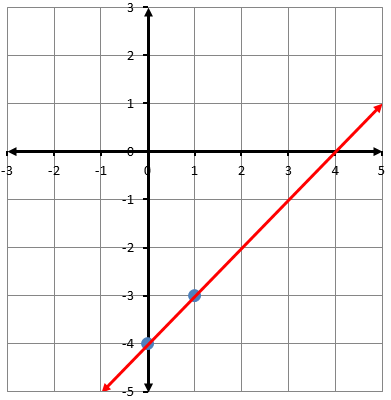
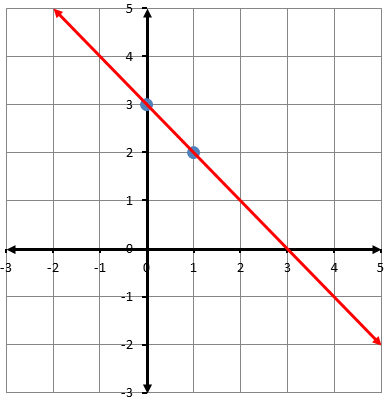
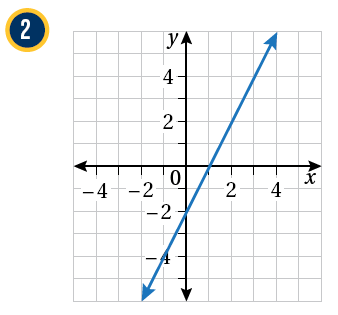
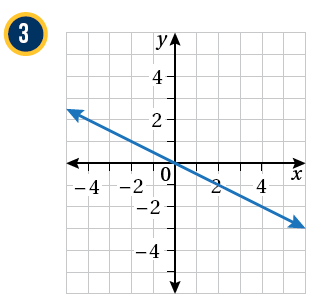
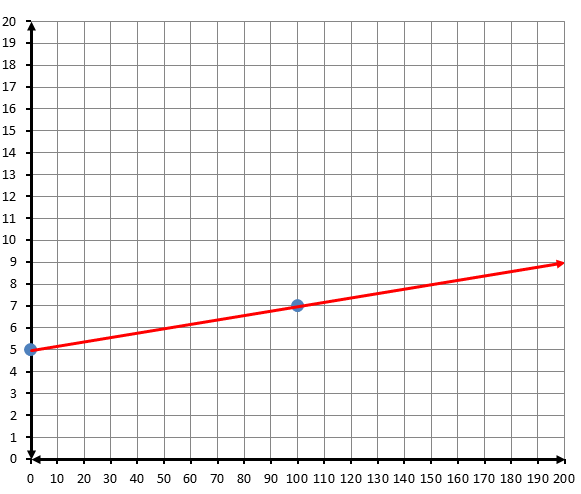
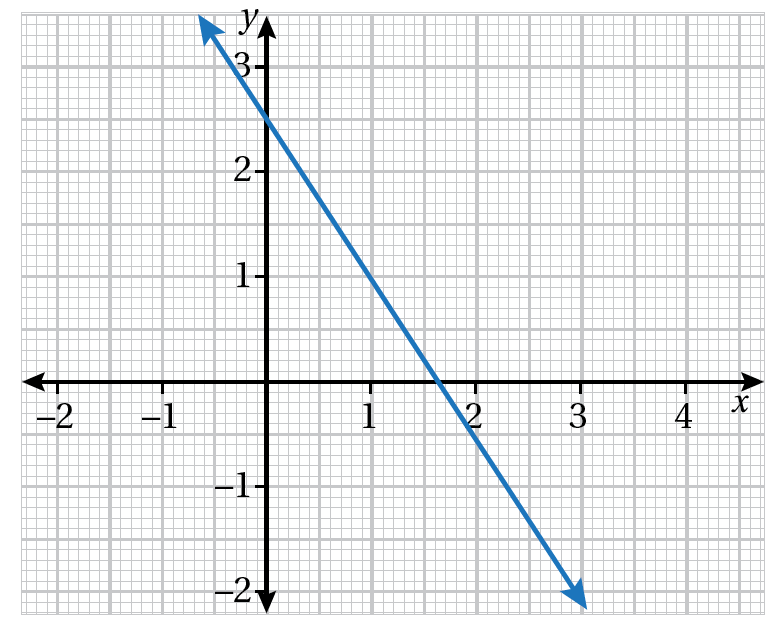
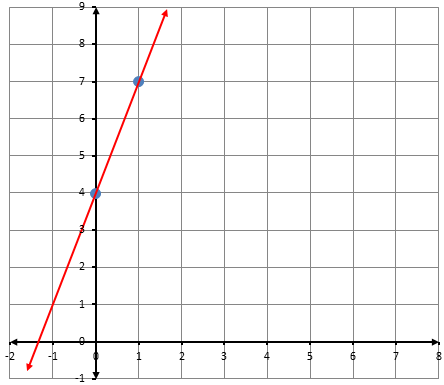
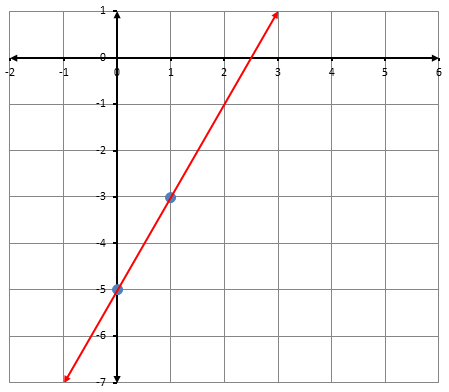
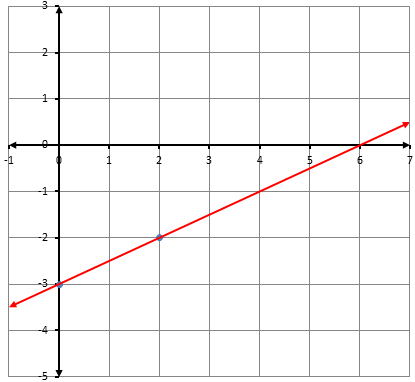
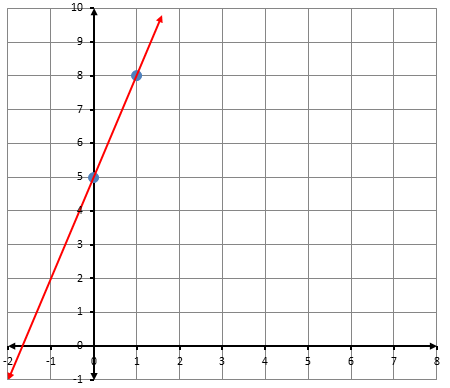
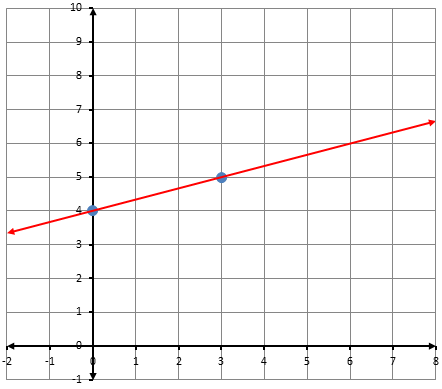
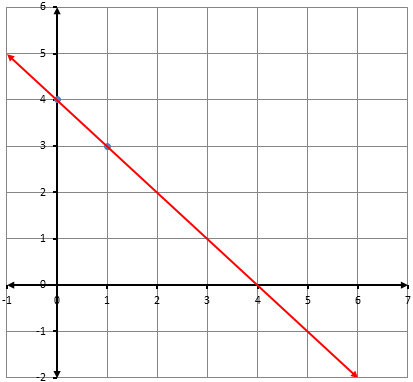
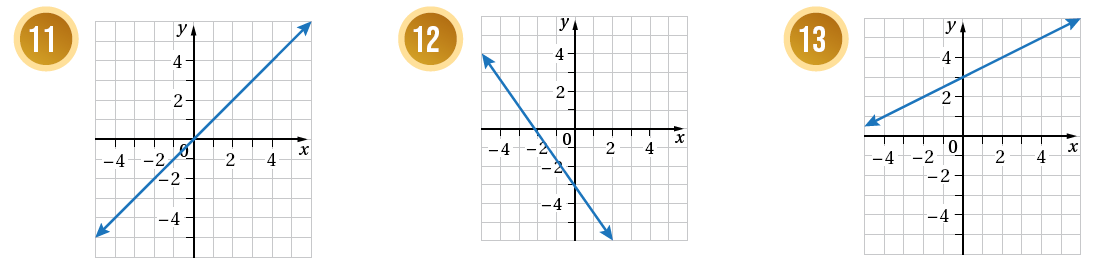
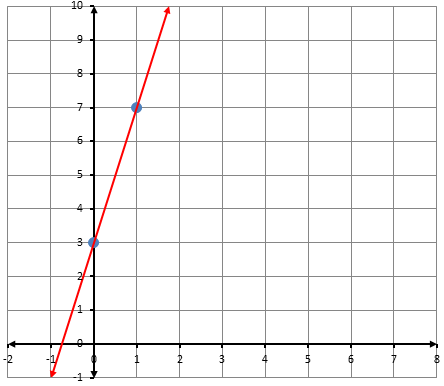
أكتبُ معادلةَ المستقيمِ الممثَّلِ بيانيًّا في كلِّ شكلٍ ممّا يأتي بصيغةِ الميلِ والمقطعِ:

   

  $$\begin{gathered} b=-2 \\ (0, -2) , (1, 0) \\ m=\frac{0--2}{1-0}=2 \\ y=mx+b \\ y= 2x-2 \end{gathered}$$

 

 

 

 

 

 $$\begin{gathered} b=0 \\ (0, 0) , (2, -1) \\ m=\frac{-1-0}{2-0}=\frac{-1}{2} \\ y=mx+b \\ y= \frac{-1}{2}x+0 \\ y=\frac{-1}{2}x \end{gathered}$$

 

أتحققُ من فهمي(4) 

اشتراكُ هاتفٍ: تدفعُ فرحُ اشتراكًا شهريًّا لهاتفِها قيمتُه 5 دنانيرَ، وتدفعُ قرشينِ عنْ كلِّ دقيقةٍ
تتحدثُ فيها بالهاتفِ.

1) أكتبُ معادلةً خطيّةً بمتغيرينِ لإيجادِ تَكلِفةِ ما تدفعُه فرحُ عندَ تحدُّثِها عددًا منَ الدقائقِ خلالَ الشهرِ.

$y=0.02x+5$

2) أصفُ ما يمثّلُه المقطعُ y والميلُ في المسألةِ.

المقطع $y$ يساوي 5، وهي قيمة الاشتراك الشهري الثابت، أما الميل فيمثل نسبة الزيادة على قيمة الاشتراك بنسبة ثابتة حسب عدد الدقائق

3) أجدُ المقطعَ x للمعادلةِ، ثمَّ أصفُ ما يمثّلُه في المسألةِ.

قيمة المقطع $x$ تساوي $-250$ وحيث أن $x$ تمثل زمن لذا فتعتبر قيمة مرفوضة وعليه لا يوجد مقطع $x$ لهذه المعادلة 

4) أمثّلُ المعادلةَ بيانيًّا باستعمالِ الميلِ والمقطعِ .

أتحققُ من فهمي(5) 

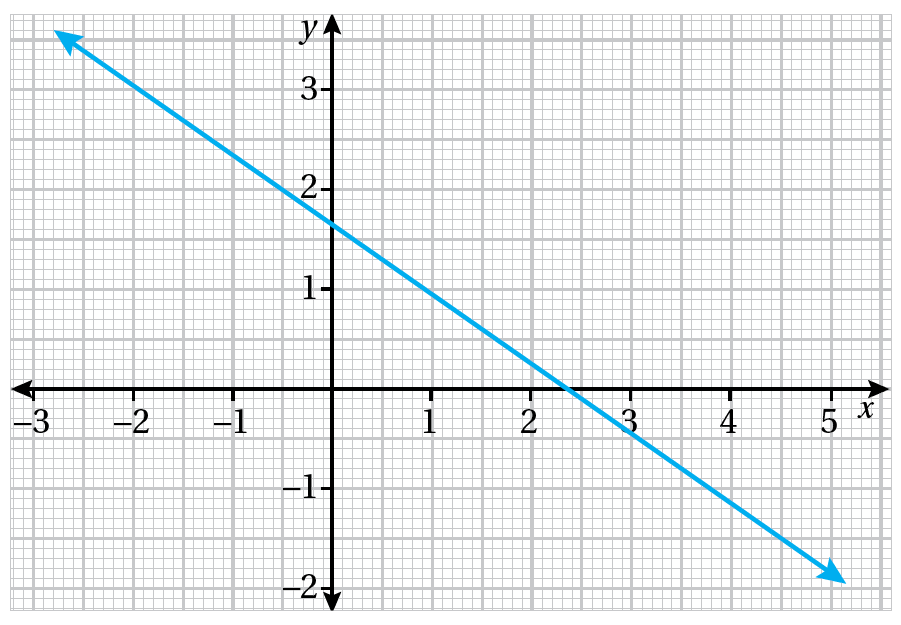
يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ للمعادلةِ  $y = 2.45 - 1.37x$. أستعملُ التمثيلَ البيانيَّ لأجدَ حلَّ كلِّ معادلةٍ ممّا يأتي:

1) $2.45 - 1.37x = 0$

$x= 1.7$

2) $2.45 - 1.37x = 3$

$x=-0.4$

3) $2.45 = 1.37x - 1.5$

$x=2.6$

 

أتدرب وأحل المسائل

1)أكتبُ معادلةَ المستقيمِ الذي ميلُه 1 والمقطعُ y لهُ 1- بصيغةِ الميلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 1x + (-1) \\ y=x -1 \end{gathered}$$

2) أجدُ معادلةَ المستقيمِ المارِّ بنقطةِ الأصلِ وميلُه 4 بصيغةِ الميلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 4x + \left(0\right) \\ y=4x \end{gathered}$$

3) أكتبُ معادلةَ المستقيمِ المارِّ بالنقطتينِ ( 4 , 2-) و ( 1-, 3) بصيغةِ الميلِ والمقطعِ.

$$\begin{gathered} m=\frac{4--1}{-2-3}=\frac{5}{-5}=-1 \\ y=mx+b \\ y= -1x +b \\ 4=-1(-2) +b \\ 4=2+b \\ b=2 \\ \Rightarrow y=-1x+2 \end{gathered}$$

4) أكتبُ معادلةَ المستقيمِ الأفقيِّ الذي يقطعُ المحورَ y في النقطةِ ( 5-, 0) بصيغةِ الميلِ والمقطعِ.

$$\begin{gathered} y=mx+b \\ y= 0x +(-5) \\ \Rightarrow y = -5 \end{gathered}$$

أمثلُ كلَّ معادلةٍ ممّا يأتي بيانيًّا باستعمالِ الميلِ والمقطعِ $y$:

5) $y = 3x + 4$

6) $y = 2x - 5$

7) $y=\frac{x}{2}-3$

8) $y = 3x + 5$

9) $y=\frac{x}{3}+4$

10) $y = 4 - x$
      $y=-x+4$

أكتبُ معادلةَ المستقيمِ المُمثَّلِ بيانيًّا في كلٍّ ممّا يأتي بصيغةِ الميلِ والمقطعِ:

           $$\begin{gathered} b=0 \\ (0, 0) , (2, 2) \\ m=\frac{2-0}{2-0}=\frac{2}{2}=1 \\ y=mx+b \\ y= 1x+0 \\ y=x \end{gathered}$$                 $$\begin{gathered} b=-3 \\ (0, -3) , (-2, 0) \\ m=\frac{0--3}{-2-0}=\frac{3}{-2}=-1.5 \\ y=mx+b \\ y= \frac{-3}{2}x+-3 \\ y=-1.5x-3 \end{gathered}$$               $$\begin{gathered} b=3 \\ (0, 3) , (2, 4) \\ m=\frac{4-3}{2-0}=\frac{1}{2} \\ y=mx+b \\ y= \frac{1}{2}x+3 \end{gathered}$$

 

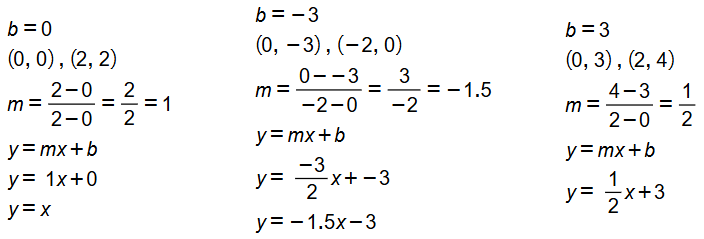
أشجارٌ: يبيّنُ التمثيلُ البيانيُّ المجاورُ 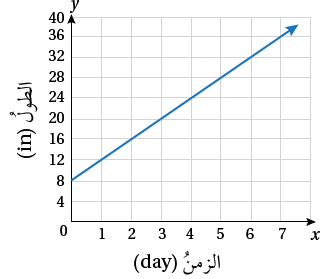العلاقةَ بينَ طولِ نبتةِ موزٍ بالإنشِ والزمنِ بالأيامِ منذُ زراعتِها.

14) كمْ كانَ طولُ الشجرةِ عندَ زراعتِها؟

8 أمتار 

15) أكتبُ معادلةً خطيةً بمتغيرَينِ تمثلُ مقدارَ نموِّ شجرةِ الموزِ بعدَ مرورِ أيامٍ عدّةٍ.

$$\begin{gathered} b=8 \\ (0, 8) , (1, 12) \\ m=\frac{12-8}{1-0}=4 \\ y=mx+b \\ y= 4x+8 \end{gathered}$$

16) بيئةٌ: تتناقصُ انبعاثاتُ أولِ أكسيدِ الكربونِ في جميعِ أنحاءِ العالمِ بنحوِ 2.6 مليون طنٍّ متريٍّ كلَّ عامِ. ففي عامِ 1991 بلغتِ انبعاثاتُ أولِ أكسيدِ الكربونِ 79 مليونَ طنٍّ متريٍّ. أكتبُ معادلةً خطيةً بمتغيرينِ تمثّلُ العلاقةَ بينَ انبعاثاتِ أولِ أكسيدِ الكربونِ والزمنِ. (إرشادٌ: أفترضُ أنَّ x = 91 تدلُّ على العامِ 1991).

$$\begin{gathered} \mathit{y}\mathbf{=}\mathit{m}\mathit{x}\mathbf{+}\mathit{b} \\ \mathit{y}\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{6}\mathit{x}\mathbf{+}\mathit{b} \\ \mathbf{79}\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{6}\mathbf{*}\mathbf{91}\mathbf{+}\mathit{b} \\ \mathbf{79}\mathbf{=}\mathbf{ }\mathbf{-}\mathbf{236}\mathbf{.}\mathbf{6}\mathbf{+}\mathit{b} \\ \mathit{b}\mathbf{=}\mathbf{315}\mathbf{.}\mathbf{6} \\ \mathit{y}\mathbf{=}\mathbf{-}\mathbf{2}\mathbf{.}\mathbf{6}\mathit{x}\mathbf{+}\mathbf{315}\mathbf{.}\mathbf{6} \end{gathered}$$

 

17) علومُ الأرضِ: أعودُ إلى فِقْرةِ (أستكشفُ) بدايةَ الدرسِ، وأحلُّ المسألةَ.

أستكشفُ
يبلغُ متوسطُ درجةِ الحرارةِ على سطحِ الأرضِ $20 c°$ تقريبًا. وترتفعُ درجةُ الحرارة تحتَ سطحِ القشرةِ الأرضيةِ بمعدلِ $25 C°$ لكلِّ كيلومترٍ منَ العمقِ. أكتبُ معادلةً بمتغيرينِ تمثّلُ درجةَ الحرارةِ لكلِّ كيلومترٍ تحتَ سطحِ الأرضِ.

$y= 20 +25x$

 

يبيّنُ الشكلُ الآتي التمثيلَ البيانيَّ للمعادلةِ 2.7y + 1.9x = 4.42 . أستعملُ التمثيلَ البيانيَّ لأجدَ حلَّ كلِّ معادلةٍ ممّا يأتي:  

18) 1.9x = 4.42

$y= 0 , x=2.4$

19) 2.7y = 4.42

$x=0, y=1.7$

20) 2.7 + 1.9x = 4.42

$y=1, x=1$

21) 2.7y + 3.8 = 4.42

$x=2, y=0.3$

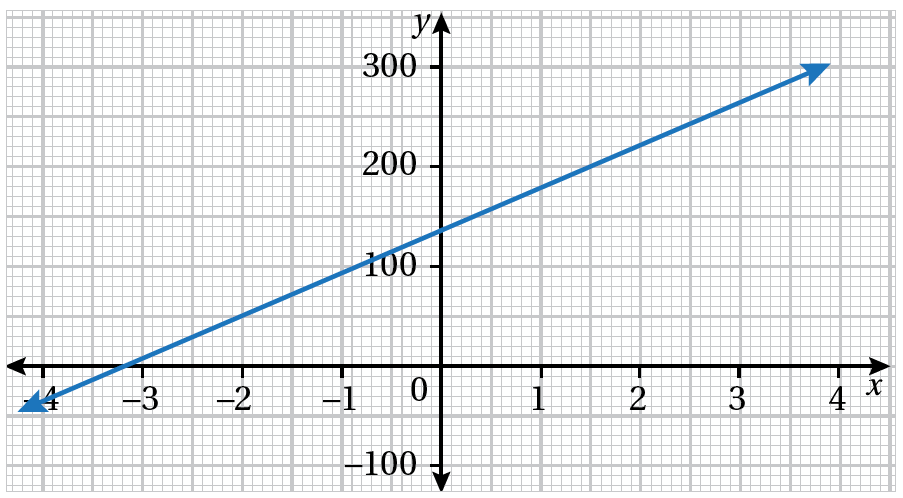
22) تبريرٌ: يبيّنُ الشكلُ المجاورُ التمثيلَ البيانيَّ للمعادلةِ y = 43.8x + 136.2 . أستعملُ التمثيلَ البيانيَّ لأجدَ حلَّ المعادلةِ 438x + 1362 = 1500 ، مبرّرًا إجابتِي

المعادلة الثانية تساوي المعادلة الأولى مضروباً في 10

$y= 150, x=0.3$

23) أكتشفُ المختلفَ: أيُّ المعادلاتِ الآتيةِ مختلفةٌ؟ أبرّرُ إجابتي.

المعادلة المختلفة هي المعادلة $3x-2y=12$، لأن الميل لهذه المعادلة يساوي $\frac{3}{2}$ أما ميل باقي المعادلات فيساوي $\frac{-2}{3}$

 24) تحدٍّ: أجدُ قيمةَ $a$ في المعادلةِ $2y + ax = -5$ ، علمًا أنَّ ميلَ المعادلةِ $\frac{5}{2}$

$$\begin{gathered} 2y+ax=-5 \\ 2y=-ax-5 \\ y= \frac{-a}{2}-\frac{5}{2} \\ m=\frac{-a}{2}=\frac{5}{2} \\ \Rightarrow a=-5 \end{gathered}$$

25) أكتبُ: كيفَ أكتبُ معادلةَ مستقيمٍ بصيغةِ الميلِ والمقطعِ عُلم ميلُه والمقطعُ y لهُ.

صيغةُ الميلِ والمقطعِ للمعادلةِ الخطّيّةِ هيَ: ،$y = mx + b$ حيثُ m مَيلُ المستقيمِ، و b المقطعُ y لهُ

 

كتاب التمارين 

يمرُّ المستقيمُ الّذي يمثلُ المعادلةَ y = 4x + c في النقطةِ : $( 1, 7)$

1) أجدُ قيمةَ $c$.

$$\begin{gathered} y=4x+c \\ 7=4\left(1\right)+c \\ c=3 \\ \Rightarrow y=4x+3 \end{gathered}$$

2) أمثلُ المعادلةَ بيانيًّا باستعمالِ الميلِ والمقطعِ $y$.

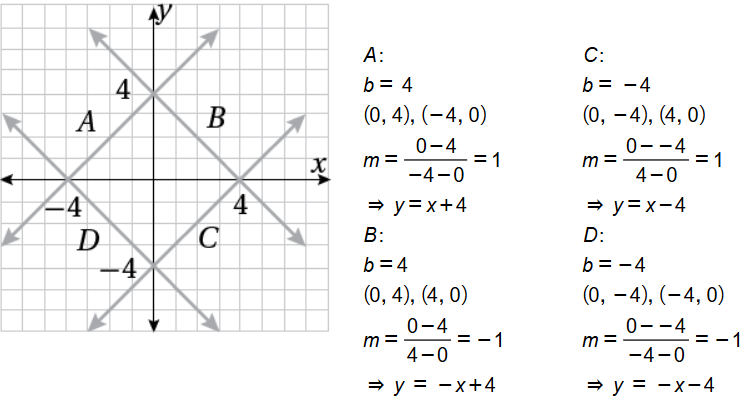
3) يبيّنُ التمثيلُ البيانيُّ المجاورُ المستقيماتِ A, B, C, D . أكتبُ معادلةَ كلِّ مستقيمٍ بصيغةِ الميلِ والمقطعِ. 

      $$\begin{gathered} A: \\ b= 4 \\ (0, 4), (-4, 0) \\ m=\frac{0-4}{-4-0}=1 \\ \Rightarrow y=x+4 \\ B: \\ b=4 \\ (0, 4), (4, 0) \\ m=\frac{0-4}{4-0}=-1 \\ \Rightarrow y = -x+4 \end{gathered}$$                $$\begin{gathered} C: \\ b= -4 \\ (0, -4), (4, 0) \\ m=\frac{0--4}{4-0}=1 \\ \Rightarrow y=x-4 \\ D: \\ b=-4 \\ (0, -4), (-4, 0) \\ m=\frac{0--4}{-4-0}=-1 \\ \Rightarrow y = -x-4 \end{gathered}$$

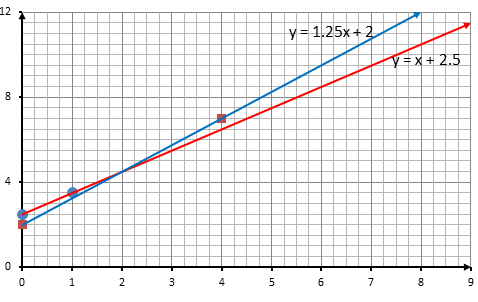
تستعملُ شركةُ النقلِ البرّيِّ A المعادلةَ C = 2.5 + k لحسابِ تكلفةِ الرحلةِ (بالدينار) لكلِّ k كيلومترًا. وتستعملُ شركةُ النقلِ البرّيِّ B المعادلةَ C = 2 + 1.25 k لحسابِ تكلفةِ الرحلةِ (بالدينارِ) لكلِّ k كيلومترًا:
4) أستعملُ المستوى الإحداثيَّ المجاورَ لتمثيلِ المعادلتَينِ بيانيًّا باستعمالِ الميلِ والمقطعِ . y

5) ما طولُ الرحلةِ الّتي تتقاضى عليها الشركتانِ المبلغَ نفسَهُ؟

$2 km$

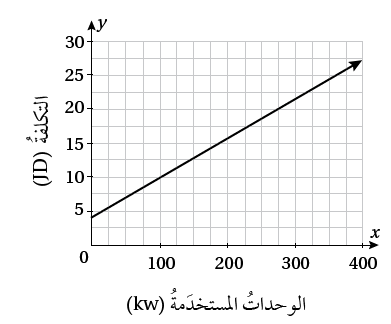
يبيّنُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بَيْنَ التكلفةِ الكلّيةِ وعددِ وحداتِ الطاقةِ الكهربائيةِ المستخدَمةِ: 

6) أجدُ قيمةَ المقطعِ y، ثُمَّ أصفُ ما يمثلُهُ في المسألةِ.

المقطع $y$ يساوي 4 وهي أقل تكلفة ممكنة حت في حال عدم استخدام الكهرباء

7) أجدُ ميلَ المستقيمِ، ثُمَّ أصفُ ما يمثلُهُ في المسألةِ.

$$\begin{gathered} (100, 10), (275, 20) \\ m= \frac{20-10}{275-100}=\frac{10}{175} \end{gathered}$$

يمثل نسبة الزيادة الثابتة حيث يمكن القول أنها 10 دنانير لكل 175 كيلوواط

8) أكتبُ معادلةً خطيةً بمتغيرَينِ لإيجادِ التكلفةِ الكليةِ لوحداتِ الطاقةِ الكهربائيةِ المستخدَمةِ.

$\mathit{y}\mathbf{=}\frac{\mathbf{10}}{\mathbf{175}}\mathit{x}\mathbf{+}\mathbf{4}$

---