الدرس الأول: مفهوم القسمة
الكلمات المفتاحية 
القسمة
أستكشف 
وَزَّعَتْ سَلْمى 40 قَلَمًا عَلى إِخْوَتِها الْأَرْبَعَةِ بِالتَّساوي. كَمْ قَلَمًا أَخَذَ كُلٌّ مِنْهُمْ؟
ألاحظ أن في أن عدد الأقلام 40، وعدد الأخوة 4، المطلوب توزيع الأقلام بالتساوي، يعني أن كل أخ يجب أن يكون معه عدد من الأقلام مساو لما مع الآخرين.
وهذا يتطلب التوزيع على مراحل ضمن مجموعات متساوية.
 سوف نتعلم في هذا الدرس مفهوم القسمة هي أن القسمة مجموعات متساوية لإيجاد عدد المجموعات أو عدد الأشياء في كل مجموعة.
سوف نتعلم في هذا الدرس مفهوم القسمة هي أن القسمة مجموعات متساوية لإيجاد عدد المجموعات أو عدد الأشياء في كل مجموعة.
أتعلم 
 عِنْدَ تَقْسيمِ عَدَدٍ مِنَ الْأَشْياءِ الْمُتَوافِرَةِ لَدَيَّ إِلى مَجْموعاتٍ مُتَساوِيَةٍ، أَسْتَعْمِلُ الْقِسْمَةَ لِأَجِدَ عَدَدَ الْمَجْموعاتِ أَوْ عَدَدَ الأَشْياءِ في كُلِّ مَجْموعَةٍ..
عِنْدَ تَقْسيمِ عَدَدٍ مِنَ الْأَشْياءِ الْمُتَوافِرَةِ لَدَيَّ إِلى مَجْموعاتٍ مُتَساوِيَةٍ، أَسْتَعْمِلُ الْقِسْمَةَ لِأَجِدَ عَدَدَ الْمَجْموعاتِ أَوْ عَدَدَ الأَشْياءِ في كُلِّ مَجْموعَةٍ..
أولا الْقِسْمَةُ كَمَجْموعاتٍ مُتَساوِيَةٍ
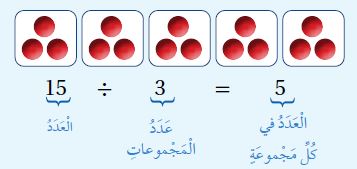
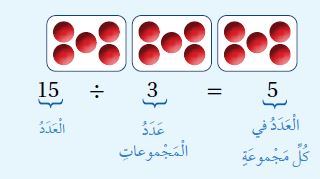
إِذا قَسَّمْتُ 15 قِطْعَةَ عَدٍّ إِلى مَجْموعاتٍ في كُلٍّ مِنْها 3 قِطَعٍ، فَما عَدَدُ الْمَجْموعاتِ؟
أُكَوِّنُ مَجْموعاتٍ ثُلاثِيَّةً مِنَ قِطَعِ الْعَدِّ، ثُمَّ أَعُدُّ الْمَجْموعاتِ النّاتِجَةَ.
أُلاحِظُ أَنَّ عَدَدَ الْمَجْموعاتِ يُساوي 5
يتبين أن هناك مجموعات ، وهذه المجموعات متساوية مما يعني أن تحوي نفس العدد من القطع (3 قطع.)
أقوم بعد المجموعات المتكونة لدي، أجد أنها 5 مجموعات.
 وهكذا تكون مسألة القسمة:
وهكذا تكون مسألة القسمة:
 15 هي عدد القطع جميعها
15 هي عدد القطع جميعها
 3 عدد القطع في كل مجموعة
3 عدد القطع في كل مجموعة
 إشارة القسمة
إشارة القسمة
 5 هو الناتج والذي يمثل عدد المجموعات
5 هو الناتج والذي يمثل عدد المجموعات
ثانيا الْقِسْمَةُ كَمُشارَكَةٍ بِالتَّساوي
•إِذا قَسَّمْتُ 15 قِطْعَةَ عَدٍّ إِلى 3 مَجْموعاتٍ مُتَساوِيَةٍ، فَكَمْ قِطْعَةَ عَدٍّ في كُلِّ مَجْموعَةٍ؟
أُوَزِّعُ قطِعَةَ عَدٍّ واحِدَةً في كُلِّ مَرَّةٍ عَلى الْمَجْموعَةِ حَتىّ تَنتْهَيَ قِطَعُ العَدِّ ، ثُمَّ أَجِدُ عَدَدَ الْقِطَعِ في الْمَجْموعَةِ كُلِّها.
أُلاحِظُ أَنَّ عَدَدَ الْقِطَعِ في كُلِّ مَجْموعَةٍ يُساوي 5
في هذه المسألة لأعرف عدد القطع التي تحويها كل مجموعة من المجموعات الثلاث
أقوم بالتوزيع قطعة في كل مرة على كل مجموعة، إلى أن ينتهي عد جميع القطع.
أقوم الآن بتحديد من كم قطعة في كل مجموعة (مع ملاحظة أن جميع المجموعات تحتوي على نفس العدد من القطع).
 وهكذا تكون مسألة القسمة:
وهكذا تكون مسألة القسمة:
 15 هي عدد القطع جميعها
15 هي عدد القطع جميعها
 3 عدد مجموعات التي نريد التوزيع عليها.
3 عدد مجموعات التي نريد التوزيع عليها.
 إشارة القسمة
إشارة القسمة
 5 هو الناتج والذي يمثل عدد القطع في كل مجموعة.
5 هو الناتج والذي يمثل عدد القطع في كل مجموعة.

أَتَحَدَّثُ: كَيْفَ أُقَسِّمُ 12 قِطْعَةَ عَدٍّ إِلى 4 مَجْموعاتٍ مُتَساوِيَةٍ؟
أُكَوِّنُ مَجْموعاتٍ ثُلاثِيَّةً مِنَ قِطَعِ الْعَدِّ، ثُمَّ أَعُدُّ الْمَجْموعاتِ النّاتِجَةَ.
أُلاحِظُ أَنَّ عَدَدَ الْمَجْموعاتِ يُساوي 4
يتبين أن هناك مجموعات ، وهذه المجموعات متساوية مما يعني أن تحوي نفس العدد من القطع (3 قطع.)
مثال إضافي للتوضيح:
الْقِسْمَةُ كَمَجْموعاتٍ مُتَساوِيَةٍ
إِذا قَسَّمْتُ 20 كرة إِلى مَجْموعاتٍ في كُلٍّ مِنْها 4 كرات، فَما عَدَدُ الْمَجْموعاتِ؟
أُكَوِّنُ مَجْموعاتٍ رباعية مِنَ الكرات، ثُمَّ أَعُدُّ الْمَجْموعاتِ النّاتِجَةَ:.
أُلاحِظُ أَنَّ عَدَدَ الْمَجْموعاتِ يُساوي 5
يتبين أن هناك مجموعات ، وهذه المجموعات متساوية مما يعني أنها تحوي نفس العدد من الكرات(4 كرات.)
أقوم بعد المجموعات المتكونة لديّ، أجد أنها 5 مجموعات.
وهكذا تكون مسألة القسمة:
20 هي عدد الكرات جميعها
4 عدد الكرات في كل مجموعة
إشارة القسمة
5 هو الناتج (المطلوب) والذي يمثل عدد المجموعات المتكونة
مثال إضافي للتوضيح:
لْقِسْمَةُ كَمُشارَكَةٍ بِالتَّساوي
•إِذا قَسَّمْتُ 20 قلم إِلى 4 مَجْموعاتٍ مُتَساوِيَةٍ، فَكَمْ قلم في كُلِّ مَجْموعَةٍ؟
أُوَزِّعُ الأقلام (كل مرة أوزع قلم واحد على الترتيب) حَتىّ تَنتْهَيَ الأقلام جميعها ، ثُمَّ أَجِدُ عَدَدَ الأقلام في الْمَجْموعَةِ كُلِّها.
أُلاحِظُ أَنَّ عَدَدَ الأقلام في كُلِّ مَجْموعَةٍ يُساوي 5
في هذه المسألة لأعرف عدد الأقلام التي تحويها كل مجموعة من المجموعات الأربعة
أقوم بالتوزيع قلم في كل مرة على كل مجموعة، إلى أن ينتهي عد جميع الأقلام.
أقوم الآن بتحديد من كم قلم في كل مجموعة (مع ملاحظة أن جميع المجموعات تحتوي على نفس العدد من الأقلام).
وهكذا تكون مسألة القسمة:
20 هي عدد الأقلام جميعها
4 عدد مجموعات التي نريد التوزيع عليها.
إشارة القسمة
5 هو الناتج والذي يمثل عدد الأقلام في كل مجموعة.