رياضيات فصل ثاني

مُنصِّفاتٌ في المُثلَّثِ

أولًا : المُنصِّفُ العموديُّ

المُنصِّفُ العموديُّ لقطعةٍ مستقيمةٍ هوَ مستقيمٌ عموديٌّ على القطعةِ المستقيمةِ عندَ نقطةِ منتصفِها.

 

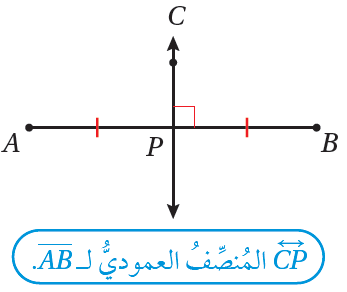
نظريتانِ (المُنصِّفُ العموديُّ)

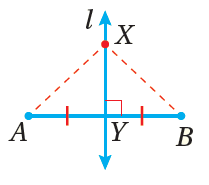
1 ـ نظريةُ المُنصِّفِ العموديِّ : كلُّ نقطةٍ على المُنصِّفِ العموديِّ لقطعةٍ مستقيمةٍ تكونُ على بُعْدينِ متساويينِ منْ طرفيِ القطعةِ المستقيمةِ.  مثال : إذا كانَ  Ɩ مُنصِّفًا عموديًّا لـ $\overline{AB}$ ، فإنَّ $AX = BX$ ، لأيِّ نقطةٍ x على Ɩ
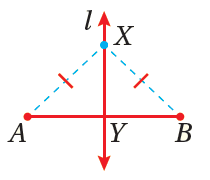
2 ـ · عكسُ نظريةِ المُنصِّفِ العموديِّ :  كلُّ نقطةٍ على بُعْدينِ متساويينِ منْ طرفيْ قطعةٍ مستقيمةٍ تقعُ على المُنصِّفِ العموديِّ لتلكَ القطعةِ. مثال : إذا كانَ $AX = BX$ ، و Ɩ مُنصِّفًا عموديًّا لـ $\overline{AB}$ ، فإنَّ x تقعُ على Ɩ

 

---

ثانيًا : المُنصِّفاتُ العموديةُ للمُثلَّثِ، ومركزُ الدائرةِ الخارجيةِ

إذا تلاقَتْ ثلاثةُ مستقيماتٍ أوْ أكثرُ في نقطةٍ مُشترَكةٍ، فإنَّ هذهِ المستقيماتِ تُسمّى مستقيماتٍ مُتلاقِيةً، وتُسمّى النقطةُ التي تلتقي فيها المستقيماتُ نقطةَ التلاقي.

•• بما أنَّ للمُثلَّثِ ثلاثةَ أضلاعٍ، فإنَّ لهُ ثلاثةَ مُنصِّفاتٍ عموديةٍ تلتقي في نقطةٍ واحدةٍ كما تُبيِّنُ النظريةُ الآتيةُ.

نظريةٌ (المُنصِّفاتُ العموديةُ للمُثلَّثِ)

تلتقي المُنصِّفاتُ العموديةُ لأضلاعِ مُثلَّثٍ في نقطةٍ لها البُعْدُ نفسُهُ عنْ كلٍّ منْ رؤوسِ المُثلَّثِ. مثالٌ : إذا كانَتْ $\overline{PJ} , \overline{PL} , \overline{PK}$ هيَ المُنصِّفاتِ العموديةَ لـ $△ABC$ ، وكانَتِ النقطةُ P هيَ نقطةَ تلاقيها ، فإنَّ $PA = PB = PC$

 

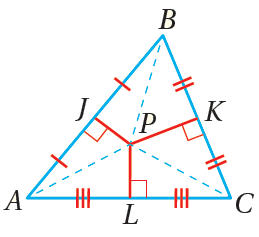•• نقطةُ تلاقي المُنصِّفاتِ العموديةِ لأضلاعِ مُثلَّثٍ ما هيَ مركزُ الدائرةِ الخارجيةِ للمُثلَّثِ ؛ وهيَ دائرةٌ تمرُّ برؤوسِ المُثلَّثِ جميعِها ؛ إذْ إنَّ نقطةَ تلاقي المُنصِّفاتِ العموديةِ لأضلاعِ مُثلَّثٍ ما تبعدُ المسافةَ نفسَها عنْ كلٍّ منْ رؤوسِهِ؛ لذا فهيَ مركزٌ للدائرةِ الخارجيةِ.

---

ثالثًا : مُنصِّفُ الزاويةِ  

نظريتانِ (مُنصِّفُ الزاويةِ)

1) نظريةُ مُنصِّفِ الزاويةِ : كلُّ نقطةٍ على مُنصِّفِ الزاويةِ تكونُ على بُعْدينِ متساويينِ منْ ضلعيْها. مثال : إذا كانَ $PC$ مُنصِّفًا لـ $\angle APB$ ، وكانَ $CA \perp PA , CB \perp PB$، فإنَّ $CA = CB$
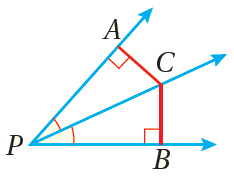2) عكسُ نظريةِ مُنصِّفِ الزاويةِ : إذا وقعَتْ نقطةٌ داخلَ زاويةٍ، وكانَتْ على بُعْدينِ متساويينِ منْ ضلعيْها، فإنَّها تقعُ على مُنصِّفِ الزاويةِ. مثال : إذا كانَ $CA = CB , CA \perp PA , CB \perp PB$ ، فإنَّ $PC$ مُنصِّفٌ لـ $\angle APB$

 

---

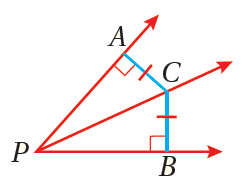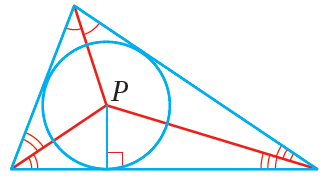
رابعًا : مُنصِّفاتُ زوايا المُثلَّثِ ، ومركزُ الدائرةِ الداخليةِ للمُثلَّثِ

بما أنَّ للمُثلَّثِ ثلاثَ زوايا، فإنَّ لهُ ثلاثةَ مُنصِّفاتٍ للزوايا تلتقي في نقطةٍ واحدةٍ كما تُبيِّنُ النظريةُ الآتيةُ.

نظريةٌ (مُنصِّفاتُ زوايا المُثلَّثِ)

تلتقي مُنصِّفاتُ زوايا المُثلَّثِ في نقطةٍ لها البُعْدُ نفسُهُ عنْ كلٍّ منْ أضلاعِ المُثلَّثِ. مثال : إذا كانَتْ $\overline{PX} , \overline{PY}, \overline{PZ}$ هيَ مُنصِّفاتِ زوايا $△XYZ$، وكانَتِ النقطةُ $P$ هيَ نقطةَ تلاقيها، فإنَّ $PM = PN = PO$

 

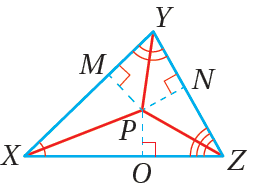•• نقطةُ تلاقي مُنصِّفاتِ زوايا المُثلَّثِ هيَ مركزُ الدائرةِ الداخليةِ للمُثلَّثِ وهيَ دائرةٌ تمسُّ أضلاعَ المُثلَّثِ جميعَها ؛ ذلكَ أنَّ نقطةَ تلاقي مُنصِّفاتِ زوايا المُثلَّثِ تبعدُ المسافةَ نفسَها عنْ كلٍّ منْ أضلاعِهِ ؛ ما يعني أنَّها مركزُ الدائرةِ الداخليةِ.