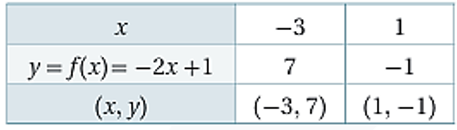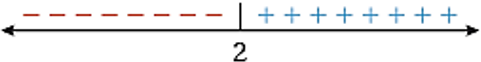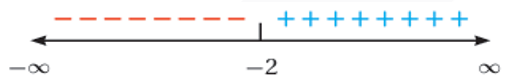• فكرة الدرس :
- تعرف الاقتران المتشعب واقتران القيمة المطلقة
- التمثيل البياني لهما وتحديد مجال كل منهما ومداه .
• الاقتران المتشعب: وهو الاقتران المعرف بقواعد مختلفة عند أجزاء مختلفة في مجاله .
والاقتران المتشعب ، هو اقتران يدمج بين قاعدتي اقترانين أو أكثر .
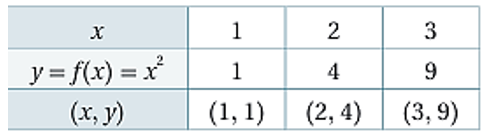
- مثال (1): اذا كان: ، أجب عن الأسئلة الآتية :
| 1) حدد مجال f(x) | 2) جد قيمة f(-2) |
| 3) جد قيمة f(0) | 4) جد قيمة f(2) |
| 5) مثل الأقتران f(x) بيانياً ، ثم حدد مداه |
الإجابة:
| 1) المجال هو الفترة | 2) |
| 3) | 4) |
|
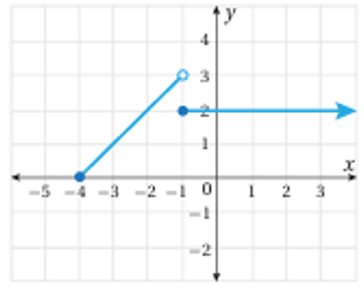
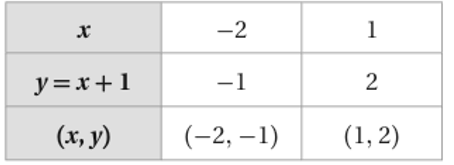
5) اولاً: نجد قيمة الاقتران الخطي: عند طرفي مجاله، أي عندما ، وعندما باستعمال جدول كما يلي:
ثانياً: امثل عندما هو اقتران ثابت، لذا يمثل بشعاع أفقي عند النقطة بدائرة مغلقة لوجود مساواة في رمز المتباينة . |
- من التمثيل البياني للاقتران ، أن مداه هو:
|
- مثال (2): اذا كان: ، أجب عن الأسئلة الآتية:
| 1) حدد مجال f(x) | 2) جد قيمة f(-2) | 3) جد قيمة f(1) |
| 4) مثل الأقتران f(x) بيانياً ، ثم حدد مداه. | ||
الإجابة:
| 1) المجال هو الفترة: | 2) | 3) |
|
4) اولاً : امثل عندما عندما وعندما كما في الجدول الآتي:
ثانيا: أمثل عندما وهو جزء من منحنى قطى مكافىء مفتوح الى الأعلى - أنشىء جدول قيم ، لارسم الجزء من منحنى القطع المكافىء الذي يقع يمين العدد 1
|
- مدى الاقتران هو: |
 |
تدريب: إذا كان:
a) أجد مجال f(x).
b) أجد قيمة كل من f(5) ، و f(2) , و f(0).
c) أمثل الاقتران f(x) بيانيًا، وأحدد مداه.
• كيف أجد قاعدة الاقتران المتشعب ، اذا أعطيت تمثيله البياني ؟
سنتعلم ذلك من خلال الأمثلة الآتية :
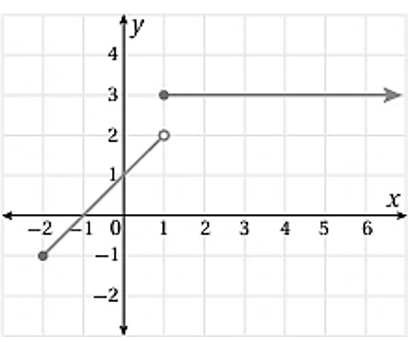
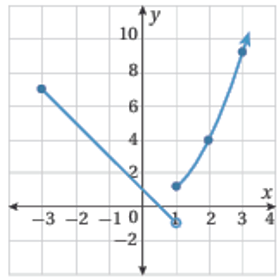
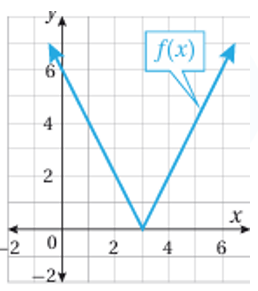
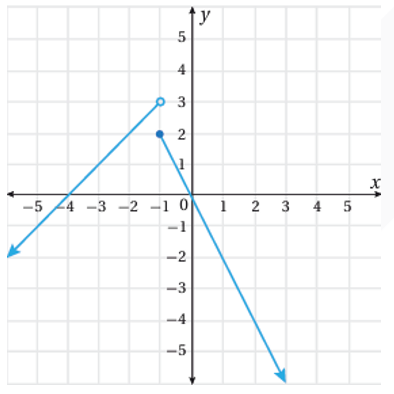
• مثال (3) : أكتب قاعدة الاقتران المتشعب الممثل بيانياً في الشكل المجاور .
|
اولاً : أكتب قاعدة الاقتران الذي يمثل الجزء الايسر من التمثيل البياني وهو شعاع يمر بالنقطتين: وميله :
ومن ثم ، فأن معادلة الشعاع بصيغة الميل والنقطة هي: ويمكن كتابتها في صورة: اما وجود دائرة مفتوحة عند النقطة فيعني ان هذه القاعدة تقابل الفترة ثانياً : أكتب قاعدة الاقتران الذي يمثل الجزء الايمن من التمثيل البياني وهو شعاع يمر بالنقطتين: وميله: ومن ثم ، فإن معادلة الشعاع يقطع المحور y عند الصفر b=0 ، فأن معادلته بصيغة الميل والمقطع هي: أو
|
 |
|
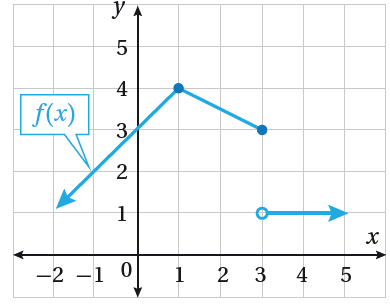
تدريب: أكتبُ قاعدة الاقتران f(x) الممثل بيانيُا في الشكل المجاور. الإجابة: |
 |
ويمكن نمذجة كثير من المواقف الحياتية باستعمال الاقترانات المتشعبة .
• اقتران القيمة المطلقة: هو اقتران يحتوي على قيمة مطلقة لمقدار جبري.
مثلا:
 |
• خطوات اعادة تعريف اقتران القيمة المطلقة :
|
- مثال (4): أعد تعريف القيمة المطلقة
الإجابة:
|
|
- مثال (5): أعد تعريف القيمة المطلقة
|
|
- تدريب: أعد تعريف القيمة المطلقة
|
• تمثيل اقتران القيمة المطلقة بيانياً : - يمكن تمثيل اقتران القيمة المطلقة بيانياً باستعمال محور التماثل والرأس. |
- مثال (6): مثل بيانياً كل اقتران ممّا يأتي ، ثم حدد مجاله ومداه :
| 1) | 2) |
| الإجابة: | |
|
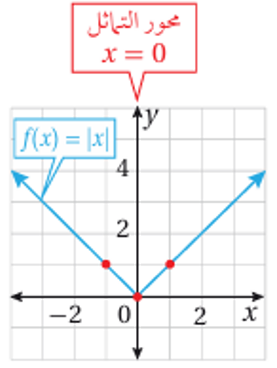
1) اولاً : نجد احداثي رأس الاقتران ، ومعادلة محور التماثل :
اذن ، احداثيا نقطة الرأس ومعادلة محور التماثل (المحور y ) ثانياً : احدد قيمتين للمتغير x حول محور التماثل ، ثم أجد صورتيهما . بما أن محور التماثل x=0 أختار قيمة للمتغير x اكبر من 0 وقيمة أخرى اقل من 0 ثم اجد صورتيهما في الاقتران .
ثالثاً : نمثل النقطتين والرأس بيانياً: نلاحظ من التمثيل البياني أن المجال هو مجموعة الأعداد الحقيقية ، وان المدى
|
|
|
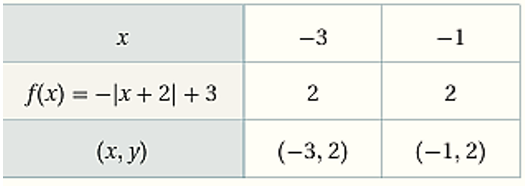
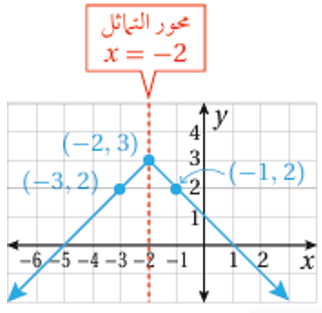
2) احداثيا نقطة الرأس (2,3) ، ومعادلة محور التماثل x=-2
- نمثل النقطتين والرأس بيانياً
|
|
- تدريب : مثل بيانياً الاقتران الأتي، وحدد مجاله ومداه:
يمكن ايجاد قاعدة اقتران القيمة المطلقة لمقدار خطي ، اذا أعطي تمثيله البياني .
|
نجد ميل المعادلة الخطية داخل رمز القيمة المطلقة
- نجد قيمة a
|
|
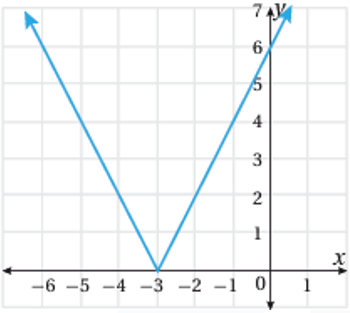
تدريب: أكتب قاعدة اقتران القيمة المطلقة f(x) الممثل بيانياً في الشكل المجاور .
ورقة عمل:
1) إذا كان: فإنّ قيمة: هي:
2) إذا كان: فإن قيمة: هي:
3) إذا كان: فإنّ قيمة: هي:
4) مجال الاقتران الذي يظهر تمثيله البياني في الشكل المجاور هو :