رياضيات 7 فصل ثاني

مفهوم أساسي: 

علاقةُ التغير العكسيِّ (Inverse variation): هيَ علاقةٌ بينَ كمّيتَينِ بحيثُ تؤدي زيادةُ الكميةِ الأولى إلى نقصانِ الكمّيةِ الثانيةِ 

 إذا وُجدَتْ علاقةُ تغير عكسيٍّ بينَ المتغيّرَينِ y وَ x فإنَّ ناتجَ ضربِهِما يساوي ثابتًا هو K.

  x × y = k حيثُ k ≠ 0

   تمثل $\mathrm{y}=\frac{\mathrm{k}}{\mathrm{x}}$ معادلةَ التغير العكسيِّ

 

x	5	10	25	50
y	20	10	4	??

: y وَ x مثال 1: يمثّلُ الجدولُ المجاورُ علاقةً بينَ المتغيّرَين

1) أبيّنُ أنَّ العلاقة بين x وy تمثل تغيرًا عكسيًّا، ثمَّ أَجِدُ ثابتَ التغير k

 أَجِدُ x × y للقِيَمِ المتناظِرةِ جميعِها:

x × y $\to$ 5 × 20 =100, 10 ×10 =100, 25 × 4 = 100

.k = وثابت التغير 100  y وَ x متساوٍ للأزواجِ المرتَّبةِ جميعِها، إذنْ، توجَدُ علاقةُ تغير عكسيٍّ بينَ المتغيّرَينِ x×y ألاحظُ أنَّ ناتجَ

2) أكتبُ معادلةَ التغير العكسيِّ، ثم أَجِدُ القيمةَ المجهولةَ في الجدولِ السابقِ.

$\mathrm{y}=\frac{100}{\mathrm{x}}$                    أكتبُ معادلةَ التغير العكسيِّ

$\mathrm{y}=\frac{100}{50}$                    أُعوّضُ x=50 في المعادلةِ 

y=2                            أَجِدُ الناتجَ  

 

مثال 2: منَ الحياةِ يمثّلُ الجدولُ المجاورُ العلاقةَ بينَ معدَّلِ السرعةِ والزمنِ اللازمِ لقطعِ المسافةِ بينَ عمّانَ والطفيلةِ الّتي تساوي $180 km$ :

الزمن h	معدل السرعة  Km/h
2	90
2.5	72
3	60
4	45

1) أبيّنُ أنَّ العلاقة بين معدَّلَ السرعةِ والزمنَ تمثل تغيرًا عكسيًّا ثمَّ أَجِدُ ثابتَ التغير k 

معدل السرعة $\times$الزمن  $\to$ $2\times 90 = 180, 2.5 \times 72 = 180, 3 \times 60 = 180, 4 \times 45 = 180$ 

.k = ألاحظُ أنَّ ناتجَ الضربِ متساوٍ للقِيَمِ المتناظِرةِ جميعِها؛ إذنْ، العلاقة بين معدَّلُ السرعةِ وَالزمنُ علاقة تغير عكسيّ، وثابتُ التغير 180

2) أكتبُ معادلةَ العلاقةِ.

$\mathrm{y}=\frac{180}{\mathrm{x}}$

 

يُمكنُنا إيجادُ ثابتِ التغير لعلاقةِ تغير عكسيٍّ ممثَّلةٍ بيانيًّا، وذلكَ بتحديدِ زوجٍ مرتَّبٍ على التمثيلِ البيانيِّ، وتعويضِ قيمةِ y وَ x  في معادلةِ التغير العكسيِّ. 

 

مثال 3 : يبيّنُ الشكلُ المجاورُ تغيرًا عكسيًا بينَ المتغيّرَينِ  y وَ x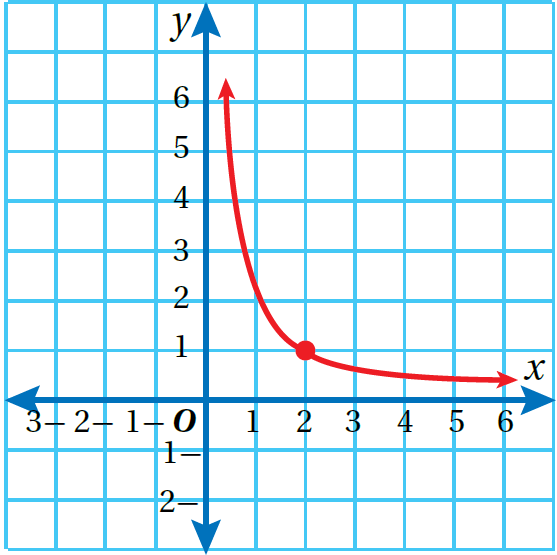 

1)أَجِدُ ثابتَ التغير  k

أختارُ زوجًا مرتَّبًا على التمثيلِ البيانيِّ للعلاقةِ، مثلَ (2,1) وأعوّضُهُ في معادلةِ التغير العكسيِّ.

$\text{y=}\frac{\mathrm{k}}{\mathrm{x}}$                          أكتبُ معادلةَ التغير العكسيِّ

$1=\frac{\mathrm{k}}{2}$                        أُعوّضُ x=2 , y=1 في المعادلةِ  

 k =  2                         بالضربِ التبادليِّ أَجِدُ الناتجَ

2)أكتبُ معادلةَ التغير العكسيِّ:

$\mathrm{y}=\frac{2}{\mathrm{x}}$

 

مثال 4: منَ الحياةِ محيطاتٌ: يبيّنُ الجدولُ المجاورُ العلاقةَ بينَ عُمقِ الماءِ وَدرجاتِ الحرارةِ في المحيطِ الأطلسيِّ:

	العمق Ft		الحرارة $f^{°}$
500	28
1000	14
2000	7

1) أحددُ ما إذا كانَتِ العلاقةُ تمثّلُ علاقةَ تغير طرديٍّ أَمْ عكسيٍّ.

ألاحظُ مِنَ الجدولِ أنَّهُ كلّما ازدادَ العُمقُ انخفضَتْ درجَةُ الحرارةِ؛ لذا، لا يُمكنُ أنْ تمثِّلَ العلاقةُ تغيرًا طرديًّا

أختبرُ ما إذا كانَتِ العلاقةُ تمثّلُ تغيرًا عكسيًّا:

$\mathrm{العمقُ} \times \mathrm{الحرارةِ} \mathrm{درجة} \to$  500 × 28 = 14000, 1000 × 14 = 14000,  2000 × 7 = 14000

ألاحظُ أنَّ ناتجَ الضربِ متساوٍ للقِيَمِ المتناظِرةِ جميعِها، إذنْ، تمثل العلاقة بين درجةُ الحرارةِ وَعُمقُ الماءِ تغيرًا عكسيًّا، وثابتُ التغير k=14000

2) أكتبُ معادلةَ التغير العكسيِّ.

$\mathrm{y}=\frac{14000}{\mathrm{x}}$

3) أمثّلُ علاقةَ التغير بيانيًّا.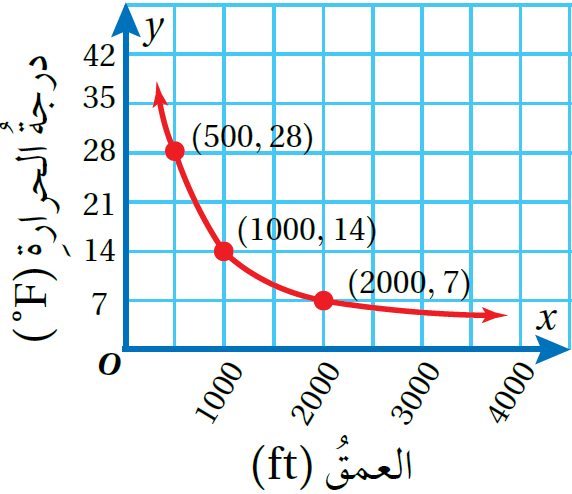
أمثلُ الأزواجَ المرتبةَ في الجدولِ في المستوى الإحداثيِّ، ثمَّ أرسمُ خطًّا منحنيًا يمرُّ بها جميعًا. 

4)أَجِدُ درجةَ الحرارةِ على عُمقِ 7000ft 

$\mathrm{y}=\frac{14000}{\mathrm{x}}$                 أكتبُ معادلةَ التغير العكسيِّ

$\mathrm{y}=\frac{14000}{7000}$                 أُعوّضُ x=7000 في المعادلةِ 

y=2                               أَجِدُ الناتجَ

درجةَ الحرارةِ على عُمقِ 7000ft تساوي $2^{°}\mathrm{f}$