الجذور التربيعية

أتعلم : 

1- تسمى الأعداد 1 ، 4 ، 9، 16 ، 25 مربعات كاملة : لأنها ناتجة عن مربعات أعداد صحيحة .

2- الجذر التربيعي : هو أحد عاملين متساويين لعدد ما .
3- لأي عدد موجب جذران تربيعيان  ، أحدهما موجب والآخر سالب 
4- يسمى الرمز $\sqrt[]{}$ رمز الجذر ، ويستعمل للدلالة على الجذر التربيعي الموجب  

5- يسمى العدد أسفل الجذر : المجذور 

6- يُقرأ الرمز ± موجبًا أَوْ سالبًا، ويدلُّ على كِلا الجذرين التربيعيَّين للعددِ الموجب.

---

توضيح :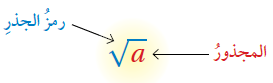 

 

 

 

 

 

 

 

---

مثال 1 : أجدُ كلًّ مِنَ الجذورِ التربيعيةِ الآتيةِ :

 1)  $\sqrt[]{36}$   = +6

نجد الجذر التربيعي الموجب للعدد 36 (أحد العاملين المتساويين اللذين حاصل ضربهما 36)

2) $\mathbf{\pm }\sqrt[]{\mathbf{1}\mathbf{.}\mathbf{69}}$ = $\mathbf{\pm }\mathbf{ }\mathbf{1}\mathbf{.}\mathbf{3}$

نجد الجذرين التربيعين  للعدد 1.69(أحد العاملين المتساويين اللذين حاصل ضربهما 1.69)

3)$\mathbf{-}\sqrt[]{\frac{\mathbf{25}}{\mathbf{64}}}$ = $\mathbf{-}\frac{\mathbf{5}}{\mathbf{8}}$

نجد الجذر التربيعي السالب للعدد 25, والعدد 64 (أحد العاملين المتساويين اللذين حاصل ضربهما 25 , 64)

---

ملاحظات هامة :

1)  يمكن تسهيل إيجاد الجذر التربيعي لعدد عشري (كما في الفرع الثاني) ، وذلك بتحويل العدد إلى كسر ، ثم إيجاد الجذر للبسط والمقام 

فمثلاً : $\sqrt[]{\mathbf{1}\mathbf{.}\mathbf{69}}\mathbf{ }\mathbf{=}\sqrt[]{\frac{\mathbf{169}}{\mathbf{100}}}\mathbf{ }\mathbf{=}\frac{\mathbf{13}}{\mathbf{10}}\mathbf{ }\mathbf{=}\mathbf{1}\mathbf{.}\mathbf{3}$  

2) يمكن استعمال تعريف الجذرِ التربيعي لعددٍ موجب في حلّ معادلات تتضمن متغيرات مربعة، فإذا كانَ  :
${\mathit{n}}^{\mathbf{2}}\mathbf{=}\mathbf{ }\mathit{c}\mathbf{\Rightarrow }\mathit{n}\mathbf{=}\mathbf{ }\mathbf{\pm }\sqrt[]{\mathbf{c}}$

3) مربعات كاملة هامة  :

العدد :	مربع العدد
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144
13	169
14	196
15	225
16	256
17	289
18	324
19	361
20	400

 

4) قيمة العدد السالب تحت الجذر التربيعي : غير معرّفة

---

مثال 2 : أحل كلّ مِن المعادلات الآتية ، وأتحقق مِن صحةِ الحل :

1) ${\mathit{x}}^{\mathbf{2}}\mathbf{=}\mathbf{ }\mathbf{144}\mathbf{\Rightarrow }x=\pm \sqrt[]{144}\Rightarrow x=\pm 12$

 

.  ${\mathit{x}}^{\mathbf{2}}$ يمكن التحقق من صحة الحل بتعويض 12+, 12- عوضاً عن 

 

2) $t^{\mathbf{2}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{36}}\mathbf{\Rightarrow }t=\pm \sqrt[]{\frac{1}{36}}\Rightarrow t =\pm \frac{1}{6}$

 

يمكن التحقق من صحة الحل بتعويض $-\frac{1}{6}$, $+\frac{1}{6}$-  عوضاً عن ${\mathit{t}}^{\mathbf{2}}$ .

 

---

 

مثال 3: منَ الحياةِ :
أهرامٌ: هرمُ الشمسِ في المكسيكِ ثالثُ أكبرِ هرمٍ في العالمِ، قاعدتُهُ مربعةُ الشكلِ مساحتها $50625 m^2$ ، جد طول ضلع قاعدته .

 

الحل :  1) نكتب قانون مساحة المربع ثم نعوض :  $A= s^2\Rightarrow x^2=50625$

2) نبحث عن عاملين متساويين للعدد 50625 ، وذلك بتحليله إلى العوامل الأولية على النحو التالي :

 $50625 = 5\times 5\times 5 \times 5 \times 3 \times 3 \times 3 \times 3$

$= (5 \times 5 \times 3 \times 3) (5\times 5\times 3\times 3) = 225 \times 225$

3)  الجذر التربيعي للعدد 50625 هو أحد العوامل التي حصلنا عليها:

$x^2=50625\Rightarrow x = \pm \sqrt[]{50625}\Rightarrow \mathit{x}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{\pm }\mathbf{ }\mathbf{225}$
 

ولأن الطول لا يمكن ان يكون سالباً ، نهمل الإجابة السالبة وعليه فإن طول قاعدة الهرم تساوي 225m.

---