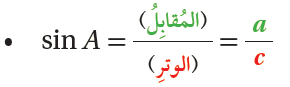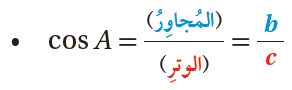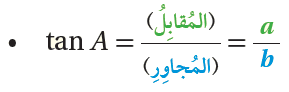رياضيات 9 فصل ثاني

النسبُ المُثلَّثيةُ

Trigonometric Ratios

فكرةُ الدرسِ: تعرُّفُ جيبِ الزاويةِ الحادة ، وجيبِ تمامِها، وظلِّها، بوصفِها نسبًا بينَ أضلاعِ مُثلَّثٍ قائمِ الزاويةِ.

 

أولًا : النسبُ المُثلَّثيةُ

النسبةُ المُثلَّثيةُ (trigonometric ratio): هيَ نسبةٌ بينَ طوليْ ضلعينِ منْ أضلاعِ المُثلَّثِ قائمِ الزاويةِ.

نظريةٌ (النسبُ المُثلَّثيةُ)

إذا كانَ ΔABC قائمَ الزاويةِ، وكانَتِ $\angle A$  زاويةً حادَّةً فيهِ، فإنَّ نسبَ المُثلَّثِ التي هيَ أكثرُ شيوعًا تُعرَفُ بدلالةِ الوترِ، والضلعِ المُقابِلِ، والضلعِ المُجاوِرِ كما يأتي : الجيبُ  (sine)   جيبُ التمامِ (cosine) الظلُّ (tangent)

 

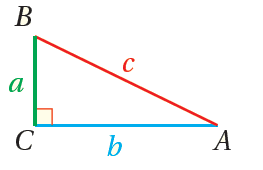•• رموزٌ رياضيةٌ: تشيرُ الأحرفُ الكبيرةُ (A, B, C)  إلى رؤوسِ المُثلَّثِ، في حينِ تشيرُ الأحرفُ الصغيرةُ (a, b, c) إلى الأطوالِ المُقابِلةِ لتلكَ الرؤوسِ.
فمثلًا ، يشارُ إلى طولِ الضلعِ المُقابِلِ للزاويةِ A بالحرفِ a، وهكذا.

 

مثال 1 : 

أجدُ قِيَمَ النسبِ المُثلَّثيةِ الثلاثِ للزاويةِ G في المُثلَّثِ المُجاوِرِ.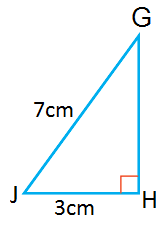

الحل : 

الخطوةُ 1: أستعملُ نظريةَ فيثاغورس لإيجادِ GH

${\left(JG\right)}^2={\left(HG\right)}^2+{\left(JH\right)}^2$	نظريةُ فيثاغورس
${\left(7\right)}^2={\left(HG\right)}^2+{\left(3\right)}^2$	بتعويض $JG=7, JH=3$
$49={\left(HG\right)}^2+9$	بالتبسيطِ
${\left(HG\right)}^2=40$	بطرح 9 من طرفي المعادلة
$HG=\pm \sqrt{40}$	بأخذِ الجذرِ التربيعيِّ لطرفيِ المعادلةِ

بما أنَّ الطولَ لا يُمكِنُ أنْ يكونَ سالبًا، فإنَّ $HG=\sqrt{40}$

الخطوةُ 2 : أجدُ النسبَ المُثلَّثيةَ الثلاثَ.

$\tan G=\frac{JH}{HG}=\frac{3}{\sqrt{40}}$

$\cos G=\frac{HG}{JG}=\frac{\sqrt{40}}{7}$

$\sin G=\frac{JH}{JG}=\frac{3}{7}$

---

ثانيًا : النسبُ المُثلَّثيةُ، والآلةُ الحاسبةُ

يُمكِنُ إيجادُ قِيَمِ النسبِ المُثلَّثيةِ لزوايا معلومةٍ باستعمالِ الآلةِ الحاسبةِ.

•• أتعلَّمُ: أضبطُ الآلةَ الحاسبةَ على خيارِ ( DEGREES ) قبلَ استعمالِها.

مثال 2: 

أجدُ قيمةَ كلٍّ ممّا يأتي باستعمالِ الآلةِ الحاسبةِ، مُقرِّبًا إجابتي إلى أقربِ ثلاثِ منازلَ عشريةٍ:

$\mathbf{1}\mathbf{)}\mathbf{ }\sin 40°$

اضغط على مفتاح sin ، ثمَّ أُدخِلُ القيمةَ 40 ، ثمّ اضغط على مفتاح =  ، فتظهر النتيجة :

$sin40°=0.642787609687$                                                                                    
 

بالتقريبِ إلى ثلاثِ منازلَ عشريةٍ، فإنَّ النتيجةَ هيَ: 0.643

إذن:$sin40°\approx 0.643$

---

$\mathbf{2}\mathbf{)} \cos 68°$

اضغط على مفتاح cosine ، ثمَّ أُدخِلُ القيمةَ 68 ، ثمّ اضغط على مفتاح  =  ، فتظهر النتيجة :

$\cos 68°=0.374606593416$                                                                         

بالتقريبِ إلى ثلاثِ منازلَ عشريةٍ، فإنَّ النتيجةَ هيَ : 0.375           

إذن:$\cos 68°\approx 0.375$                                                                                             

---

$\mathbf{3}\mathbf{)} \tan 37°$

اضغط على مفتاح tan ، ثمَّ أُدخِلُ القيمةَ 37، ثمّ اضغط على مفتاح =، فتظهر النتيجة :

$\tan 37°=0.753554050103$                                                                   

بالتقريبِ إلى ثلاثِ منازلَ عشريةٍ، فإنَّ النتيجةَ هيَ: 0.754   

إذن:$\tan 37°\approx 0.754$

---

•• يُمكِنُ استعمالُ الآلةِ الحاسبةِ لإيجادِ أيِّ زاويةٍ حادَّةٍ في المُثلَّثِ قائمِ الزاويةِ إذا عُلِمَتْ إحدى نسبِها، وذلكَ باستعمالِ

معكوسِ النسبةِ المُثلَّثيةِ (inverse trigonometric ratio ).

فإذا عُلِمَ جيبُ الزاويةِ، فإنَّني أستعملُ معكوسَ الجيبِ $\left({\sin }^{-1}\right)$ ، وإذا عُلِمَ جيبُ تمامِ الزاويةِ، فإنَّني أستعملُ معكوسَ جيبِ التمامِ $\left({\cos }^{-1}\right)$، وإذا عُلِمَ

ظلُّ الزاويةِ، فإنَّني أستعملُ معكوسَ الظلّ $\left({\tan }^{-1}\right)$.

•• لغةُ الرياضياتِ: يُقرَأُ معكوسُ الجيبِ : sine inverse ، ويُرمَزُ إليْهِ بالرمزِ $\left({\sin }^{-1}\right)$.     يُقرَأُ معكوسُ جيبِ التمامِ : cosine inverse ، ويُرمَزُ إليْهِ بالرمزِ $\left({\cos }^{-1}\right)$. يُقرَأُ معكوسُ الظلِّ : tan inverse ، ويُرمَزُ إليْهِ بالرمزِ $\left({\tan }^{-1}\right)$.

 

مثال 3 : 

أجدُ قياسَ$\angle A$الحادَّةِ في كلٍّ ممّا يأتي، مُقرِّبًا إجابتي إلى أقربِ منزلةٍ عشريةٍ واحدةٍ:

 $\mathbf{1}\mathbf{)} \sin A=0.6$

$\sin A=0.6$	النسبةُ المعطاةُ
$m\angle A={\sin }^{-1}(0.6)$	معكوسُ الجيبِ

والآنَ أستعملُ الآلةَ الحاسبةَ لإيجادِ ${\sin }^{-1}(0.6)$ كما يأتي :

اضغط على مفتاح SHIFT ، ثمَّ مفتاح sin  ثمّ أُدخِلُ القيمةَ 0.6 ، ثمّ اضغط على مفتاح  =  ، فتظهر النتيجة :

$SHIFT sin(0.6)=36.869897645844$                                                                             

بالتقريبِ إلى أقربِ منزلةٍ عشريةٍ واحدةٍ، فإنَّ النتيجةَ هيَ:$36.9°$

إذنْ: $\angle A\approx 36.9°$

---

$\mathbf{ }\mathbf{2}\mathbf{)} \cos A=\frac{3}{8}$

$\cos A=\frac{3}{8}$	النسبةُ المعطاةُ
$m\angle A=co{s}^{-1}\left(\frac{3}{8}\right)$	معكوسُ جيبِ التمامِ

اضغط على مفتاح  SHIFT ، ثمَّ مفتاح cos ثمّ أُدخِلُ القيمةَ  $\frac{3}{8}$ ، ثمّ اضغط على مفتاح =  ، فتظهر النتيجة :

$SHIFT \cos (3÷8)=67.9756871629578$

بالتقريبِ إلى أقربِ منزلةٍ عشريةٍ واحدةٍ، فإنَّ النتيجةَ هيَ: $68°$

إذنْ: $\angle A\approx 68°$

---

$\mathbf{3}\mathbf{)} \tan A=\frac{14}{9}$

$\tan A=\frac{14}{9}$	النسبةُ المعطاةُ
$m\angle A={\tan }^{-1}\left(\frac{14}{9}\right)$	معكوسُ الظلّ

اضغط على مفتاح  SHIFT ، ثمَّ مفتاح tan  ثمّ أُدخِلُ القيمةَ $\frac{14}{9}$ ، ثمّ اضغط على مفتاح  =  ، فتظهر النتيجة :

$SHIFT \tan (14÷9)=57.2647737278924$

بالتقريبِ إلى أقربِ منزلةٍ عشريةٍ واحدةٍ، فإنَّ النتيجةَ هيَ : $57.3°$

إذنْ : $\angle A\approx 57.3°$

---

ثالثًا : العلاقةُ بينَ الجيبِ وجيبِ التمامِ

نظريةٌ (مُتطابِقةُ فيثاغورس)

في أيِّ مُثلَّثٍ قائمِ الزاويةِ، حيثُ A زاويةٌ حادَّةٌ في المُثلَّثِ، فإنَّ :   $si{n}^{2}A+co{s}^{2}A=1$

 

مثال 4:

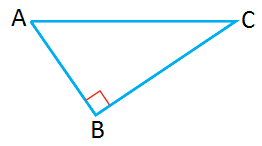في المُثلَّثِ المُجاوِرِ، إذا كانَ $\sin C=0.8$ فأجد $\cos C$

الحل : 

$si{n}^{2}C+co{s}^{2}C=1$	مُتطابِقةُ فيثاغورس
${(0.8)}^2+co{s}^{2}C=1$	بتعويضِ $\sin C=0.8$
$0.64+co{s}^{2}C=1$	بالتربيعِ
$co{s}^{2}C=0.36$	بطرحِ 0.64 من طرفي المعادلة
$cosC=\pm 0.6$	بأخذِ الجذرِ التربيعيِّ للطرفينِ

 

بما أنَّ جيبَ التمامِ للزاويةِ C في المُثلَّثِ قائمِ الزاويةِ ABC هوَ ناتجُ قسمةِ طولِ الضلعِ المُجاوِرِ على الوترِ، وبما أنَّ الأطوالَ لا يُمكِنُ أنْ تكونَ سالبةً، فإنَّ

cos C قيمةٌ موجبةٌ ؛ أيْ $cosC=0.6$

---

 

•• أتعلَّمُ : قيمةُ كلٍّ منَ الجيبِ، وجيبِ التمامِ، والظلِّ موجبةٌ لأيِّ زاويةٍ حادَّةٍ.

رابعًا: الجيبُ وجيبُ التمامِ للزوايا المُتتامَّةِ 

مفهومٌ أساسيٌّ (الجيبُ وجيبُ التمامِ للزوايا المُتتامَّةِ)

إذا كانَ A و B زاويتينِ مُتتامَّتينِ في مُثلَّثٍ قائمِ الزاويةِ، فإنَّ: $\sin A=\cos (90°-A)=\cos B$ $\sin B=\cos (90°-B)=\cos A$ $\cos A=\sin (90°-A)=\sin B$ $\cos B=\sin (90°-B)=\sin A$

 

مثال 5: 

إذا كانَ $\sin 39°=0.6293$ ، فأجد $\cos 51°$ .

الحل: 

$\sin A=\cos (90°-A)$	تعريفُ الجيبِ وجيبِ التمامِ للزوايا المُتتامَّةِ
$\sin 39°=\cos (90°-39)$	بتعويضِ $A=39°$
$\sin 39°=\cos (51°)$	بالتبسيطِ
$\cos (51°)=0.6293$	بتعويضِ $\sin 39°=0.6293$