فيزياء10 فصل أول

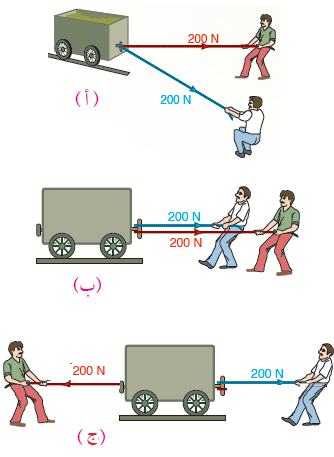
جمع المتجهات:

تعرفنا سابقا أن الكميات الفيزيائية  تكون اما قياسية تحدد بمقدار فقط  ، أو متجهة تحدد

بمقدار واتجاه. وأن عملية   ضرب الكميات المتجه تختلف  عن ضرب  الكميات القياسية .

ولكن  ماذا عن الجمع؟ فمثلا اذا كانت درجة الحرارة اليوم ^º20  ودرجة الحرارة

المتوقعة غدا24^º فهذا يعني أن درجة الحرارة الحرارة  غدا سترتفع 4^ºC ،  لكن هل تختلف 

عملية جمع الكميات المتجهة وطرحها عنها للكميات القياسية؟ 

• عند جمع  وطرح الكميات  المتجهة   يجب مراعاة  الاتجاهات فمثلا بالشكل   أ  

لو قلنا أن مجموع قوتي الرجلين المؤثرةلسحب العربة هو مجموع جبري 

أي (200+200=400N)  تكون  الاجابة غير صحيحة لان القوتين   ليستا بنفس الاتجاه

كما في الشكل ب  حيث قوتا الرجلين بنفس الاتجاه حيث   مجموع القوتين ( 400N).

وفي الشكل ج، قوتا الرجلين  متعاكستين وجموع القوتين (0 = 200-200  )

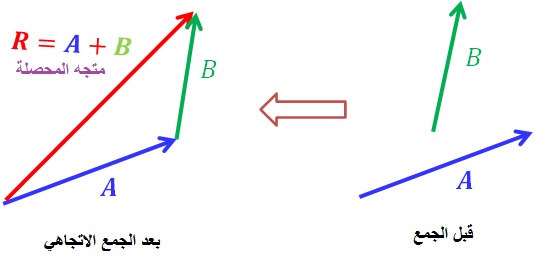
• نستنتج ما سبق ان ناتج جمع متجهين مثل   (A,B)  هو متجه جديد (A+B) 

يختلف مقداره واتجاهه   عن كل من المتجهين.

• بشكل عام يسمى المتجه الناتج من الجمع المتجهي  لعدة متجهات ( A , B . C )

متجه المحصلة R

حيث (R=A+B+C) على أن تكون المتجهات من النوع نفسه  فمثلا ناتج جمع 

(محصلة) متجهات سرعة  هو متجه سرعة  وينطبق ذلك على المتجهات جميعها.

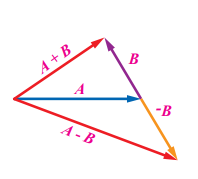
طرح المتجهات:

 عملية طرح المتجهات تعني عملية جمع معكوس  المتجه المراد طرحه 

أي أن طرح المتجه يكافيء جمع سالب ذلك المتجه. فمثلا  عند طرح المتجه B

من المتجه A يعني أن نجمع المتجه A مع معكوس المتجهB  أي (-B)  .

$\mathit{A}\mathbf{-}\mathit{B}\mathbf{=}\mathbf{ }\mathit{A}\mathbf{+}\mathbf{(}\mathbf{-}\mathit{B}\mathbf{)}$

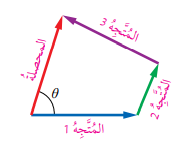
محصلة متجهات عدة:

أ- الطريقة البيانية

 هي طريقة تتلخص في تمثيل المتجهات المراد جمعها بأسهم وتركيب

 تلك الاسهم بطريقة  متوازي الأضلاع  أو المضلع  ( الذيل  على الرأس).

 طريقة المضلع ( الذيل على الرأس): 

 لايجاد محصلة عدة متجهات بيانيا ، نتبع الخطوات التالية:

 1- اختيار مقياس رسم مناسب ، ورسم أسهم تمثل المتجهات المراد

     جمعها.

2- رسم المتجه الـأول   ثم رسم المتجه الثاني بحيث  يقع ذيل  المتجه الثاني

  عند رأس المتجه الأول  مع  المحافطة على  المقدار والاتجاها ، وهكذا الحال

 لبقية المتجهاتحتى أخر متجه.

3- رسم سهم من ذيل المتجه الأول الى رأس المتجه الأخير  ليمثل طوله

 مقدار المحصلة ، واتجاهه ( من الذيل للرأس )  اتجاه المحصلة .   

كما في الشكلين ( أ ) و (ب) في الطريقة البيانية يكون متجه المحصلة

 لعدة متجهات هو  متجه ذيله عند ذيل  المتجه الأول ورأسه عند رأس

 المتجه الأخير كما في الشكلين  أ و ب.

والمشهد الحركي المقابل. ( المتجه المحصل :(  $\overrightarrow{v} + \overrightarrow{w}$ )

   الشكل أ: محصلة  متجهين ( A ,  B )

   الشكل ب: محصلة ثلاثة  كمتجهات

             محصلة لأربعة متجهات

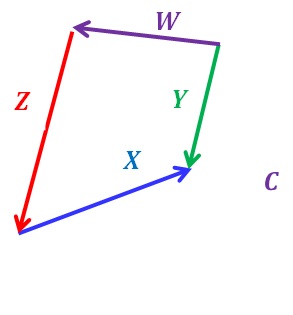
 فكر 1: 

  يمثل الشكل  المجاور  مضلع لتمثيل أربعة متجهات بالطريقة

 البيانية ( ألمضلع)  أي المتجهات الواردة في الشكل يمثل متجه

المحصل؟ 

                  اضغط هناالمتجه Y، لأن ذيله مع ذيله مه ذيل وتجه ورأسه مع رأس متجه

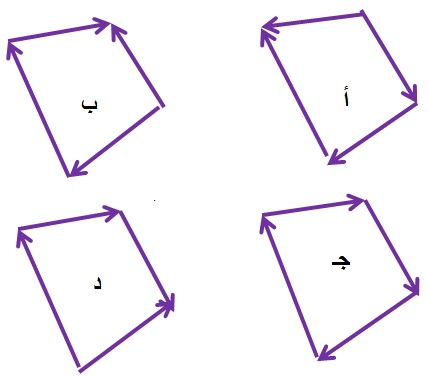
فكر 2: 

    أي الأشكال  المقابلة  يكون لها  المتجه  المحصل يساوي صفر؟

        بعد أن تفكر:اضغط هناجـ ( مضلع مغلق، جميعها ذيل مع رأس

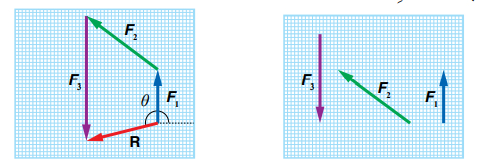
  مثال: تُؤثِّرُ ثلاثُ قوى في جسمٍ: القُوَّةُ الأولى F₁ مقدارُها 30N

في اتجاهِ الشمالِ، والقُوَّةُ الثانيةُ F₂ مقدارُها 50 N في  اتجاهٍ

 يَصنعُ زاويةً مقدارُها 37^o شمالَ الغربِ، والقُوَّةُ الثالثةُ F₃

مقدارُها 70N في اتجاهِ الجنوبِ. أَجِدُ مقدارَ  محصلةِ القوى 

 المؤثِّرةِ في الجسمِ واتجاهَها بيانيًّا.

أ- نختار مقياس رسم مناسب  مثلا (1cm:10N)  ,ونرسم ثلاث

 متجهات  ليكون طول كل متجه :$F_1:3cm$ ،    $F_2: 5cm, F_3:7cm$

ب- نرسم متجه القوة الأول F_{1 ،} ثم نرسم سهم متجه القوة الثاني F₂

    بحيث يقع ذيله عند رأس  سهم F₁  ثم نرسم سهم متجه القوة 

   الثالث F₃ بحيث يقع ذيله عند  راس المتجه الثاني .

ج- نرسم  المحصلة من ذيل المتجه الاخير الى رأس المتجه الأول 

د- نقيس بالمسطرة  طول متجه المحصلة R وبحسب مقياس

 الرسم  تكون المحصلة $R=4.1\times 10=41 m$، ونقيس بالمنقلة الزاوية

  بين متجه المحصلة ومحور x+ بعكس دوران عقارب الساعة $\theta = {194}^{\circ }$

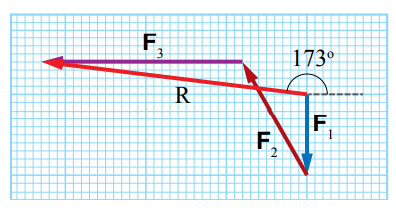
  تمرين  صفحة 26:

شحنة كهربائية  تؤثر فيها ثلاث قوى على النحو الآتي:

200N في اتجاه الجنوب، 300N في اتجاه يصنع زاوية

مقدارها  (53^o ) شمال الغرب ، 500N  في اتجاه الغرب . 

 أجد مقدار محصلة  القوى الكهربائية المؤثرة  في الشحنة

واتجاهها بيانيا.

الحل:

أ- نختار مقياس رسم مناسب مثلا (1cm:10N)  ,ونرسم ثلاث

 متجهات  ليكون طول كل متجه $F_1:2cm , F_2=3cm, F_3=5cm$

 ب - نرسم متجه القوة الأول F_{1 ،}   ثم نرسم سهم متجه القوة

 الثاني F₂ بحيث يقع ذيله عند رأس سهم F₁  ثم نرسم سهم 

  متجه القوة  الثالث F₃ بحيث يقع ذيله عند  رأس المتجه الثاني .

ج- نرسم  المحصلة من ذيل المتجه الأخير إلى رأس المتجه الأول 

د- نقيس بالمسطرة  طول متجه المحصلة R  ويساوي 6.4Cm

 وبحسب مقياس الرسم  تكون المحصلة : 

   $R=6.4\times \frac{100cm}{1N}=640N$

ونقيس بالمنقلة الزاوية بين متجه المحصلة ومحور x+ بعكس دوران

 عقارب الساعة $\theta ={173}^{\circ }$

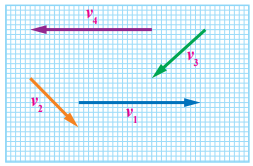
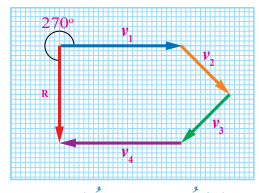
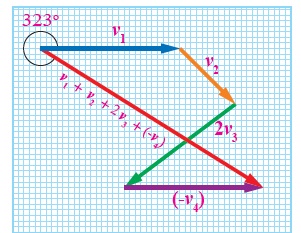
 مثال 11:مثلت أربعة متجهات  للسرعة $\mathbf{(}{\mathbf{v}}_{\mathbf{1}}\mathbf{ }\mathbf{ }\mathbf{,}{\mathbf{v}}_{\mathbf{2}\mathbf{ }\mathbf{ }}\mathbf{,}\mathbf{ }\mathbf{ }{\mathbf{v}}_{\mathbf{3}\mathbf{ }\mathbf{ }\mathbf{ }}\mathbf{,}{\mathbf{v}}_{\mathbf{4}}\mathbf{)}$بالرسم

كما في الشكل. وذلك باستخدام مقياس الرسم  ($1cm:5m/s$)  أجد:   

 أ- مقدار متجه  محصلة السرعة ، واتجاهه.

ب-   V₁+V₂ +2V₃ - V₄

 الحل: 

أ- نطبق طريقة المضلع بحيث نرسم كل متجه عند رأس السابق

  له ثم نرسم المحصلة من ذيل الاخير الى راس الاول،  ثم نقيس

 طول المحصلة بالمسطرة  R=4Cm.,وبحسب مقياس الرسم

  تكون المحصلة   R=20m/s,270^o  واتجاهها نحو  الجنوب

ب- نطبق طريقة المضلع مع ضرب المتجه v₃  x2  وعكس

اتجاه المتجه v₄  تكون المحصلة كما في الشكل  ويكون  مقدار

  المحصلة  R =10x5=50m/s واتجاهها يميل بزاوية ($\theta$ )   مقدارها 323^o 

 كما في  الشكل  المقابل.

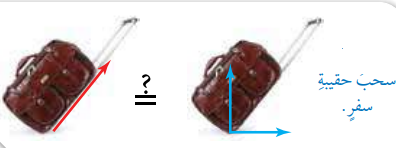
فمثلا في الشكل المقابل نلاحظ أن سحب الحقيبة

بشكل مائل يكافيء تحريكها  مسافة افقية للأمام

وعموديا  نحو الاعلى. أي أن القوة تكافي مجموع

 قوتين أحدهما أفقية  والاخرى عمودية .

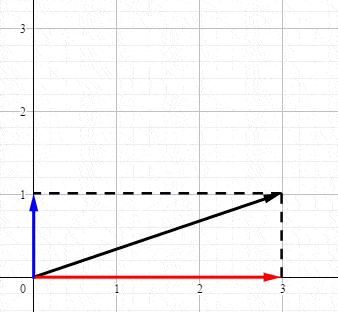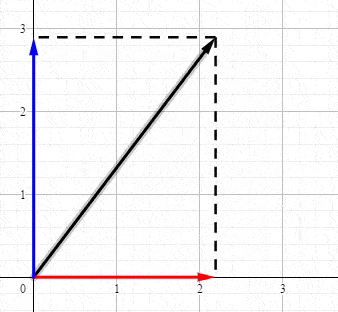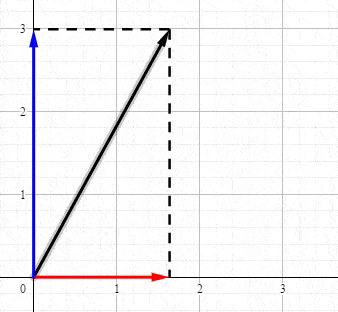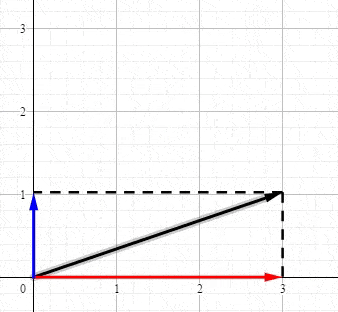
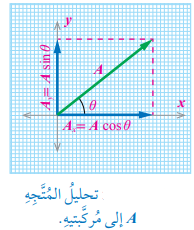
فمثلا يمكن تحليل المتجه A في الشكل الى مركبتين:    

• مركبة أفقية A_x : تمثل مسقط المتجه A على محور x+.
• مركبة عمودية Ay : تمثل مسقط المتجه A على محور y+.

ويكون  المجموع المتجهي  للمركبتين مساوي  المتجه A 

                                 ${\mathit{A}}_{\mathbf{x}}\mathbf{+}{\mathit{A}}_{\mathbf{y}}\mathbf{=}\mathit{A}$

ولحساب  قيم  المركبات نستخدم النسب المثلثية                                        

                $\cos \theta =\frac{A_x}{A_{}}\to A_x=A \cos \theta$

                 $\sin \theta =\frac{A_y}{A}\to A_y= A \sin \theta$  

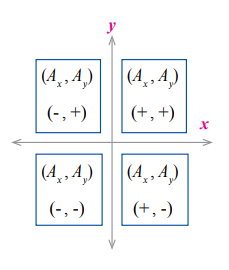
تتغير اشارة المركبات الأفقية والعمودية بحسب الربع الذي يقع فيه المتجه.

كما يوضح الشكل المقابل

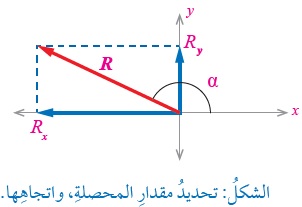
ويمكن  حساب مقدار المتجه A من مركبتيه (A_x , A_y) باستخدام

 نظرية فيثاغورس:    $A=\sqrt{A_x^2+A_y^2}$

أما الزاوية المرجعية $\theta$ بين المتجه ومحور x+, فيمكن حسابها

 من العلاقة؛

                           $tan\theta = \frac{A_y}{A_{x }}\to \theta =ta{n}^{-1} \frac{A_y}{A_x}$

وباستخدام هذه العلاقة سنحصل على قيمتين للزاوية $\theta$ نختار 

أحدهما حسب الربع الذي تقع فيه وحسب اشارة المركبتين

 كما في الشكل السابق.

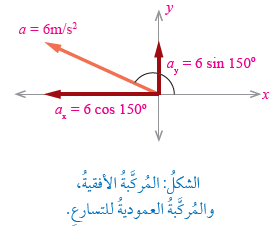
المثال 12:

تتحرَّكُ مركبةٌ بتسارُعٍ ثابتٍ ( a = 6 m/s² , 150^o ). أَجِدُ مقدارَ

المُركَّبتيْنِ الأفقيةِ والعموديةِ للتسارعِ، ثمَّ أُحدِّدُ اتجاهَ
كلٍّ منْهُما.
المعطياتُ:(a_x = 6 m/s² , 150^o)
المطلوبُ: ?    ?=a_y

  _{الحل: أتذكر  أن: $\cos (\hspace{0.17em}{180}^o-\theta ) =-\cos \theta , \sin ( {180}^o-\theta ) = \sin \theta$}

المُركَّبةُ الأفقيةُ: 

  $a_{x }= a\cos \theta = 6\times \cos \times {150}^0 =6( - \cos {30}^0)= -6\times 0.87 = -5.2m/s^2$
المُركَّبةُ العموديةُ: 

  $a_y = a \sin \theta =6\times \sin 150 = 6\times \sin {30}^{o }=6\times 0.8 =3m/s^2$

يُلاحَظُ أنَّ إشارةَ a_𝑥 سالبةٌ؛ ما يعني أنَّ اتجاهَها هوَ في اتجاهِ (𝑥-)،

وأنَّ إشارةَ a_𝑦 موجبةٌ؛ ما يعني أنَّ  اتجاهَها هوَ في اتجاهِ ( 𝑦+)،

حيثُ إنَّ المُتَّجِهَ a يقعُ في الربعِ الثاني. أنظرُ الشكلَ المقابل.

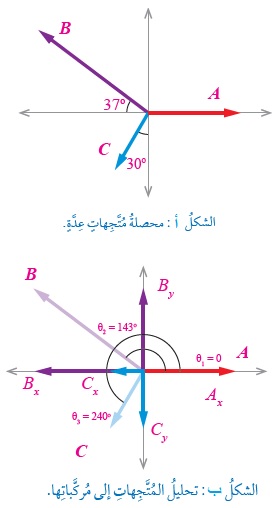
 المثال 14:

ثلاثة متجهات (A,B,C)  قيمها (3u, 5u,2u)  على الترتيب كما

 في الشكل أ .

أجد مقدار المحصلة واتجاهها  بالطريقة التحليلية.

الحل: 

أُحلِّلُ كلَّ مُتَّجِهٍ إلى مُركَّبتيهِ: المُركَّبةِ الأفقيةِ على محورِ x،

 والمُركَّبةِ العموديةِ على محورِ y، كمافي الشكلِ (ب)، على

 النحوِ الآتي:

نحلل كل متجه الى مركبتيه.

                                        Ax = A cos θ₁ = 3 cos 0^o = 3 × 1= 3

                                         Ay = A sin θ₁ = 3 sin 0^o = 3 × 0= 0   

                        Bx = B cos θ₂ = 5 cos 143^o = 5 × -0.8 = - 4 u

                             By = B sin θ₂ = 5 sin 143^o = 5 × 0.6 = 3 u

                         Cx = C cos θ₃ = 2 cos 240^o = 2 ×- 0.5 = -1 u

                    Cy = C sin θ₃ = 2 sin 240^o = 2 ×- 0.87 = -1.74 u

ثم أجد مجموع المركبة الأفقية على محور( x): 

              باتجاه ( -x )                  Rx = Ax + Bx + Cx
                                               $= 3 -4 -1 = -2 u$   

ثم أجد مجموع المركبة  الرأسية على محمور (y): 

                باتجاه ( +Y)                            Ry = Ay + By + Cy 

                                            $= 0 + 3 -1.74=1.26 u$ 

وحسب نظرية فيثاغورس، نجد مقدار المحلصة ( لاحظ الشكل المقابل): 

                               $$\begin{gathered} R=\sqrt{R_x^2+R_y^2}=\sqrt{(-2^2+1.{26}^2) } \\ =2.36u \end{gathered}$$  

 وأجد الاتجاه:

                                                                              $$\begin{gathered} \alpha ={\tan }^{-1}\frac{1.26}{-2} \\ \alpha ={148}^{\circ },{328}^{\circ } \end{gathered}$$ 

تمرين صفحة 33:

تُؤثِّرُ ثلاثُ قوى في نقطةٍ ماديةٍ كما في الشكلِ المقابل

 إذا كانَتْ محصلةُ هذهِ القوى صِفرًا، فما مقدارُ كلٍّ منَ

 القُوَّتَيْنِ الأولى والثانيةِ؟  

المعطيات : الشكل المقابل:

الحل: 

عندما  تكون  القوة  المحصلة صفر، فإن:

                                        $\underset{ }{\sum F_x =0 , {\displaystyle \sum _{ }}{F}_y =0}$    

القوة  المحصلة بالاتجاه الأفقي ( x ) : 

        $F_3\cos {30}^0 - F_2 = 50\times 0.87 - F_2 =0 \Rightarrow F_2 =43.5N$ 

القوة  المحصلة بالاتجاه ( y ) :    

        $F_1 - F_3\sin {30}^o=F_1 - 50\times 0.5=0 \Rightarrow F_1 = 25N$