رياضيات فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 122

أَرْسُمُ قِطْعَةً مُسْتَقيمَةً طولُها $6 cm$ ، ثُمَّ أُنْشِئُ مُنَصِّفًا عَمودِيًّا لَها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

الحل : 

الخطوة 1 : أرسم قطعة مستقيمة طولها $6 cm$ وأسميها$\overline{AB}$
الخطوة 2 : أفتح الفرجار فتحةً تزيد على نصف القطعة المرسومة $\overline{AB}$ ثمّ أثبت رأسه عند النقطة A ، ثم أرسم قوسًا كبيرًا يقطع القطعة $\overline{AB}$
الخطوة 3 : أضع رأس الفرجار عند النقطة B من دون تغيير مقدار فتحته ، ثم أرسم قوسًا كبيرًا آخر يقطع القطعة $\overline{AB}$ ، فيتقاطع القوسان في نقطتين (إذا لم يتقاطع القوسان مرتين ، فأتأكد أنهما انمتدا على نحوٍ كافٍ.)
الخطوة 4 : أرسم خطًا مستقيمًا يمر بنقطتي تقاطع القوسين ، ويُعدّ المُنصف العمودي للقطعة .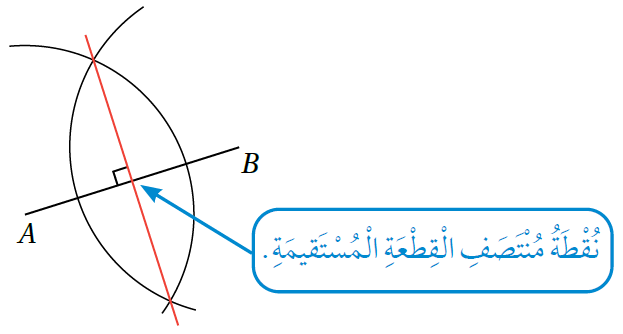

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

أتحقق من فهمي صفحة 123

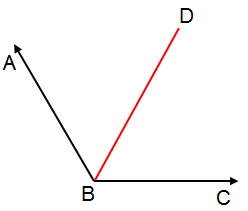
أَرْسُمُ زاوِيَةً قِياسُها ° 120 ، ثُمَّ أُنَصِّفُها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

الحل : 

الْخُطْوَةُ 1 :  أَسْتَعْمِلُ الْمِنْقَلَةَ لِرَسْمِ زاوِيَةٍ قِياسُها ° 120 ، وَأُسَمّيها B الْخُطْوَةُ 2 :  أُثَبِّتُ رَأْسَ الْفِرْجارِ عِنْدَ رَأْسِ الزّاوِيَةِ A ثُمَّ أَرْسُمُ قَوْسًا يَتَقاطَعُ مع ضلعي $\angle B$ ، ثُمَّ أُسَمّي نُقْطَتَيِ التَّقاطُعِ A , C  الْخُطْوَةُ 3 : أُثَبِّتُ رَأْسَ الْفِرْجارِ عِنْدَ النُّقْطَةِ A ، ثمّ أرسم قوسًا داخل$\angle B$ الْخُطْوَةُ 4 : أُثَبِّتُ رَأْسَ الْفِرْجارِ عِنْدَ النُّقْطَةِ C ، من دون تغيير مقدار فتحته ثمّ أرسم من النقطة C قوسًا يقطع القوس المرسوم   الْخُطْوَةُ 5 : أسمي نقطة تقاطع القوسين D ، وأستعمل المسطرة لرسم منصف الزاوية بدءًا بالنقطة B ومرورًا بالنقطة D

 

 

 

 

 

 

 

 

 

 

 

---

 

أتحقق من فهمي صفحة 124

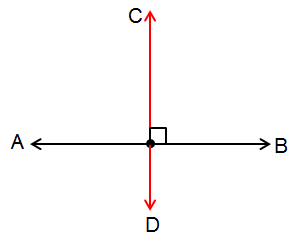
أَرْسُمُ بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ مُسْتَقيمًا عَمودِيًّا عَلى الْقِطْعَةِ المستقيمة  AB  مِنَ النُّقْطَةِ C

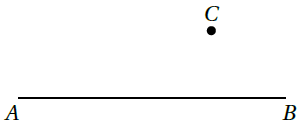
الحل : 

الْخُطْوَةُ 1 : أفتح الفرجار فتحة مناسبة ، ثمّ أثبت رأسه عند النقطة C، ثمّ أرسم قوسًا يقطع المستقيم AB في نقطتين وأسميهما    الْخُطْوَةُ 2 : أفتح الفرجار فتحة تزيد عن نصف المسافة AB ثمّ أرسم قوسًا من النقطة A ، ثمّ أرسم قوسًا آخر من النقطة B ، على أن يتقاطع القوسان في نقطة وأسميها   الْخُطْوَةُ 3 : أستعمل المسطرة لرسم المستقيم المار بنقطتي التقاطع من أعلى ومن أسفل فينتج المستقيم C العمودي على المستقيم AB

 

 

 

 

 

 

 

 

 

---

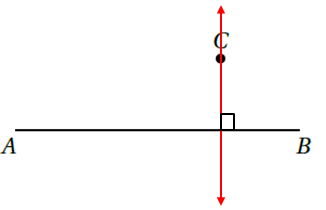أتحقق من فهمي صفحة 125

أَرْسُم مُستقيمًا عموديًّا عَلى القطعة الْمُستَقيمة AB من النّقطة  D 

الحل : 

الْخُطْوَةُ 1 : أفتح الفرجار فتحة مناسبة ، ثمّ أثبت رأسه عند النقطة D ، ثمّ أرسم قوسًا يقطع المستقيم AB في النقطتين ، وأسميهما  الْخُطْوَةُ 2 : أفتح الفرجار فتحة تزيد عن نصف المسافة AB ، ثمّ أرسم قوسًا من النقطة A   ثمّ أرسم قوسًا آخر من النقطة B على أن يتقاطع القوسان في نقطة وأسميها (C)   الْخُطْوَةُ 3 : أستعمل المسطرة لرسم المستقيم المار بالنقطتين C , D  ، فينتج المستقيم $\overleftrightarrow{DC}$ العمودي على المستقيم AB

 

 

 

 

 

 

 

 

 

---

 

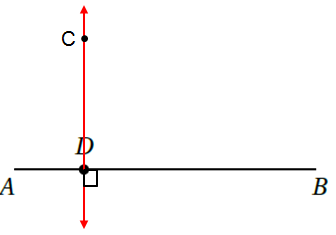أتحقق من فهمي صفحة 126

أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمُثَلَّثَ الْقائِمَ الزّاوِيَةِ لِرَسْمِ مُسْتَقيمٍ مُوازٍ لِلْمُسْتَقيمِ $\overleftrightarrow{MN}$ ، ويمر بالنقطة E

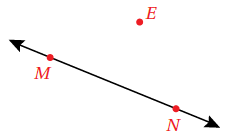
الحل : 

الْخُطْوَةُ 1 : أضع أحد طرفي الزاوية القائمة للمثلث القائم على المستقيم $\overleftrightarrow{MN}$  ثمّ أضع المسطرة مُلاصقة للضلع الآخر للزاوية القائمة بحيث يكون صفر تدريج المسطرة على الخط تمامًا. الْخُطْوَةُ 2 : أحرك المسطرة إلى أعلى حتى يصل إلى حرف E   ثمّ أرسم قطعة مستقيمة أسفل المثلث. الْخُطْوَةُ 3 : أكمل رسم القطعة إلى مستقيم باستعمال المسطرة ،  فينتج المستقيم الموازي للمستقيم $\overleftrightarrow{MN}$ ويمر بالنقطة E

 

 

 

 

 

 

---

 

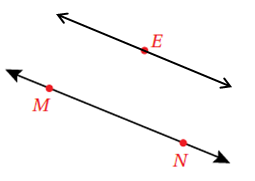أسئلة أتدرب وأحل المسائل 

1)  أَرْسُمُ قِطْعَةً مُسْتَقيمَةً طولُها $12 cm$، ثُمَّ أُنْشِئُ مُنَصِّفًا عَمودِيًّا لَها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

الحل : 

 
2)  أَرْسُمُ زاوِيَةً حادَّةً، ثُمَّ أُنَصِّفُها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

الحل :

قياس الزاوية الحادة أقل من $90°$ ، قياس $\angle CGF$ يساوي $60°$

---

3) أَرْسُمُ زاوِيَةً قِياسُها ° 80 ، ثُمَّ أُنَصِّفُها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

---

4) أَرْسُمُ زاوِيَةً مُنْفَرِجَةً، ثُمَّ أُنَصِّفُها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

الحل :

قياس الزاوية المنفرجة أكثر من $90°$  وأقل من $180°$  ، قياس $\angle LMN$ يساوي $140°$

---

 

5)   أَرْسُمُ مُسْتَقيمًا عَمودِيًّا عَلى الْمُسْتَقيمِ $\overleftrightarrow{AB}$من النقطة c

الحل :

---

 

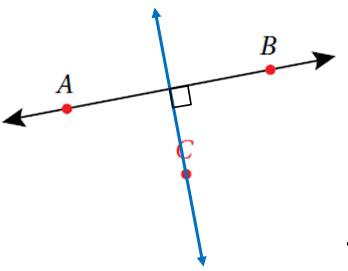
6) أَرْسُمُ مُسْتَقيمًا عَمودِيًّا عَلى الْمُسْتَقيمِ $\overleftrightarrow{GH}$من النقطة J .

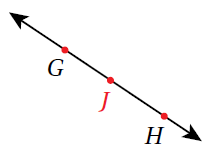
الحل :

---

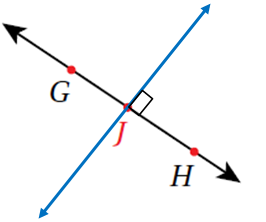
7)  أَستعملُ المِسطرةَ والمُثلث الْقائِم الزّاوية لرَسم مُستقيمٍ مُوازٍ لِلمُستقيمِ $\overleftrightarrow{AB}$ ، ويبعدُ عنهُ مسافة 6cm    

الحل :

---

8) كَم مُستقيمًا يُمكن رَسمهُ بحيثُ يَكون مُوازيًا لِلْمُستقيم $\overleftrightarrow{AB}$  ومارًا بالنقطة c ؟

الحل :

مستقيم واحد فقط . 

---

 

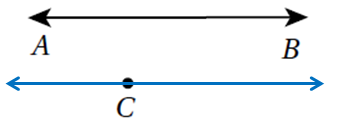
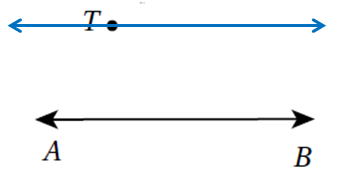
وَقَفَ مُحَمَّدٌ عِندَْ النقُّْطَةِ T مُواجِهًا الشّارِعَ الَّذي يُمَثِّلُهُ الْمُسْتَقيمُ AB في الشَّكْلِ الْآتي: 

9) أَرْسُمُ الْقِطْعَةَ الْمُسْتَقيمَةَ الَّتي تُمَثِّلُ أَقْصَرَ مَسافَةٍ يَقْطَعُها مُحَمَّدٌ لِلْوُصولِ إِلى الشّارِعِ.

الحل :

أرسم عمود من موقع محمد إلى الشارع .

---

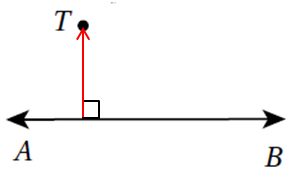
10) أَرْسُمُ الْمُسْتَقيمَ الَّذي يُمَثِّلُ الطَّريقَ الَّذي يَسْلُكُهُ مُحَمَّدٌ مِنْ دونِ أَنْ يَقْطَعَ الشّارِعَ مَهْما ابْتَعَدَ. 

الحل :

أرسم مستقيم يوازي المستقيم $\overleftrightarrow{AB}$ الذي يمثل الشارع .

---

 

يُمَثِّلُ الرَّسْمُ الْمُجاوِرُ شُعاعَيْنِ مُتَعامِدَيْنِ:

11) أَسْتَعْمِلُ الْفِرْجارَ لإنْشاءِ عَمودَيْنِ مُنَصِّفَيْنِ لِكُلٍّ  مِنَ الْقِطْعَتَيْنِ AB  و  BC  

الحل :

---

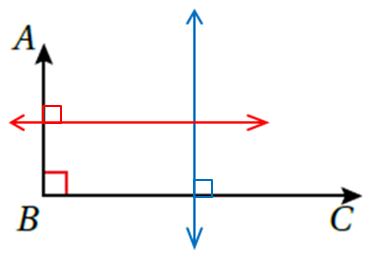
12) ما الشَّكْلُ الرُّباعِيُّ النّاتِجُ مِنْ رَسْمِ الْمُنصِّفين؟ أُوضِّح إِجابتي.

الإجابة : الشكل الناتج مستطيل ؛ لأن زوايا الشكل جميعها قائمة وكل ضلعين متقابلين متساويين ومتوازيين . 

---

13) مُنصف $\angle NPM$ هو $\overleftrightarrow{PQ}$ . أَكتبُ جُملةً عَدديّة تُمثّل العلاقة بين $m\angle NPM$ و $m\angle QPM$

الحل :

لأنّ $\overleftrightarrow{PQ}$ مُنصف للزاوية ؛ إذن : 

$m\angle QPM = \frac{1}{2} m\angle NPM$

---

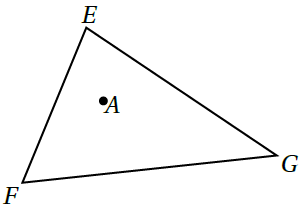
14) تَحَدٍّ : A  هِيَ نُقْطَةٌ داخِلَ الْمُثَلَّثِ EFG. أرسم من A  ثَلاثَةَ مُسْتَقيماتٍ، كُلٌّ مِنْها مُعامِدٌ لأحَدِ أَضْلاعِ الْمُثَلَّثِ  EFG  
مُسْتَعْمِلًا أَداةَ الْمُثَلَّثِ الْقائِمِ الزّاوِيَةِ.

 الحل :

---

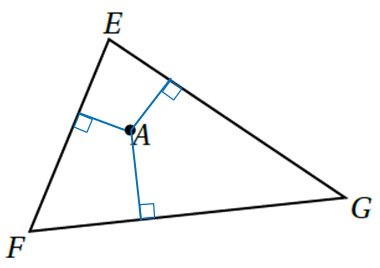
15) أَكْتَشِفُ الْخَطَأَ: يُظْهِرُ الرَّسْمُ الْمُجاوِرُ كَيْفَ حاوَلَ خالِدٌ رَسْمَ مُنَصِّفٍ عَمودِيٍّ لِقِطْعَةٍ بِاسْتِعْمالِ الْمِسْطَرَةِ، مُحَدِّدًا مُنْتَصَفَها بِالْقِياسِ، ثُمَّ رَسْمَ خَطٍّ مُسْتَقيمٍ يَمُرُّ بِهذا الْمُنْتَصَفِ. أُوَضِّحُ خَطَأَ خالِدٍ.

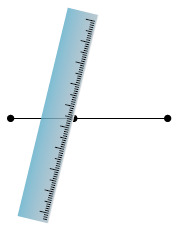
الإجابة : المُنصِف يجب أن يكون عمودي على القطعة المُنصَفة ، والزاوية التي تظهر من الرسم قياسها لا يساوي $90°$

---

 

 

أسئلة كتاب التمارين 

1) أَرْسُمُ قِطعةً مُستقيمةً طولُها $10 cm$، ثُمَّ أُنشئُ مُنصِّفًا عموديًّا لَها بِاستعمالِ المِسطرَة والفِرجارِ.

 الحل :

---

2) أَرْسُمُ زاوِيَةً قِياسُها ° 30 ، ثُمَّ أُنَصِّفُها بِاسْتِعْمالِ الْمِسْطَرَةِ وَالْفِرْجارِ.

 الحل :

---

3)  أَرْسُمُ مُسْتَقيمًا عَمودِيًّا عَلى الْقِطْعَةِ الْمُسْتَقيمَةِ CD مِنَ النُّقْطَةِ O

  الحل :

---

4) أَرْسُمُ مُسْتَقيمًا عَمودِيًّا عَلى الْقِطْعَةِ الْمُسْتَقيمَةِ PN مِنَ النُّقْطَةِ O   

 

 الحل :

---

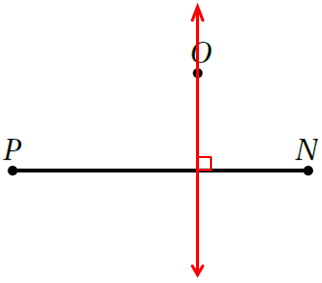
5) أَسْتَعْمِلُ الْمِسْطَرَةَ وَالْمُثَلَّثَ الْقائِمَ الزّاوِيَةِ لِرَسْمِ مُسْتَقيمٍ مُوازٍ لِلْمُسْتَقيمِ $\overleftrightarrow{AB}$  وَيَبْعُدُ عَنْهُ مَسافَةَ $6 cm$  

 الحل :

---

 

6) نَصَّفتْ سَميرةُ الزاويةَ ABC باستعمال الفرجارِ كما في الشَّكلِ الْمُجاورِ. ماخَطأُ سَميرةَ؟ أُبرِّرُ إِجابتي.

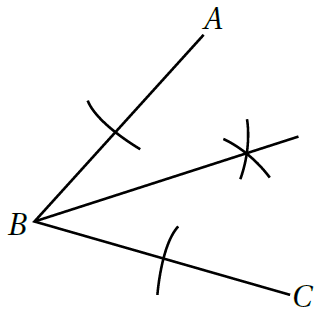
الإجابة : خطأ سميرة أنها ركزت رأس الفرجار في النقطة A ، والنقطة C ورسمت القوسين على الضلعين ، بينما الصحيح أن تركز رأس الفرجار في رأس الزاوية النقطة B وترسم القوسين .

---

يُبَيِّنُ الرَّسْمُ الْمُجاوِرُ الْقِطْعَتَيْنِ الْمُسْتَقيمَتَيْنِ $\overleftrightarrow{AB} , \overleftrightarrow{BC}$ أستعْمِلُ الْمِسْطَرَةَ وَالْفِرْجارَ لإنْشاءِ:

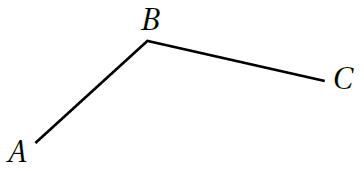
7) مُنَصِّفٍ عَمودِيٍّ لِلْقِطْعَةِ الْمُسْتَقيمَةِ AB ،ثُمَّ أُسَمّي نُقْطَةَ الْمُنْتَصَفِ M.  

 الحل :

---

 

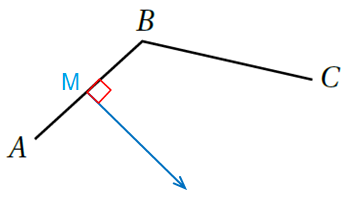
8) مُنَصِّفٍ عَمودِيٍّ لِلْقِطْعَةِ الْمُسْتَقيمَةِ BC ، ثُمَّ أُسَمّي نُقْطَةَ الْمُنْتَصَفِ N.

 الحل :

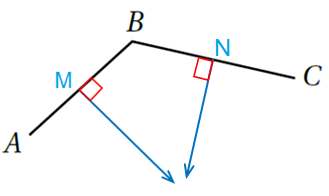
9) مُنَصِّفٍ عَمودِيٍّ لِلْقِطْعَةِ الْمُسْتَقيمَةِ MN ، ثُمَّ أُسَمّي نُقْطَةَ الْمُنْتَصَفِ Q.

 الحل :

---

 

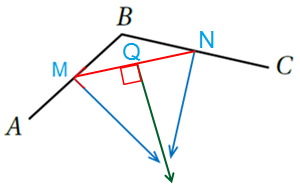
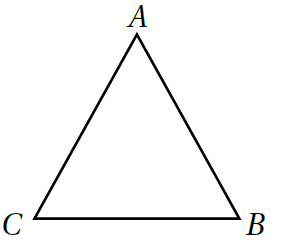
يُمثِّلُ الشَّكل المُجاورُ المُثلث ABC : 

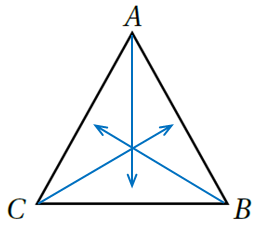
10) أَسْتَعْملُ المِسطرةَ وَالْفِرجار لإنشاءِ مُنَصِّفاتٍ لِكُلِّ زاوِيةٍ من زوايا المثلث.

الحل :

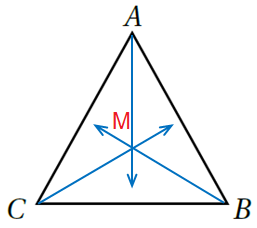
11) هَلْ تَلْتَقي الْمُنَصِّفاتُ في نُقْطَةٍ واحِدَةٍ؟ إِذا كانَ الْجَوابُ بِالْايجابِ، فَأُعَيِّنُها.

 الحل :

نعم تلتقي منصفات الزوايا في نقطة واحدة. 

---

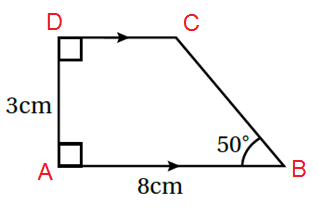
12)  أَرْسُمُ شِبْهَ الْمُنْحَرِفِ الْمُجاوِرَ.

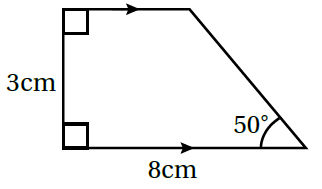
 الحل :

أرسم المستقيم AB طوله يساوي$8cm$ .

من النقطة A أقيم عمود طوله $3cm$ ، ومن النقطة B ، أرسم زاوية قياسها $50°$ 

أرسم من النقطة D مستقيم يوازي المستقيم AB  

أمد المستقيم DC حتى يلتقي بالمستقيم (الضلع الآخر للزاوية) في النقطة C.