رياضيات 10 فصل ثاني

أتحقق من فهمي صفحة 132

أحدد إذا كان الحادثان متنافيين أم لا في ما يأتي ، مبررا إجابتي : 

a ) التجربة هي سحب بطاقة واحدة عشوائيًا من سلة فيها 5 بطاقات حمراء ، و 3بطاقات خضراء . الحادث الأول سحب بطاقة حمراء ، والحادث الثاني سحب بطاقة خضراء . 

b)  التجربة هي إلقاء حجر نرد منتظم . الحادث الأول هو الحصول على عدد فردي والثاني هو الحصول على عدد زوجي .

الحل 

(a

الحادثان متنافيان ؛ لأنه لا يمكن سحب بطاقة لونها أحمر و أخضر في المرة الواحدة .

b) 

الحادثان متنافيان ؛ لأن الأعداد الفردية على حجر النرد هي : 1 , 3 ,5 , والأعداد الزوجية عليه هي : 2 ,4 ,6، ولا توجد عناصر مشتركة بين الحادثين 

---

 

أتحقق من فهمي صفحة 133

في تجربة اختيار عدد عشوائيًا من بين الأعداد :  8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 أجد 

a ) احتمال اختيار عدد أولي ، ويقبل القسمة على 4

b ) احتمال اختيار عدد أولي ، أو عدد يقبل القسمة على 4 

الحل 

ليكن الحادث A : اختيار عدد أولي 

  والحادث B : اختيار عدد يقبل القسمة على 4 

 

 

---

 

أتحقق من فهمي صفحة 135 

في تجربة اختيار عدد عشوائيًا من المجموعة $\left\{ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10\right\}$ أجد

a) احتمال اختيار عدد أولي ، ومن عوامل العدد 10

b) احتمال اختيار عدد أولي ، أو عدد من عوامل العدد 10

الحل 

ليكن الحادث A  اختيار عدد أولي  والحادث B اختيار عدد من عوامل 10

إذا ، 

$\mathit{A}\mathbf{ }\mathbf{=}\mathbf{\{}\mathbf{ }\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{3}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{7}\mathbf{\}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{B}\mathbf{ }\mathbf{=}\mathbf{\{}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{10}\mathbf{\}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{\{}\mathbf{2}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{\}}$

 

أي أن الحادثين A , B غير متنافيين 

 

$\mathit{a}\mathbf{)}\mathbf{ }\mathit{P}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{ }\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{2}}{\mathbf{10}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{1}}{\mathbf{5}}\mathbf{ }$

$\mathit{b}\mathbf{)}\mathit{P}\mathbf{ }\mathbf{(}\mathit{A}\mathbf{\cup }\mathit{B}\mathbf{)}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{P}\mathbf{(}\mathit{A}\mathbf{)}\mathbf{ }\mathbf{+}\mathbf{ }\mathit{P}\mathbf{(}\mathit{B}\mathbf{)}\mathbf{ }\mathbf{-}\mathbf{ }\mathit{P}\mathbf{ }\mathbf{(}\mathbf{ }\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{)}\mathbf{ }\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{4}}{\mathbf{10}}\mathbf{+}\mathbf{ }\frac{\mathbf{4}}{\mathbf{10}}\mathbf{ }\mathbf{-}\mathbf{ }\frac{\mathbf{2}}{\mathbf{10}}\mathbf{ }\mathbf{=}\mathbf{ }\frac{6}{\mathbf{10}}\mathbf{=}\frac{3}{\mathbf{5}}$                                                                              

---

 

أتحقق من فهمي صفحة 136 

سحب هيثم كرة عشوائيًا من كيس يحتوي على كرات متماثلة ؛ واحدة منها صفراء ، و 3 كرات حمراء ، و 12 كرة خضراء . ما احتمال عدم سحب هيثم كرة خضراء ؟ 

ليكن الحادث A سحب كرة خضراء 

إذا المطلوب هو $\mathit{P}\mathbf{ }\mathbf{\left(}\overline{\mathbf{A}}\mathbf{\right)}\mathbf{ }$

---

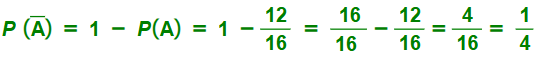
أتدرب و أحل المسائل 

أحدد إذا كان الحادثان متنافيين أم لا لكل تجربة عشوائية في ما يأتي ، مبررا إجابتي : 

1. ظهور العدد 3 / أو ظهور عدد زوجي عند إلقاء حجر نرد منتظم مرة واحدة . 

2. ظهور أحد عوامل العدد 12 , أو ظهور عدد أولي عند إلقاء حجر نرد منتظم مرة واحدة .

3. ظهور عددين مجموعهما 8 أو 12 عند إلقاء حجري نرد منتظم مرة واحدة . 

الحل : 

1. 

الحادثان متنافيان ؛ لأنه لا توجد عناصر مشتركة بينهما 

2.

الحادثان غير  متنافيان ؛ لأنه 2 و 3 عناصر مشتركة بينهما 

3. 

الحادثان متنافيان ؛ لأنه لا توجد عناصر مشتركة بينهما 

---

في تجربة اختيار بطاقة واحدة عشوائيًا من 20 بطاقة متماثلة ، كتب على كل منها عدد من 1 إلى 20 ، أجد : 

4. احتمال اختيار عدد من مضاعفات العدد 7 ، ومن مضاعفات العدد 5 

5. احتمال اختيار عدد من مضاعفات العدد 7 ، أو من مضاعفات العدد 5

6. احتمال اختيار عدد فردي ، ويقبل القسمة على 4 

7. احتمال اختيار عدد فردي أو يقبل القسمة على 4

الحل :

4) 

A : عدد من مضاعفات 7

B : عدد من مضاعفات 5

إذا 

$\mathit{A}\mathbf{=}\mathbf{ }\mathbf{\{}\mathbf{ }\mathbf{7}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{14}\mathbf{\}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{B}\mathbf{ }\mathbf{=}\mathbf{\{}\mathbf{ }\mathbf{5}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{10}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{15}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{20}\mathbf{\}}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathit{P}\mathbf{ }\mathbf{(}\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{)}\mathbf{=}\mathbf{\varnothing }$

 

 

 

---

مجموعة من الكرات المتماثلة ، مرقمة من 1 إلى 21 ، وموضوعة داخل صندوق . 

إذا اختبرت كرة من الصندوق عشوائيًا ، فأجد مستعملا أشكال فن : 

8. احتمال أن تحمل الكرة عدد زوجيًا 

9 . احتمال أن تحمل الكرة عددَا من مضاعفات العدد 3

10. احتمال أن تحمل الكرة عددًا زوجيًا ،  ومن مضاعفات العدد 3

11 . احتمال أن تحمل الكرة عددًا زوجيًا ، أو من مضاعفات العدد 3 

الحل : 

A : عدد زوجي 

B: عدد من مضاعفات 3

إذا 

 

 

---

 طب : في دارسة طبية شملت 100 شخص ، زار بعضهم طبيب الأسرة أو طبيب أسنان في أحد الأسابيع كما هو مبين في شكل فن المجاور . إذا اختير أحدهم عشوائيًا ، فأجد احتمال كل حادث مما يأتي : 

12. أن يكون الشخص قد زار طبيب الأسنان 

13. أن يكون الشخص قد زار طبيب الأسرة . 

14.  أن يكون الشخص قد زار طبيب الأسنان و طبيب الأسرة 

15 . أن يكون الشخص قد زار طبيب الأسنان أو طبيب الأسرة 

16 . عدم زيارة الشخص طبيب الأسنان 

17. عدم زيارة الشخص طبيب الأسرة 

الحل : 

A : شخص زار طبيب الأسنان 

B : شخص زار طبيب الأسرة 

إذاً 

 

 

---

رياضة  : سئل 60 رياضيًا إذا كانوا يمارسون لعبة كرة القدم أو كرة السلة ، وقد توزعوا وفق إجاباتهم كما في الجدول الآتي : 

إذا اختير رياضي منهم عشوائيًا ، فاستعمل أشكال فن لإيجاد : 

18. احتمال أن يكون ممن يمارسون لعبتي كرة القدم وكرة السلة 

19 . احتمال أن يكون ممن يمارسون لعبة القدم ، ولا يمارسون لعبة كرة السلة .

20 . احتمال أن يكون ممن يمارسون لعبة كرة السلة ، ولا يمارسون لعبة كرة القدم . 

21 . احتمال أن يكون ممن لا يمارسون لعبة كرة القدم ، ولا يمارسون لعبة كرة السلة .

الحل 

 

A : لاعب يمارس كرة القدم 

B : لاعب يمارس كرة السلة 

إذًا 

 

---

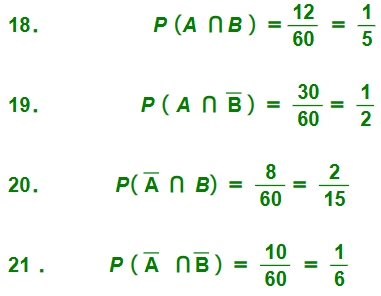
22 . تجارة : أحل المسألة الواردة في بداية الدرس

استورد تاجر شحنة من السكر في باخرتين . إذا كان احتمال وصول الباخرة الأولى في موعدها %60 واحتمال وصول الباخرة الثانية في موعدها %50 ، واحتمال وصلهما معًا %30 فما احتمال وصول إحدى الباخرتين على الأقل في موعدها ؟ 

الحل : 

$\mathit{P}\mathbf{(}\mathit{A}\mathbf{\cup }\mathit{B}\mathbf{)}\mathbf{=}\mathit{P}\mathbf{\left(}\mathit{A}\mathbf{\right)}\mathbf{+}\mathit{P}\mathbf{\left(}\mathit{B}\mathbf{\right)}\mathbf{-}\mathit{P}\mathbf{(}\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{)}\mathbf{=}\mathbf{60}\mathbf{\%}\mathbf{+}\mathbf{50}\mathbf{\%}\mathbf{-}\mathbf{30}\mathbf{\%}\mathbf{=}\mathbf{ }\mathbf{80}\mathbf{\%}\mathbf{ }$

 

---

مهارات التفكير العليا 

23 . تحد : يوجد في إحدى المصانع 40عاملا ، منهم 24 عاملا يفضلون شرب الشاي وقت الاستراحة و 12 عاملا يفضلون شرب القهوة ، ولا يفضلون شرب الشاي فيها و 14 عاملا يفضلون شرب الشاي و لا يفضلون شرب القهوة فيها . 

إذا اختير أحد عمال المصنع عشوائيًا ، فما احتمال أن يكون ممن يفضلون شرب الشاي و شرب القهوة ؟ 

الحل : 

A : يفضلون شرب الشاي 

B : يفضلون شرب القهوة 

إذا 

$\mathit{P}\mathbf{(}\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{)}\mathbf{=}\frac{\mathbf{10}}{\mathbf{40}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{4}}$

 

---

24. أيهما لا ينتمي : في تجربة إلقاء حجر نرد منتظم مرة واحدة عشوائيًا ، كتبت الحوادث الآتية على بطاقات . أجد البطاقة المختلفة ، مبررًا إجابتي . 

الحل : 

 

ظهور عدد زوجي ، وهو أكبر من 2 ؛ لأنه حادث مركب ، أما بقية البطاقات فيظهر على كل منها حادث بسيط 

---

 

25. تبرير : قال هاني : إن احتمال فوز فريقه المفضل هو 0.3 فرد عليه يزيد قائلاً : إذا احتمال خسارة الفريق هو 0.7 هل قول يزيد صحيح ؟ مبررًا إجابتي .

الحل 

غير صحيح ؛ نظرًا لوجود احتمال تعادل الفريقين 

---

 

26 . مسألة مفتوحة : أصف موقفين من حياتي اليومية أحدهما يتضمن حادثين متنافيين و الآخر يتضمن حادثين غير متنافيين ، مبينًا كيف حددت ذلك .  

حسب إجابة الطالب 

1. الموقف الأول عند مباراة كرة القدم فالحادث الأول هو الفوز في المباراة و الحادث الثاني هو الخسارة 

هذان الحادثان متنافيان لأنه لا يمكن الفوز والخسارة في الوقت نفسه . 

 

2. الموقف الثاني عند إلقاء حجر نرد منتظم  فالحادث الأول الحصول على رقم زوجي أكبر من 4 والحادث الثاني الحصول على رقم من مضاعفات العدد 3

هذان الحادثان غير متنافيان 

فبفرض الحادث الأول A $A=\left\{6\right\}$ 

و الحادث الثاني B    $B=\{3,6\}$

فالحادثان مشتركان بالعنصر { 6} 

 

 

---

كتاب التمارين 

في تجربة اختيار عدد عشوائيا من بين الأعداد : 10 , 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 ,1 إذا كان (A) حادث اختيار عدد أكبر من 4 و (B) حادث اختيار عدد يقبل القسمة على 3 من دون باقٍ ، فأجد : 

1. احتمال اختيار عدد أقل من 4 ، ويقبل القسمة على 3

2. احتمال اختيار عدد أقل من 4 ، اويقبل القسمة على 3 

الحل 

                                                                  $\mathit{A}\mathbf{=}\mathbf{\{}\mathbf{1}\mathbf{,}\mathbf{2}\mathbf{,}\mathbf{3}\mathbf{\}}\mathbf{ }\mathbf{ }\mathbf{,}\mathbf{ }\mathit{B}\mathbf{=}\mathbf{\{}\mathbf{3}\mathbf{,}\mathbf{6}\mathbf{,}\mathbf{9}\mathbf{\}}$

                                                            $\mathbf{1}\mathbf{)}\mathbf{ }\mathbf{ }\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{=}\mathbf{\left\{}\mathbf{3}\mathbf{\right\}}\mathbf{ }\mathbf{\Rightarrow }\mathit{P}\mathbf{(}\mathbf{A}\mathbf{\cap }\mathbf{B}\mathbf{)}\mathbf{ }\mathbf{=}\frac{\mathbf{1}}{\mathbf{10}}$

$\mathbf{2}\mathbf{)}\mathbf{ }\mathit{P}\mathbf{(}\mathbf{A}\mathbf{\cup }\mathbf{B}\mathbf{)}\mathbf{=}\mathit{P}\mathbf{\left(}\mathbf{A}\mathbf{\right)}\mathbf{ }\mathbf{+}\mathit{P}\mathbf{\left(}\mathbf{B}\mathbf{\right)}\mathbf{ }\mathbf{-}\mathit{P}\mathbf{(}\mathbf{A}\mathbf{\cap }\mathbf{B}\mathbf{)}\mathbf{=}\frac{\mathbf{3}}{\mathbf{10}}\mathbf{ }\mathbf{+}\frac{\mathbf{3}}{\mathbf{10}}\mathbf{ }\mathbf{-}\frac{\mathbf{1}}{\mathbf{10}}\mathbf{ }\mathbf{=}\frac{\mathbf{5}}{\mathbf{10}}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}$

---

 

بين التمثيل البياني المجاور فضاء العينة $\Omega$ لتجربة عشوائية إذا كان  (A) يمثل النقاط الواقعة على المستقيم  x=3  وكان (B) يمثل النقاط الواقعة على المستقيم y = 5 -x  : 

 

3.  إذا اختيرت نقطة عشوائيا ، فما احتمال أن تقع على كلا المستقيمين :  x = 3 و y = 5 - x ؟ 

$\mathit{P}\mathbf{(}\mathit{A}\mathbf{\cap }\mathit{B}\mathbf{)}\mathbf{=}\frac{\mathbf{1}}{\mathbf{16}}$

 

---

الحل:

4) 

A: عدد من مضاعفات 7

B: عدد من مضاعفات 5

إذن،

$$\begin{gathered} A=\{7,14\} , B=\{5,10,15,20\} , A\cap B=\varnothing \\ P(A\cap B)=0 \end{gathered}$$

 

5)

$P(A\cup B)=P\left(A\right)+P\left(B\right)=\frac{2}{5}+\frac{4}{20}=\frac{6}{30}=\frac{3}{10}$

 

6)

C: عدد فردي.

D: عدد يقبل القسمة على 4

إذن،

$$\begin{gathered} C=\{1,3,5,7,9,11,13,15,17,19\} \\ D=\{4,8,12,16,20\} \\ C\cap D=\varnothing \\ P(C\cap D)=0 \end{gathered}$$

 

 

---

سئلت 516 مهندسة كهربائية و كيميائية  و مكانيكية عن المبحث المفضل  لكل منهن عندما كن في الصف العاشر وقد نظمت إجاباتهن في الجدول المجاور . 

إذا اختيرت مهندسة عشوائيًا من هذه العينة ، فما احتمال : 

9. اختيار مهندسة كهربائية تفضل مبحث العلوم ؟ 

$\frac{90}{516}$

10. اختيار مهندسة ميكانيكية تفضل مبحث الرياضيات ؟ 

$\frac{89}{516}$

11. اختيار مهندسة ميكانيكية ، أو مهندسة تفضل مبحث الرياضيات ؟ 

$\frac{335}{516}$

12. اختيار مهندسة لا تفضل مبحث الرياضيات ، لكنها ليست مهندسة كيميائية ؟ 

$\frac{171}{516}$

---