رياضيات أدبي فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 73

في تجربة سحب بطاقتين معًا عشوائيًّا من صندوق يحوي بطاقتين حمراوين وبطاقتين زرقاوين، إذا دلَّ المتغير العشوائي X على عدد البطاقات الزرقاء في السحبة، فأجد كلًّ ممّا يأتي: a) التوزيع الاحتمالي في صورة جدول. b) التوزيع الاحتمالي في صورة تمثيل بياني.

 

 

 

 

 

 

الحل : 

• عدد عناصر فضاء العيِّنة لهذه التجربة   3 = Ω   (لون البطاقيتين زرقاوين ، لون البطاقتين حمراوين ، لون البطاقتين مختلفتين ولا يهم الترتيب)   

• القيم التي يأخذها المتغير العشوائي X هي : 0 ، 1 ، 2  

• قِيَم اقتران التوزيع الاحتمالي للمتغير العشوائي X هي : 

$P (x = 0) = \frac{1}{3} , P (x =1) = \frac{1}{3} , P (x = 2) = \frac{1}{3}$  

a) التوزيع الاحتمالي في صورة جدول.

2	1	0	x
$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$	P(x)

 

 

 

b) التوزيع الاحتمالي في صورة تمثيل بياني.

---

 

 

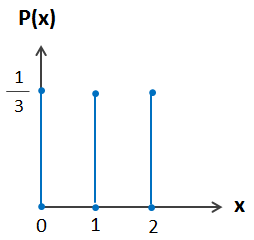
أتحقق من فهمي صفحة 74

في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي:

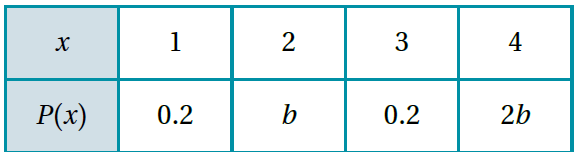
1)  أجد قيمة b.

2) أجد $P(2 \le x \le 4)$.

الحل : 

1)  أجد قيمة b.

لأنّ $\sum _{}P\left(x\right) = 1$	$0.2 + b + 0.2 + 2b = 1$
بتجميع الحدود المتشابهة	$3b + 0.4 = 1$
بطرح 0.4 من طرفي المعادلة	$3b = 0.6$
بقسمة طرفي المعادلة على3	$\mathit{b}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{2}$

 

 

 

 

 

2) أجد $P(2 \le x \le 4)$

بتحديد قِيَم المتغير العشوائي ضمن الشرط المُحدَّد	$P ( 2 \le x \le 4) = P(x=2) + P(x=3) + P(x=4)$
بتعويض قِيَم الاحتمالات	$= 0.2 + 0.2 + 0.4$
بالجمع	$\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{8}$

 

 

 

 

 

 

---

 

أتحقق من فهمي صفحة 75

في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي:

                                                                                                                                                         {(1, 2k), (2, 2k), (3, 3k), (4, 3k)}

1) أجد قيمة K .

2) أُنشِئ جدول التوزيع الاحتمالي.

3) أجد $P (x \ge 3)$.

الحل : 

1) أجد قيمة K .

لأنّ $\sum _{}P\left(x\right) = 1$	$2k +2k + 3k +3k = 1$
بتجميع الحدود المتشابهة	$10 k = 1$
بالتبسيط	$\mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{1}$

 

 

 

 

2) أُنشِئ جدول التوزيع الاحتمالي.

4	3	2	1	x
0.3	0.3	0.2	0.2	P(x)

 

 

 

3) أجد $P (x \ge 3)$

بتحديد قِيَم المتغير العشوائي ضمن الشرط المُحدَّد	$P (x \ge 3) = P(x=3) + P(x=4)$
بتعويض قِيَم الاحتمالات	$= 0.3 + 0.3$
بالجمع	$\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{6}$

 

 

 

 

 

---

 

أتحقق من فهمي صفحة 76

أحُلُّ المثال 4 إذا كان السحب مع الإرجاع.

مثال 4

في تجربة سحب ثلاث كرات عشوائيًّا على التوالي من دون إرجاع من كيس فيه 3 كرات حمراء، و 4 كرات خضراء، جميعها مُتماثِلة، إذا دلَّ المتغير العشوائي X على عدد الكرات الحمراء في السحبة، فأُنشِئ جدول التوزيع الاحتمالي للمتغير العشوائي x.

الحل : 

الخطوة 1 : أجد قِيَم المتغير العشوائي.

$X = \{ 0 , 1 , 2 , 3 \}$  

الخطوة 2 : أجد احتمالات قِيَم المتغير العشوائي ، باستخدام قانون الاحتمال

إذا كانت الكرات الثلاثة خضراء والسحب مع الإرجاع	$P(x=0) = \frac{4}{7}\times \frac{4}{7}\times \frac{4}{7} = \frac{64}{343}$
إذا كانت الكرات المسحوبة كرة واحدة حمراء وكرتين خضراء (يوجد ثلاث حالات)	$P(x=1) = 3 ( \frac{3}{7}\times \frac{4}{7}\times \frac{4}{7} )= \frac{144}{343}$
إذا كانت الكرات المسحوبة كرتين حمراوين وكرة واحدة خضراء (يوجد ثلاث حالات)	$P(x=2) = 3 ( \frac{3}{7}\times \frac{3}{7}\times \frac{4}{7} )= \frac{108}{343}$
إذا كانت الكرات المسحوبة الثلاثة حمراء	$P(x=3) = \frac{3}{7}\times \frac{3}{7}\times \frac{3}{7} = \frac{27}{343}$

 

 

 

 

 

 

 

 

 

 أُنشِئ جدول التوزيع الاحتمالي.

3	2	1	0	x
$\frac{27}{343}$	$\frac{108}{343}$	$\frac{144}{343}$	$\frac{64}{343}$	P(x)

 

 

 

---

 

أسئلة أتدرب وأحل المسائل

في تجربة إلقاء ثلاث قطع نقد متمايزة عشوائيًّا، دلَّ المتغير العشوائي X على عدد مرّات ظهور الصورة:

1) أجد التوزيع الاحتمالي في صورة جدول.

2) أجد التوزيع الاحتمالي في صورة تمثيل بياني.

الحل : 

• القيم التي يأخذها المتغير العشوائي X هي : 0 ، 1 ، 2 ، 3 

• قِيَم اقتران التوزيع الاحتمالي للمتغير العشوائي X هي :  

$P (x = 0) = \frac{1}{8} , P (x =1) = \frac{3}{8} , P (x = 2) = \frac{3}{8} , P (x = 3) = \frac{1}{8}$

1) أجد التوزيع الاحتمالي في صورة جدول.

3	2	1	0	x
$\frac{1}{8}$	$\frac{3}{8}$	$\frac{3}{8}$	$\frac{1}{8}$	P(x)

 

 

 

2) أجد التوزيع الاحتمالي في صورة تمثيل بياني.

 

---

 

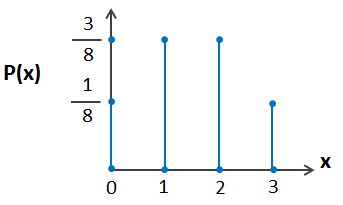
في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي:

       

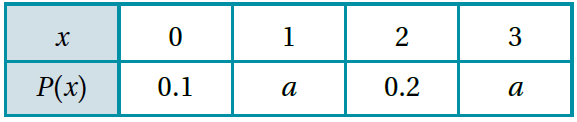
3) أجد قيمة a.   

4) أجد $P(1 < x \le 3)$         

الحل : 

3) أجد قيمة a.   

$$\begin{gathered} 0.1 + a + 0.2 + a = 1 \\ 2a + 0.3 = 1 \\ 2a = 0.7 \\ \Rightarrow \mathbf{ }\mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35} \end{gathered}$$

---

4) أجد $P(1 < x \le 3)$

$$\begin{gathered} P(1 < x \le 3) = P(x=2) + P(x=3) \\ = 0.2 + 0.35 \\ \mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{55} \end{gathered}$$

---

 

في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي:

                                                                                                                                                                                                                        {(0, 2k), (1, 0.5k), (2, 2k), (3, 0.5k)}

5) أجد قيمة K .

6) أُنشِئ جدول التوزيع الاحتمالي.

7) أجد $P( x \ge 2)$

الحل : 

5) أجد قيمة K . 

$$\begin{gathered} 2k + 0.5k + 2k + 0.5k = 1 \\ 5k = 1 \\ \mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{2} \end{gathered}$$

---

6) أُنشِئ جدول التوزيع الاحتمالي.

3	2	1	0	x
0.1	0.4	0.1	0.4	P(x)

 

 

 

---

7) أجد $P( x \ge 2)$

$$\begin{gathered} P( x \ge 2) = P(x=2) + P(x=3) \\ = 0.4 + 0.1 \\ \mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{5} \end{gathered}$$

---

 

8) في تجربة سحب كرتين عشوائيًّا على التوالي من دون إرجاع من صندوق يحوي 3 كرات حمراء مُرقَّمة من 1 إلى 3، و 3 كرات خضراء مُرقَّمة من 1 إلى 3،

جميعها مُتماثِلة، إذا دلَّ المتغير العشوائي X على عدد الكرات الحمراء في السحبة، فأُنشِئ جدول التوزيع الاحتمالي للمتغير العشوائي x.   

 الحل :   

القيم التي يأخذها المتغير العشوائي :  𝑋 = { 0 , 1 , 2 , 3 }

احتمالات قِيَم المتغير العشوائي.

0 كرة حمراء ، و 2 كرة خضراء	$P (x = 0) = \frac{ {}_{3}C_0 \times {}_{3}C_2}{ {}_{6}C_2} = \frac{1}{5}$
1 كرة حمراء ، و 1 كرة خضراء	$P (x = 1) = \frac{ {}_{3}C_1 \times {}_{3}C_1}{ {}_{6}C_2} = \frac{3}{5}$
2 كرة حمراء ، و 0 كرة خضراء	$P (x = 2) = \frac{ {}_{3}C_2 \times {}_{3}C_0}{ {}_{6}C_2} = \frac{1}{5}$

 

 

 

 

 

 

 

 

جدول التوزيع الاحتمالي للمتغير العشوائي x. 

2	1	0	x
$\frac{1}{5}$	$\frac{3}{5}$	$\frac{1}{5}$	P(x)

 

 

 

---

 

9) أحُلُّ المسألة الواردة في بند (مسألة اليوم).

مسألة اليوم : عند إلقاء حجري نرد متمايزين مرَّة واحدة، وتسجيل مجموع العددين الظاهرين، ما المجموع الذي احتماله أكبر؟

الحل : 

المجموع 7 هو المجموع ذو الاحتمال الأكبر والذي يساوي $\frac{6}{36} =\frac{1}{6}$

---

 

10) مواعيد: يُنظِّم مُحاضر جامعي مواعيد لأربعةٍ من طلبته المُتوقَّع تخرُّجهم، في الساعة المُخصَّصة لعمله المكتبي كل يوم خميس. وبحسب خبرته،

فإنَّ عدد مَنْ يتأخَّرون عن موعد الساعة المكتبية من هؤلاء الطلبة يُمكِن تمثيله بمتغير عشوائي X، وإنَّ التوزيع الاحتمالي لهذا المتغير العشوائي هو

كما في الجدول الآتي:

أجد احتمال تأخُّر اثنين من هؤلاء الطلبة - على الأقل- عن موعد الساعة المكتبية يوم الخميس.

الحل : 

$$\begin{gathered} 0.4+0.25+4𝑘+2𝑘+𝑘=1 \\ 7𝑘+0.65=1 \\ 7𝑘=0.35 \\ \mathbf{𝑘}\mathbf{=}\mathbf{0}\mathbf{.}\mathbf{05} \end{gathered}$$

احتمال تأخُّر اثنين من هؤلاء الطلبة على الأقل =   $P (x \ge 2)$ 

$$\begin{gathered} P (x \ge 2) = P (x = 2) + P (x = 3) + P (x = 4) \\ = 0.2 + 0.1 + 0.05 \\ \mathbf{=}\mathbf{ }\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35} \end{gathered}$$   

                                                                                                                                                    

---

 

11) تحدٍّ : أجد قيمة k إذا كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي:

                                                                                                                                                                                                         {(1, 0.1x), (2, 0.1x), (3, 0.1x), (4, k)}

  الحل :                                                                                                                                                                                                                                         $$\begin{gathered} 0.1 \times 1 + 0.1 \times 2 + 0.1 \times 3 + k = 1 \\ 0.1 + 0.2 + 0.3 + k = 1 \\ 0.6 + k = 1 \\ \mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{4} \end{gathered}$$        

---

                                              

 

12) تحدٍّ : أجد المنوال للتوزيع الاحتمالي إذا كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي:

               

 الحل : 

أجد قيمة a

$$\begin{gathered} 0.1 + a + 0.3 + a + 0.1 = 1 \\ 2a + 0.5 = 1 \\ 2a = 0.5 \\ \mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{25} \end{gathered}$$

المنوال هو قيمة المتغير العشوائي الذي يأخذ الاحتمال الأكبر ، والاحتمال الأكبر في التوزيع الاحتمالي هنا يساوي 0.3 ، وهذا الاحتمال يقابل قيمة المتغير العشوائي 2 ؛ لذا المنوال للتوزيع الاحتمالي هو  2 

 

---

13) أكتب: أيُّ طرائق التعبير عن التوزيع الاحتمالي أفضل؟ أُبرِّر إجابتي.

يعتمد على اختيار الطالب . 

---

 

أسئلة كتاب التمارين 

إذا دُوِّر مُؤشِّرا القرصين عشوائيًّا في الشكل المجاور، وتوقَّف كل مُؤشِّر عند أحد الأعداد، ودلَّ المتغير العشوائي X على مجموع العددين، فأجد كلًّ ممّا يأتي: 1) التوزيع الاحتمالي في صورة جدول. 2) التوزيع الاحتمالي في صورة تمثيل بياني.

 

 

 

 

 

 

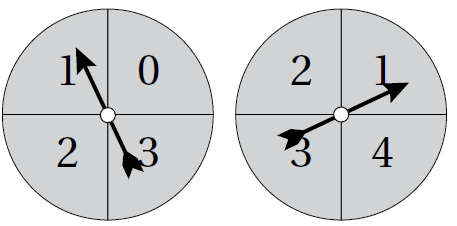 الحل : 

المجاميع الممكنة (قيم x ) هي : 1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 

عدد عناصر فضاء العينة :   Ω  =  16

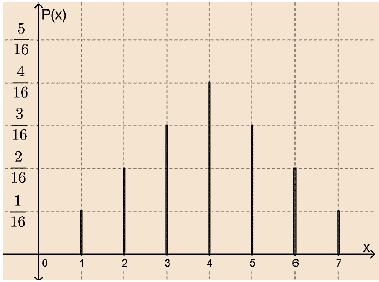
1) التوزيع الاحتمالي في صورة جدول.

7	6	5	4	3	2	1	x
$\frac{1}{16}$	$\frac{2}{16}$	$\frac{3}{16}$	$\frac{4}{16}$	$\frac{3}{16}$	$\frac{2}{16}$	$\frac{1}{16}$	P(x)

 

 

 

2) التوزيع الاحتمالي في صورة تمثيل بياني.

---

 

إذا دُوِّر المُؤشِّران السابقان عشوائيًّا، ودلَّ المتغير العشوائي X على حاصل ضرب العددين، فأجد كلًّ ممّا يأتي:
3) التوزيع الاحتمالي في صورة جدول.

4) التوزيع الاحتمالي في صورة تمثيل بياني.

 الحل : 

نواتج الضرب الممكنة (قيم x ) هي : 0 ، 1 ، 2 ، 3 ، 4 ، 6 ، 8 ، 9 ، 12

عدد عناصر فضاء العينة :   Ω  =  16

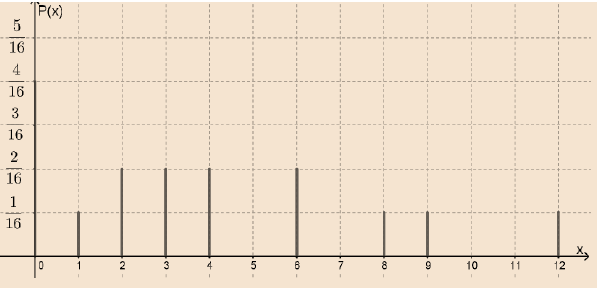
3) التوزيع الاحتمالي في صورة جدول.

12	9	8	6	4	3	2	1	0	x
$\frac{1}{16}$	$\frac{1}{16}$	$\frac{1}{16}$	$\frac{2}{16}$	$\frac{2}{16}$	$\frac{2}{16}$	$\frac{2}{16}$	$\frac{1}{16}$	$\frac{4}{16}$	P(x)

 

 

 

4) التوزيع الاحتمالي في صورة تمثيل بياني.

---

في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X كما في الجدول الآتي :

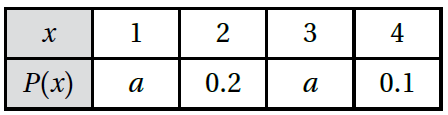
5) أجد قيمة a. 

6) أجد  $P (x = 3)$

7) أجد $P (2\le x < 4)$ 

8) أجد $P (1\le x < 2)$

الحل : 

5) أجد قيمة a. 

$$\begin{gathered} a + 0.2 + a + 0.1 = 1 \\ 2a + 0.3 = 1 \\ 2a = 0.7 \\ \mathit{a}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35} \end{gathered}$$

 

---

6) أجد $P (x = 3)$

$P (x = 3) =\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35}$

 

---

7) أجد $P (2\le x < 4)$

$$\begin{gathered} P (2\le x < 4) =P(x=2) + P(x = 3) \\ = 0.2 + 0.35 \\ \mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{55} \end{gathered}$$

---

8) أجد $P (1\le x < 2)$

$$\begin{gathered} P (1\le x < 2) \\ = P(x = 1) =\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{35} \end{gathered}$$

---

 

في تجربة عشوائية، كان التوزيع الاحتمالي للمتغير العشوائي X مُعرَّفًا على النحو الآتي:

                                                                                                                                                                                                                                               {(0, k), (1, 2k), (2, 2k)}

9) أجد قيمة K. 

10) أُنشِئ جدول التوزيع الاحتمالي.

11)  أجد $P (x\le 1)$

الحل :

9) أجد قيمة K. 

$$\begin{gathered} k + 2k + 2k = 1 \\ 5k = 1 \\ \mathit{k}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{2} \end{gathered}$$ 

 

---

10) أُنشِئ جدول التوزيع الاحتمالي.

2	1	0	x
0.4	0.4	0.2	P(x)

 

 

 

---

11)  أجد $P (x\le 1)$

$$\begin{gathered} P (x\le 1) = P(x=0) + P(x=1) \\ = 0.2 + 0.4 \\ \mathbf{=}\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{6} \end{gathered}$$

---

 

12) في تجربة سحب كرتين عشوائيًّا على التوالي من دون إرجاع من صندوق يحوي 4 كرات حمراء مرقمة من 1 إلى 4 ، و 5 كرات خضراء مرقمة من 1 إلى

5، جميعها مُتماثِلة، إذا دلَّ المتغير العشوائي X على عدد الكرات الحمراء في السحبة، فأُنشِئ جدول التوزيع الاحتمالي للمتغير العشوائي X

الحل : 

قيم المتغير العشوائي x  ، هي : 0 ، 1 ، 2 

                  $P(x=0) = \frac{5}{9}\times \frac{4}{8} =\frac{20}{72}=\mathbf{ }\frac{\mathbf{5}}{\mathbf{18}}$            

$P(x=1) = \frac{5}{9}\times \frac{4}{8} +\frac{4}{9}\times \frac{5}{8}=\frac{40}{72}=\mathbf{ }\frac{\mathbf{10}}{\mathbf{18}}$ 

                     $P(x=2) = \frac{4}{9}\times \frac{3}{8} =\frac{12}{72}=\mathbf{ }\frac{\mathbf{3}}{\mathbf{18}}$    

جدول التوزيع الاحتمالي للمتغير العشوائي X

2	1	0	x
$\mathbf{ }\frac{3}{18}$	$\mathbf{ }\frac{10}{18}$	$\mathbf{ }\frac{5}{18}$	P(x)