حلول أسئلة أتحقق من فهمي
دوَّرَ ليثٌ مؤشرَ القرصِ المجاورِ 10 مرّاتٍ، فَكانَتِ النتائجُ كَما في الجدولِ الآتي:
| أخضر | أصفر | أحمر | اللون |  |
| 3 | 5 | 2 | التكرار |
3) أَجِدُ الاحتمالَ التجريبيَّ لِتوقّفِ المؤشرِ عندَ اللّونِ الأخضرِ.
4) أَجِدُ الاحتمالَ التجريبيَّ لِتوقّفِ المؤشرِ عندَ اللّونِ الأصفرِ.
يحتوي قرصٌ دوّارٌ أربعةَ أقسامٍ مرقمةً مِنْ 1 إلى 4، وَعندَ تسجيلِ الرقمِ الّذي يستقرُّ عندَهُ المؤشرُ كانَتِ النتائجُ كَما في الجدولِ المجاورِ. هَلِ القرصُ مقسمٌ إلى أقسامٍ متساويةٍ؟ أبرّرُ إجابتي.
| 4 | 3 | 2 | 1 | الرقم |
| 11 | 9 | 10 | 10 | التكرار |
الْخُطْوَةُ 1: أَجِدُ الاحتمالَ النظريَّ لِظهورِ كلِّ رقْمٍ على القرص:
الْخُطْوَةُ2: أَجِدُ الاحتمالَ التجريبي لِظهورِ كلِّ رقْمٍ على القرص:
قيم الاحتمال النظري قريبة جدا من قيم الاحتمال التجريبي لذا فإن القرص مقسم إلى أقسام متساوية.
رُصِدَتْ عددُ الأيامِ الماطرةِ في آخرِ 12 يومًا مِنْ شهرِ آذارَ فَوُجِدَ أَنَّها يومان. إذا استمرَّ هَطلُ الأمطارِ بِالمعدلِ نفسِهِ، فَكَمْ يومًا مِنَ المتوقَّعِ أَنْ يكونَ ماطرًا في شهرِ نَيسانَ؟
الْخُطْوَةُ 1: أَجِدُ الاحتمالَ التجريبيَّ:
الْخُطْوَةُ 2: أضربُ الاحتمالَ التجريبيَّ لِلأيام الماطرة في عدد ايام الشهر :
عدد الأيام الماطرة المتوقعة هي 5 أيام
حلول أسئلة أتدرب وأحل المسائل
يبيّنُ الجدولُ المجاورُ نتائجَ رَميِ قطعةٍ نقديةٍ 100 مرةٍ وَتسجيلَ الوجهِ العُلويِّ. أَجِدُ الاحتمالَ التجريبيَّ لِ:
| 37 | صورة |
| 63 | كتابة |
1) ظهورِ صورةٍ.
2) ظهورِ كتابةٍ.
لدى كلٍّ مِنْ هاشمٍ وَميسونَ قرصٌ دوّارٌ يحتوي أربعةَ أقسامٍ مرقَّمةً مِنْ 1 إلى 4، أدارَ كلٌّ مِنْهُما قرصَهُ وَسجّلَ الرقْمَ الّذي استقرَّ عندَهُ وسجّلَ النتائجَ في الجدولَينِ الآتيَينِ:
|
|
||||||||||||||||||||||||||||||
3) كَمْ مرَّةً أدارَ كلٌّ مِنْهُما قرصَهُ؟
مجموع تكرارات التجربة لدى هاشم : 50 مرة
مجموع تكرارات التجربة لدى ميسون: 100 مرة
4) أَجِدُ الاحتمالَ التجريبيَّ لِتوقّفِ المؤشرِ عندَ كلِّ رقْمٍ على القرصِ الدوّارِ.
قرص ميسون:
قرص هاشم:
5) أيٌّ مِنْهُما قد يكونُ قرصُهُ مقسمًا إلى أقسامٍ متساويةٍ؟ أبرّرُ إجابتي.
كلاهما لأن نتائجهما قريبة من الاحتمال النظري والذي يساوي 0.25
يبيّنُ الجدولُ المجاورُ أنواعَ المركباتِ وَأعدادَها الّتي رصدَتْها كاميرا مراقبةٍ عندَ مرورِها في أحدِ الشوارعِ خلالَ المدةِ الزمنيةِ من 5pm وحتى 6pm أستعملُ الجدولَ لَِتجِدَ الاحتمالَ التجريبيَّ لِ:
| شاحنة | دراجة | سيارة |
| 8 | 8 | 19 |
6) مرورِ سيّارةٍ أمامَ الكاميرا.
الاحتمالَ التجريبيَّ
7) مرورِ درّاجةٍ أمامَ الكاميرا.
الاحتمالَ التجريبيَّ
8) مرورِ شاحنةٍ أمامَ الكاميرا.
الاحتمالَ التجريبيَّ
9) بيضٌ: فحصَ تاجرٌ 20 طبقَ بيضٍ فَوجدَ أَنَّ 3 أطباقٍ تحوي بيضًا مكسورًا. كَمْ طبقَ بيضٍ مِنَ المتوقَّعِ وجودُ بيضٍ مكسورٍ فيهِ مِنْ 1000 طبقٍ؟
الْخُطْوَةُ 1: أَجِدُ الاحتمالَ التجريبيَّ:
الْخُطْوَةُ 2: أضربُ الاحتمالَ التجريبيَّ للأطباق المكسورة في عدد الأطباق :
عدد الأطباق المتوقع وجود بيض مكسور فيها 150 طبق
يبيّنُ التمثيلُ بِالأعمدةِ المجاورُ نتائجَ تجربةِ إلقاءِ حجرِ نردٍ وَتسجيلِ الرقْمِ الظاهرِ على وجهِهِ العُلويِّ، أَجِدُ الاحتمالَ التجريبيَّ لِ:
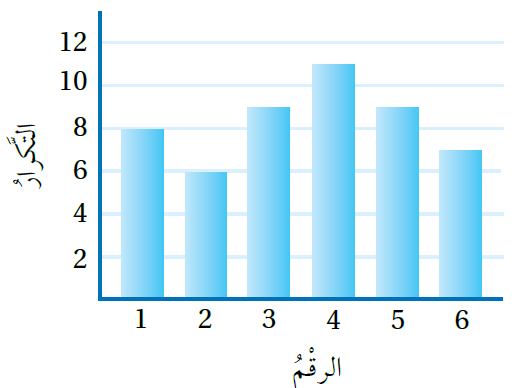
نجد عدد مرات القاء حجر النرد
10) ظهورِ الرقْمِ 6
11) عدمِ ظهورِ الرقْمِ 1
12) ظهورِ رقْمٍ أقلَّ مِنْ 3
13) ظهورِ الرقْمَينِ 2 أَوْ 4
تبريرٌ: سجّلَ يوسفُ عددَ مرّاتِ فوزِ وَخسارةِ وَتعادُلِ فريقِ كرةِ السلةِ الّذي يشجعُهُ في موسمٍ واحدٍ في الجدولِ المجاورِ:
| خسارة | تعادل | فوز |
| 19 | 25 | 36 |
نجد عدد المباريات
14) أَجِدُ الاحتمالَ التجريبيَّ لِفوزِ الفريقِ.
15) معتمدًا على نتائجِ الاحتمالِ التجريبيِّ، هَلْ مِنَ المتوقَّعِ فوزُ الفريقِ في المباراةِ القادمةِ؟ أبرّرُ إجابتي.
الاحتمال النظري للفوز
الاحتمال التجريبي للفوز
الاحتمال التجريبي للفوز اكبر من الاحتمال النظري مما يعني انه من المتوقع فوز الفريق بالمباراة القادمة
تبريرٌ: قرصٌ دوّارٌ يحتوي أربعةَ أقسامٍ لِكُلٍّ مِنْها لونٌ مختلِفٌ. بيبّنُ الجدولُ المجاورُ نتائجَ تجربةِ تدويرِ مؤشرِهِ 200 مرةٍ:
| أسود | أزرق | زهري | أحمر | |
| 72 | 36 | التكرار | ||
| 0.36 | 0.29 | الإحتمال التجريبي |
16) أكملُ الجدولَ.
نجد الاحتمال التجريبي للون الأحمر
نجد تكرار اللون الزهري من الاحتمال التجريبي المعطى
نجد تكرار اللون الأسود ، ثم نجد الاحتمال التجريبي
| أسود | أزرق | زهري | أحمر | |
| 34 | 72 | 58 | 36 | التكرار |
| 0.17 | 0.36 | 0.29 | 0.18 | الإحتمال التجريبي |
17) أيُّ قسمَينِ في القرصِ مِنَ المتوقعِ أَنْ يكونَ لَهُما المقاسُ نفسُهُ؟ أبرّرُ إجابتي.
الأحمر والأسود ، الاحتمال التجريبي لهما متقارب
18) أكتبُُ كيفَ أَجِدُ الاحتمالَ التجريبيَّ لِحادثٍ ما؟
من خلال قسمة عدد مرات وقوع الحادث على عدد مرات اجراء التجربة
حلول أسئلة كتاب التمارين
يبيّنُ التمثيلُ بِالأعمدةِ المجاورُ نتائجَ تدويرِ مؤشرِ القرصِ المجاورِ 200 مرةٍ وَتسجيلِ الرقْمِ الّذي يستقرُّ عندَهُ المؤشرُ، أَجِدُ الاحتمالَ التجريبيَّ لِ :
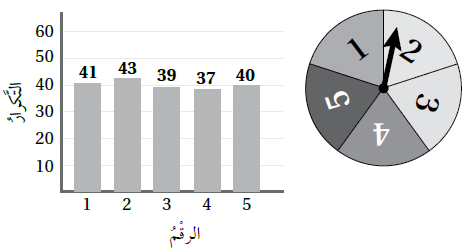
1) توقُّفِ المؤشرِ عندَ الرقْمِ 3
2) توقّفِ المؤشرِ عندَ رقْمٍ أكبرَ مِنْ 4
3) توقّفِ المؤشرِ عندَ عددٍ غيرِ أوّليٍّ.
في تجربةِ إلقاءِ حجرِ نردٍ 75 مرةً وَتسجيلِ الرقْمِ الظاهرِ على الوجهِ العُلويِّ ظهرَ العددُ (6)25 مرةً:
4) أَجِدُ الاحتمالَ التجريبيَّ لِظهورِ العددِ 6
5) هلْ حجرُ النردِ المستعملُ في التجربةِ عادلٌ أَمْ لا؟ أبرّرُ إجابتي.
الاحتمال النظري لظهور العدد 6 هو ، اذن الحجر غير عادل لأن الاحتمال النظري بعيد عن التجريبي
مطاعمُ: يقدّمُ مطعمٌ عرضًا لِلزبائنِ بِاختيارِ طبقٍ إضافيٍّ مَعَ وجباتِهِمْ مِنْ بَينِ ثلاثةِ أطباقٍ: بطاطا، أَوْ أَرُزٍّ، أَوْ معكرونةٍ، وَيبيّنُ الجدولُ المجاورُ طلباتِ الزبائنِ في أحدِ الأيامِ.
| الطلبُ الإضافيُّ | العددُ |
| أَرُزٍّ | 29 |
| بطاطا | 13 |
| معكرونةٍ | 1 |
6) أَجِدُ الاحتمالَ التجريبيَّ لِاختيارِ زبونٍ طبقَ البطاطا.
7) إذا ارتادَ المطعمَ في اليومِ التالي 80 شخصًا، فَكَمْ زبونًا مِنَ المتوقَّعِ أَنْ يختارَ طبقَ الأرُزِّ.
نجد الاحتمال التجريبي للارز ونضربه بعدد الزبائن المتوقع
تقريباً 54 شخص يتوقع أن يطلبو طبق الأرز
صمّمَتْ سارةُ القرصَ الدوّارَ المجاورَ، وَدوّرَتِ المؤشرَ 40 مرةً، ثُمَّ رصدَتِ النتائجَ الّتي حصلَتْ عليها في الجدولِ المجاور:
 |
||||||
|
8) أَجِدُ الاحتمالَ التجريبيَّ لِتوقّفِ المؤشرِ عندَ اللونِ الأزرقِ.
9) هلِ القرصُ الّذي صممَتْهُ سارةُ عادلٌ أَمْ لا؟
لا ، لأن المساحة الزرقاء أكبر بكثير من الأحمر وهذا انعكس بالتجربة على الفجوة الواضحة بين عدد التكرارات للونين