الدرس الرابع: الاشتقاق الضمني والمُعدًلات المرتبطة
سنتعرف في درس الاشتقاق الضمني والمُعدًلات المرتبطة إلى:
- العلاقة الضمنية.
- اشتقاق العلاقة الضمنية.
- معادلة المماس لمنحنى علاقة ضمنية.
- المعدلات المرتبطة.
أولًا: الاشتقاق الضمني
تنقسم العلاقات إلى قسمين
- علاقات صريحة
- علاقات ضمنية
---العلاقة الصريحة: هي العلاقة التي تكون على الصورة ؛ أي أن بدلالة ، ومن الأمثلة عليها:
وتعلمت سابقًا طرق اشتقاقها.
--- العلاقة الضمنية: هي علاقة لا يكون فيها بدلالة ؛ أي ليست على الصورة ، ومن الأمثلة عليها:
وسوف نتعلم في هذا الدرس كيفية اشتقاق العلاقة الضمنية
طريقة اشتقاق العلاقة الضمنية
- أشتق طرفي المعادلة بالنسبة إلى ، مراعيًا استعمال قاعدة السلسلة عند اشتقاق حدود تتضمن المتغير .
- أنقل جميع الحدود التي تحوي إلى طرف المعادلة الأيسر ، ثم أنقل الحدود الأُخرى إلى طرف المعادلة الأيمن.
- أُخرج عاملاً مشتركًا من حدود طرف المعادلة الأيسر.
- أحل المعادلة بإيجاد .
مثال 1: إذا كان: ، أجد
الحل:
| المعادلة المعطاة | |
| نشتق طرفي المعادلة بالنسبة للمتغير | |
| باستخدام قاعدتا مشتقة المجموع ومشتقة الثابت | |
| باستخدام قاعدتا مشتقة اقتران القوة ومشتقة السلسلة | |
| بحل المعادلة | |
| بالتبسيط |
مثال 2: إذا كان: ، أجد
الحل:
| المعادلة المعطاة | |
| باشتقاق طرفي المعادلة بالنسبة للمتغير | |
| باستخدام قاعدتا مشتقة المجموع ومشتقة الثابت | |
| باستخدام قواعد مشتقة القوة ومشتقة الضرب ومشتقة السلسلة | |
| بالتبسيط |
مثال 3: إذا كان: ، أجد عند النقطة .
الحل:
| المعادلة المعطاة | |
| باشتقاق المعادلة بالنسبة للمتغير | |
| باستخدام قاعدتا مشتقة الطرح ومشتقة الثابت | |
| باستخدام قواعد مشتقة القوة ومشتقة الضرب ومشتقة السلسلة | |
| بالتبسيط | |
| بتعويض |
إذًا، عند النقطة هي:
مثال 4: إذا كان: ، أجد
الحل:
| المعادلة المعطاة | |
| باشتقاق طرفي المعادلة بالنسبة للمتغير | |
| باستخدام قاعدتا مشتقة القوة ومشتقة السلسلة | |
| بالتبسيط |
مثال 5: إذا كان: ، أجد
الحل:
| المعادلة المعطاة | |
| باشتقاق طرفي المعادلة بالنسبة للمتغير | |
| باستخدام قاعدة مشتقة الضرب | |
| باستخدام قواعد مشتقة القوة ومشتقة السلسلة ومشتقة |
مثال 6: إذا كان: ، أجد
الحل:
| المعادلة المعطاة | |
| باشتقاق طرفي المعادلة | |
| باستخدام قاعدة مشتقة المجموع | |
| باستخدام قاعدة مشتقة الضرب | |
| باستخدام قاعدتا مشتقة القوة ومشتقة | |
| بالتبسيط |
مثال 7: ، أجد
الحل
| المعادلة المعطاة | |
| نشتق 'طرفي المعادلة بالنسبة للمتغير | |
| باستخدام قاعدة مشتقة المجموع | |
| باستخدام مشتقة القوة ومشتقة | |
| بالتبسيط |
مثال 8: إذا كان: ، أجد .
الحل:
| المعادلة المعطاة | |
| اشتق طرفي المعادلة بالنسبة للمتغير | |
| استخدم قاعدتا مشتقة المجموع ومشتقة الثابت | |
| استخدم قاعدتا مشتقة القوة ومشتقة السلسلة | |
| بالتبسيط |
مثال 9: إذا كان: ، أجد عند النقطة
الحل:
| المعادلة المعطاة | |
| باشتقاق طرفي المعادلة | |
| باستخدام قاعدة مشتقة المجموع | |
| باستخدام قواعد مشتقة القوة ، ومشتقة السلسلة ومشتقة الثابت، ومشتقة | |
| بالتبسيط | |
| بتعويض |
إذًا، عند النقطة هي:
أتحقق من فهمي
- إذا كان: ، أجد . الإجابة:
- إذا كان: ، أجد . الإجابة:
- إذا كان: ، أجد عند النقطة . الإجابة:
ثانيًا: معادلة المماس لمنحنى علاقة ضمنية
يمكن إيجاد معادلة المماس لمنحنى علاقة ضمنية عند النقطة بإيجاد ميله ، ثم التعويض في الصورة العامة لمعادلة المماس:
مثال 1: أجد ميل المماس لمنحنى العلاقة: عند النقطة .
الحل:
ميل المماس لمنحنى العلاقة يساوي المشتقة عند النقطة
| المعادلة المعطاة | |
| نشتق طرفي المعادلة | |
| استخدم قواعد مشتقة الطرح ومشتقة القوة وشتقة السلسلة | |
| بالتبسيط | |
| بتعويض |
إذًا، ميل المماس لمنحنى العلاقة عند النقطة هو:
مثال 2: أجد ميل المماس لمنحنى العلاقة: عند النقطة
الحل:
ميل المماس لمنحنى العلاقة يساوي المشتقة عند النقطة
| المعادلة المعطاة | |
| نشتق طرفي المعادلة للمتغير | |
| باستخدام قاعدتا مشتقة المجموع ومشتقة الطرح | |
| باستخدام قواعد مشتقة القوة ومشتقة الضرب ومشتقة الثابت | |
| نعوض |
إذًا، ميل المماس لمنحنى العلاقة عند النقطة هو:
مثال 3: أجد معادلة المماس لمنحنى العلاقة: عند النقطة .
الحل:
الخطوة 1: أجد ميل منحنى العلاقة عند النقطة.
| المعادلة المعطاة | |
| بإشتقاق طرفي المعادلة | |
| باستخدام قاعدتا مشتقة المجموع ومشتقة الثابت | |
| باستخدام قاعدتا مشتقة القوة ومشتقة السلسلة | |
| بالتبسيط | |
| بتعويض |
إذًا، ميل المماس لمنحنى العلاقة هو:
الخطوة 2: أجد معادلة المماس عند النقطة .
| معادلة المماس عند النقطة | |
| بتعويض | |
| بالتبسيط من خلال الضرب وإضافة لطرفي المعادلة والجمع |
إذًا، معادلة المماس لمنحنى العلاقة عند النقطة هي:
مثال4: أجد معادلة المماس لمنحنى العلاقة: عند النقطة .
الحل:
الخطوة 1: أجد ميل المماس عند النقطة
| المعادلة المعطاة | |
| نشتق طرفي المعادلة | |
| باستخدام قاعدتا مشتقة المجموع ومشتقة الثابت | |
| باستخدام قاعدتا مشتقة الضرب ومشتقة القوة ومشتقة السلسلة | |
| بالتبسيط | |
| بتعويض |
إذًا، ميل المماس لمنحنى العلاقة عند النقطة هو:
الخطوة 2: أجد معادلة المماس عند النقطة
| معادلة المماس | |
| بتعويض | |
| بالتبسيط |
إذًا، معادلة المماس لمنحنى العلاقة عند النقطة هي:
أتحقق من فهمي
1) أجد ميل المماس لمنحنى العلاقة: عند النقطة . الإجابة: ميل المماس هو:
2) أجد معادلة المماس لمنحنى العلاقة: عند النقطة . الإجابة: معادلة المماس هي:
ثالثًا: المُعدَلات المرتبطة بالزمن
هناك كثير من المسائل الحياتية يتطلب حلها إيجاد معدل التغير بالنسبة للزمن وتسمى معُدَلات مرتبطة بالزمن ومن الأمثلة عليها معدل تغير المساحة بالنسبة للزمن ، ومعدل تغير الحجم بالنسبة للزمن ومعدل تغير المسافة بالنسبة للزمن.
يكون معدل التغير موجباً إذا كان معدل التغير متزايدًا ، ويكون معدل التغير سالباً إذا كان معدل التغير متناقصًا.
ولحل المُعدَلات المرتبطة بالزمن نستخدم الاشتقاق الضمني بالنسبة للزمن وقاعدة السلسلة.
مثال 1: قرص دائري معدني يتمدد بالحرارة محافظًا على شكله بمعدل ، أجد معدل تغير طول نصف قطر القرص عندما يكون طوله . علمًا بأن العلاقة التي تربط مساحة الدائرة وطول نصف قطرها هي:
الحل:
الخطوة 1: أُحدد المعطيات والمطلوب
المعطيات:
المعادلة:
معدل التغير المعطى:
المطلوب: عندما
الخطوة 2: أشتق طرفي المعادلة بالنسبة للزمن ، ثم أُعوض
| المعادلة | |
| أشتق طرفي المعادلة بالنسبة ل | |
| أستخدم قاعدة السلسلة ومشتقة القوة | |
| أُعوض | |
| بالتبسيط |
إذًا، يزداد طول نصف قطر القرص بالنسبة للزمن بمقدار عندما يكون طوله
مثال 2: صفيحة معدنية مستطيلة الشكل تتمدد بانتظام بحيث يزداد طولها بمعدل ، ويزداد عرضها بمعدل ، وفي لحظة معينة كان طولها،وعرضها يساوي . أجد معدل التغير في مساحة الصفيحة المعدنية في تلك اللحظة. علمًا بأن العلاقة التي تربط بين مساحة المستطيل وطوله وعرضه هي: .
الحل: 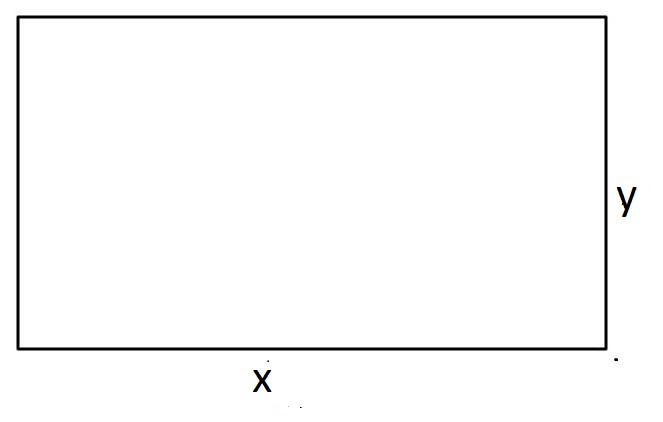
الخطوة 1: أُحدد المعطيات والمطلوب
المعطيات:
المعادلة:
معدل التغير المعطى:
المطلوب: عندما
الخطوة 2: أشتق طرفي المعادلة بالنسبة للزمن ، ثم أُعوض
| المعادلة | |
| أشتق طرفي المعادلة بالنسبة ل | |
| أستخدم قاعدتا مشتقة الضرب ومشتقة السلسلة | |
| أُعوض | |
| بالتبسيط |
إذًا، تزداد مساحة الصفيحة المعدنية بمقدار عندما عرضها وطولها
مثال 3: مكعب من الثلج يذوب محافظًا على شكله بمعدل ، جد معدل التناقص في طول ضلعه عندما يكون طول ضلعه .علمًا بأن العلاقة التي تربط بين حجم المكعب وطول ضلعه هي: .
الحل: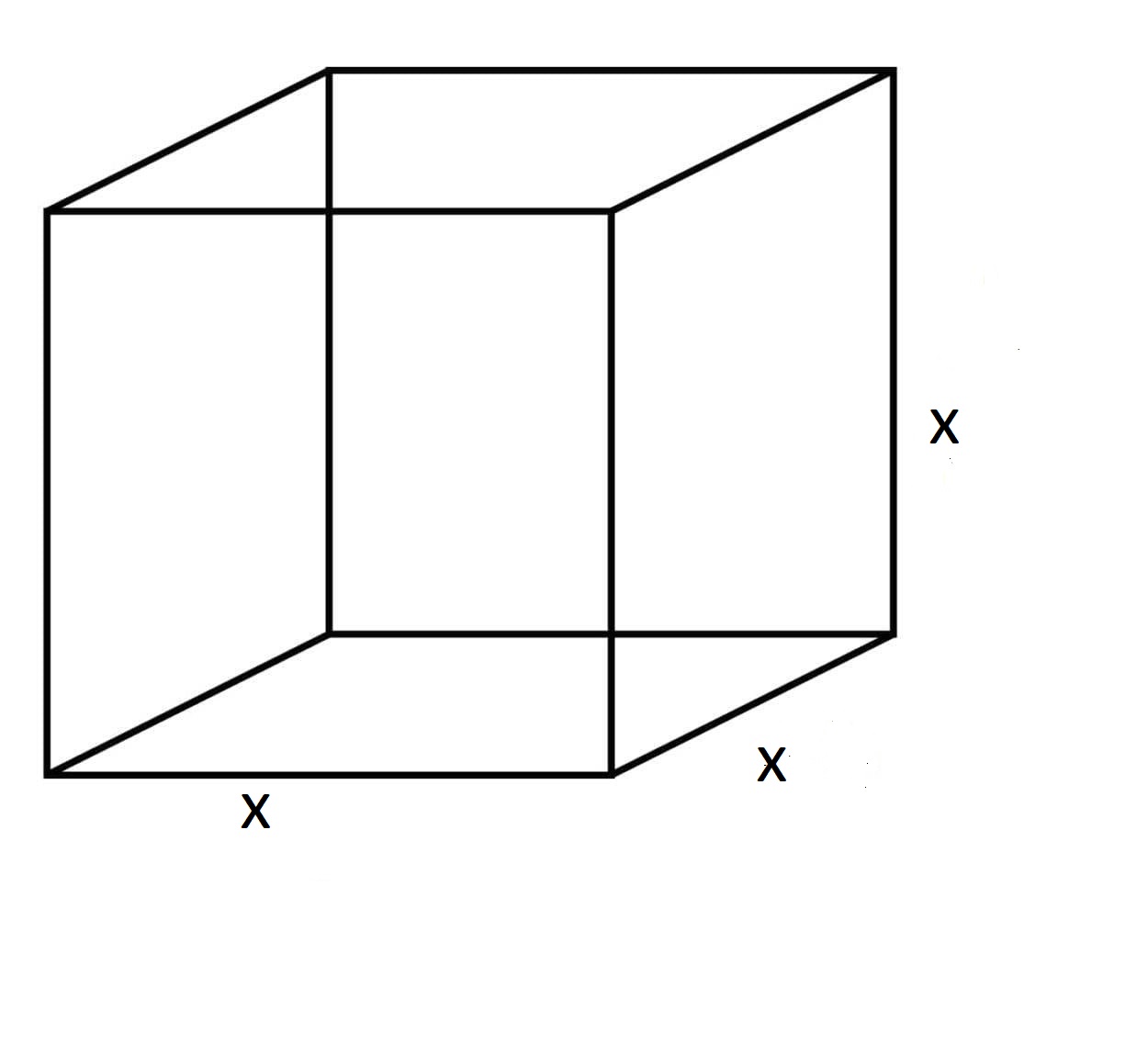
الخطوة 1: أُحدد المعطيات والمطلوب المعادلة
المعطيات:
المعادلة:
(المكعب يذوب، إذن أضع إشارة السالب ليدل على التناقص)
المطلوب:
عندما
الخطوة 2: أشتق طرفي المعادلة بالنسبة للزمن ، وأُعوض
| المعادلة | |
| أشتق طرفي المعادلة بالنسبة للمتغير | |
| أستخدم قاعدتا مشتقة القوة ومشتقة السلسلة | |
| أُعوض | |
| بالتبسيط |
إذًا، يتناقص طول ضلع المكعب بمقدار عندما طول ضلعه
مثال 4: بالون كروي يتزايد طول نصف قطره بمعدل ، أجد معدل تغير حجمه عندما يكون طول نصف قطره . علمًا بأن العلاقة التي تربط بين الحجم وطول نصف قطر البالون الكروي هي: .
الحل:
الخطوة 1: أحدد المعطيات والمطلوب
المعطيات:
المعادلة:
المطلوب:
، عندما
الخطوة 2: أشتق طرفي المعادلة بالنسبة للزمن ، وأُعوض
| المعادلة | |
| أشتق طرفي المعادلة بالنسبة للمتغير | |
| استخدام قاعدتا مشتقة السلسلة ومشتقة القوة | |
| أُعوض | |
| بالتبسيط |
إذًا، يزداد حجم البالون الكروي بمعدل عندما يكون طول نصف قطرها
أتحقق من فهمي
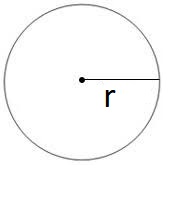
كرة من المعدن تتمدد بالحرارة مع المحافظة على شكلها ، فإذا كان حجمها يتزايد بمعدل ، أجد معدل التغير في طول نصف قطرها عندما يكون طول نصف قطرها
الإجابة: يزداد طول نصف قطر الكرة بمقدار عندما يكون طول نصف قطرها
_1662314562.jfif)