رياضيات 10 فصل ثاني

أتحقق من فهمي صفحة 64

اجد مشتقة كل اقتران مما ياتي: 

 

 

 

---

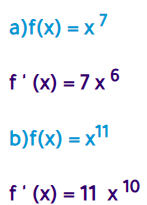
اتحقق من فهمي صفحة 65

احد متشقة  كل اقتران في ما ياتي: 

 

---

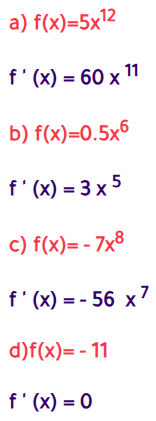
اتحقق من فهمي صفحة 66

اجد مشقة كل من الاقترانين الآتيين :

_________________________________________________________________________________________________________________________________________________________________________________________________________________-

 

 

اتحقق من فهمي صفحة 67

اذا كان f(x)= 5x² +25x - 9، فاستعمل المشتقة لايجاب كل مما ياتي: 

a) ميل منحنى f(x) عندما x= -2

f ' (x) = 10 x + 25 

ميل المنحنى عند  x= -2  هو مشتقة الاقتران عند تلك النقطة أي  f ' (-2) 

f ' ( -2 ) = -20 +25 = 5

b)قيمة x التي يكون عندها ميل منحنى الاقتران صفرا 

ميل المنحنى عند تلك القيم = مشتقة الاقتران عند تلك القيم = صفر 

f ' (x) = 10x +25 

0 = 10x +25 

10x = -25 

x = - 2.5 

---

اتحقق من فهمي صفحة 68

يمثل الاقتران d(t)=2.5 t² + 0.1t -0. 3 المسفة (بالمتر) التي يقطعها جسم متحرك، حيث t الزمن بالثانية . اجد سرعة الجسم وتسارعه عندما t=3.

v ( t) = d'(t) = 5 t + 0.1

a(t) = v '(t) = 5

v (3) = 15+ 0.1 = 15.1 

 a (3) = 5 

---

اتدرب واحل المسائل صفحة 68, 69

1) f(x)= -7

f ' (x) = 0

2) g(x)=3 x⁹

 

g ' (x) = 27 x⁸

3) r(x)= -5x²

 

r' (x) = -  10 x 

4) i(x)= x⁴ - 3x

 

i ' (x) = 4 x³ - 3

5) v(x)= x² + x + 1

 

v ' (x) = 2x +1 

6) t(x)= 6 - 2x + x²

 

t ' (x) = -2 + 2x 

 

---

اجد قيمة f' (-2) في كل مما ياتي: 

 

 

 

---

 

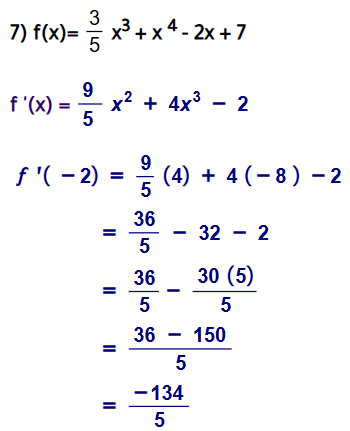
10) اجد النقطة التي يكون عندها ميل منحنى الاقتران f(x) = 2 x² - 10 هو 12

f' (x) = 4x 

ميل المنحنى = ميل المماس عند تلك النقطة = 12 

12 = 4 x

x = 3 

نعوض x = 3 في الاقتران f(x)  فتنتج النقطة 

( 3 , 8) 

---

 

يمثل الاقتران d(t)= t³ - 6t + 3 المسافة (بالمتر) التي يقطعها جسم متحرك، حيث t الزمن بالثانية : 

11) اجد الاقتران v(t) الذي يمثل سرعة الجسم في اي لحظة (t ثانية) 

v (t) = d'( t) = 3 t² - 6 

12) اجد سرعة الجسم عندما t = 3

v ( 3) = 3 (9) - 6 = 27 - 6 = 21 

13) اجد الزمن t عندما تكون  6m/s

6 = 3 t² - 6 

3 t² = 12 

t² = 4 

  t = -2   مرفوض

t = 2 

14) اجد الاقتران a(t) الذي يمثل تسارع الجسم، حيث t الزمن بالثانية 

a (t) = v'(t) = 6 t

15) اجد تسارع الجسم عندما t = 5

a ( t) = 6 (5) = 30

---

 

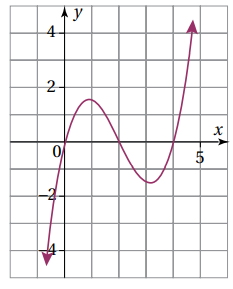
يمثل الشكل المجاور منحنى الاقتران f(x) = 0.5x ³ - 3 x² +  4x :

16) اجد f’(x) 

f '(x) = 1.5 x² - 6 x + 4

17) اجد ميل منحنى الاقتران عند نقاط تقاطعه مع محور  x

نقاط التقاطع هي  ( 0 , 0)  و ( 0 , 2 ) و ( 0 , 4) 

عند النقطة ( 0 , 0) 

 m = f' (0) = 0 - 0 +4 = 4

عند النقطة ( 0 , 2)

m = f' (2) = 6 - 12 +4 = -2

عند النقطة ( 0 , 4)

m = f' (4 ) = 24 - 24 + 4 = 4 

 

18) احدد على المنحنى النقطة التي يساوي عندما الميل 0.5 -

 

---

 

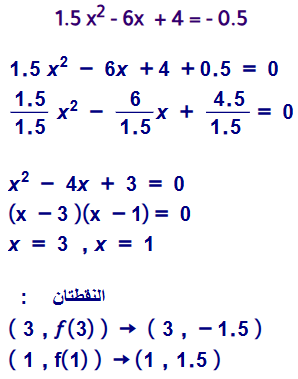
19) اجد معادلة مماس منحنى الاقتران f(x)= 3x³ + 2 عند النقطة التي يكون  احداثي x لها 1

f ' (x) = 9 x² 

m = f '(1) = 9 

* عندما  y = 5 , x = 1      

                      النقطة ( 5 ,1 )  تقع على المنحنى والمماس 

معادلة المماس 

 y - 5 = 9 ( x -1 ) 

y = 9x -9 +5 

y = 9x - 4 

---

 

تقع النقطة P (-2, b) على منحنى الاقتران g(x)= 3x³ - x² - 7x+ 4 : 

20)اجد قيمة b

بالتعويض المباشر 

g( -2 ) = b

3 ( -8) - 4 - 14 +4 =  b

b = -10

21) اجد قيمة x التي يكون عندما ميل منحنى الاقتران صفرا

g '(x) = 9x² - 2x - 7 

0 = 9x² -2 x - 7 

(  9x +7 ) ( x -1) = 0

$\mathit{x}\mathbf{=}\mathbf{-}\frac{\mathbf{7}}{\mathbf{9}}\mathbf{,}\mathit{x}\mathbf{=}\mathbf{1}$  

---

 

اذا كان قيمة الميل عندما x=2 لمنحنى المعادلة y= x³ - 2 a x، حيث a عدد ثابت، هي  12 -

22) اجد قيمة الثابت a

 

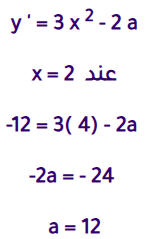
23) اجد قيمة ميل المنحنى عندما x = 4

y' = 3 x² - 24 

 عند  x  = 4 

y' = 3 (16) -24 = 24 

ميل المنحنى = 24

---

 

اجد f’(x) في كل مما ياتي: 

24) f(x)= 2x (x+1) 

f(x) = 2x² + 2x 

f '(x) = 4x + 2

25) f(x)=(x+2)(x+5)

f(x) = x² +2x +5x +10 = x² +7x +10

f '(x) = 2x +7 

26) f(x)=(x+3)(x-3)

f(x) = x² - 9 

f '(x) = 2x  

---

 

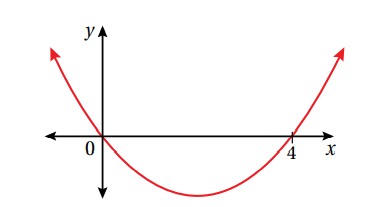
27) يبين الشكل المجاور التمثيل البياني للاقتران f(x)= k x (x - 4)،حيث k عدد حقيقي. اجد قيمة k اذا كان ميل المنحنى عند النقطة (4,0) هو 2

f (x) = k x² - 4k x 

f '(x) = 2 k x - 4 k 

عند النقطة ( 0 , 4) 

m = f ' (4)  = 2

2 = 2 k (4) - 4k 

2 = 8k - 4k 

2 = 4 k

$\mathit{k}\mathbf{=}\frac{\mathbf{1}}{\mathbf{2}}$

---

 

مهارات التفكير العليا 

28) تبرير: اثبت وجود نقطتين على منحنى الاقتران $f\left(x\right)=\frac{1}{3}{x}^3-5x+4$، تكون عندهما مشتقة الاقتران تساوي 4، ثم اجد احداثيي هاتين النقطتين، مبررا إجابتي 

f ' (x) = x² - 5 

 4 = x² - 5 

x² = 9 

x = 3   $\to$ y = -2  $\to$  ( 3 , -2 ) 

x = -3    $\to$y = 10   $\to$ ( -3 , 10) 

---

 

29) تحد: اجد قيم a,b اذا كان ميل منحنى الاقتران y= ax³ + bx² +5 عند النقطة (3-,2) هو صفرا 

y( 2) = -3

8a + 4b +5 = -3

8a +4b = -8 

2a +b = -2 

y ' = 3 a x² + 2bx 

12a + 4b = 0

$b=-2-2a$

بالتعويض بالمعادلة السابقة 

a = 1 

b = - 6 

---

 

30) تحدٍّ: أُطلِقَتْ قذيفةٌ منْ سطحِ الأرضِ رأسيًّا إلى الأعلى، فكانَ موقعُها بالنسبةِ لسطحِ الأرضِ ؟ بالمترِ بعدَ t ثانيةً منْ إطلاقِها $s\left(t\right)=-4.9t^2 +147t$. ما سرعةُ القذيفةِ عندَما يكونُ موقعُها 980m فوقَ سطحِ الأرضِ؟

---

 

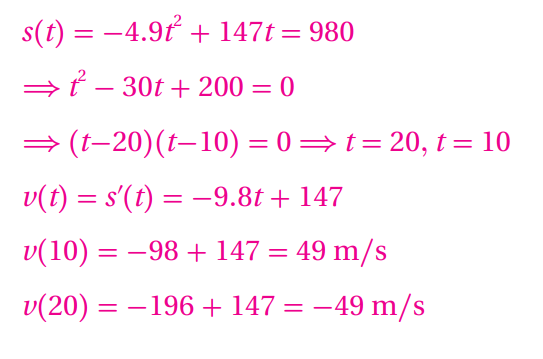
كتاب التمارين 

أجد مشتقة كل اقتران مما يأتي :

1.$\mathbf{ }\mathit{f}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{-}\frac{\mathbf{7}}{\mathbf{3}}$

f ' (x) = 0

2.$\mathbf{ }\mathit{f}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{8}}{\mathbf{5}}$

f ' (x) = 0

3. f(x) = -6x 

f ' (x) = -6

4. f(x) = 3.2x 

f ' (x) = 3.2 

5. f(x) = 3 x ⁴¹

f ' (x) = 123 x ⁴⁰ 

6. f(x) = - x ⁶⁴

f ' (x) = - 64 x ⁶³   

7. f(x) = x³ - 4 x ² + 3

f ' (x) = 3 x ² - 8x 

8. f(x) = 7x ³ +6 x ² - x 

f ' (x) = 21 x ² + 12 x - 1 

9. f(x) = (x +4)( x -2) 

f ' (x) = 2x +2 

10 . f(x) = ( x -5) ²

f ' (x) = 2x -10 

---

 

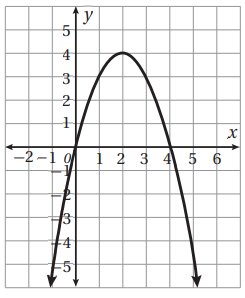
أستعمل  التمثيل البياني لمنحنى الاقتران f(x) = 4x - x ²  في الشكل المجاور للإجابة عن الأسئلة الآتية :

11.  أجد  f ' (x) 

f ' (x) = 4 -2x 

 

12. أجد ميل منحنى الاقتران عند نقطتي تقاطعه مع محور x

الميل عند ( 0 , 0) هو 4

الميل عند ( 0 , 4) هو 4 - 

 

13 . أحدد على المنحنى النقطة التي يكون عندا الميل 1

$4-2x=1\Rightarrow x=1.5\Rightarrow (1.5,3.75)$

 

14. أحدد على المنحنى النقطة التي يكون عندها الميل 2- 

(3 , 3) 

---

 

أجد قيمة (1-)' f  في كل مما يأتي :

15. f(x) = x ² - 3x +1

f ' (-1) = - 5

16. f(x) = x ³ - x ² - 2 

f ' (-1) = 5

---

 

17 . أجد النقطة التي يكون عندها ميل منحنى  f(x) = x ² - 5x +6  يساوي 9 - 

$(-2 , 20)$

---

 

إذا كان  f(x) = x ² + 5x  + 7  فاستعمل المشتقة لإيجاد كل مما يأتي :

 18. ميل منحنى f(x)  عندما  x = 2 

9

19. قيمة x  التي يكون ميل منحنى f(x)  يساوي 0

$-2.5$ 

 

20. تمثل العلاقة  d(t) = 2t³ -5 t ² +3t +4  المسافة ( بالمتر ) التي يقطعها جسم متحرك ، حيث t  الزمن بالثواني . 

أجد سرعة الجسم عندما  t = 2

7m / s

---

 

21.  إذا كان  f(x) = a x ⁿ + b  حيث b , a عددان حقيقيان و n  عدد صحيح غير سالب فأجد  f ' (x) 

 

f '(x) =na x ^{n -1}