رياضيات فصل أول

التوجيهي علمي

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

أجد قيمة الجذر الرئيس في كلّ مما يأتي بدلالة i :

$a) \sqrt{- 75} S o l u t i o n : \sqrt{- 75} = \sqrt{- 1 \times 25 \times 3} = \sqrt{- 1} \times \sqrt{25} \times \sqrt{3} = 5 i \sqrt{3}, \sqrt{- 1} = i$

$b) \sqrt{- 49} S o l u t i o n : \sqrt{- 49} = \sqrt{- 1 \times 49} = \sqrt{- 1} \times \sqrt{49} = 7 i, \sqrt{- 1} = i$

أجد ناتج كلّ مما يأتي في أبسط صورة مُفترضًا أنَّ $\sqrt{- 1} = i$ :

$a) \sqrt{- 27} \times \sqrt{- 48} S o l u t i o n : \sqrt{- 27} \times \sqrt{- 48} = \sqrt{- 1 \times 9 \times 3} \times \sqrt{- 1 \times 16 \times 3} = \sqrt{- 1} \times \sqrt{9} \times \sqrt{3} \times \sqrt{- 1} \times \sqrt{16} \times \sqrt{3} = 3 \sqrt{3} i \times 4 \times \sqrt{3} i, \sqrt{- 1} = i = 12 \times 3 i^{2}, i^{2} = - 1 = - 36$

$b) \sqrt{- 50} \times - 4 i S o l u t i o n : \sqrt{- 50} \times - 4 i = \sqrt{- 1 \times 25 \times 2} \times - 4 i = \sqrt{- 1} \times \sqrt{25} \times \sqrt{2} \times - 4 i = 5 \sqrt{2} i \times - 4 i, \sqrt{- 1} = i = - 20 \sqrt{2} i^{2}, i^{2} = - 1 = 20 \sqrt{2}$

$C) i^{2021} S o l u t i o n : i^{2021} = i^{2020} \times i^{1} = 1 \times i = i, i^{4 n} = 1 O r i^{2021} = {(i^{2})}^{1010} \times i = {(- 1)}^{1010} \times i = i$

أجد قيمة x وقيمة y الحقيقيتين اللتين تجعلان المعادلة: $x + 5 + (4 y - 9) i = 12 - 5 i$ صحيحة.

الحل:

بمساواة الجزء الحيقي الايمن بالايسر : $x + 5 = 12 \Rightarrow x = 7$

بمساواة الجزء التخيلي الايمن بالايسر : $4 y - 9 = - 5 4 y = 4 \Rightarrow y = 1$

أمثل العدد الُمركَّب ومرافقه بيانيًا في المستوى المُركَب في كل مما يأتي:

$a) z = 2 + 7 i$

$b) z = - 3 - 2 i$

$c) z = - 3 i$

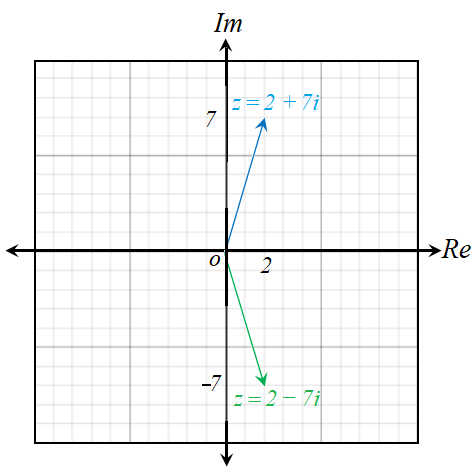
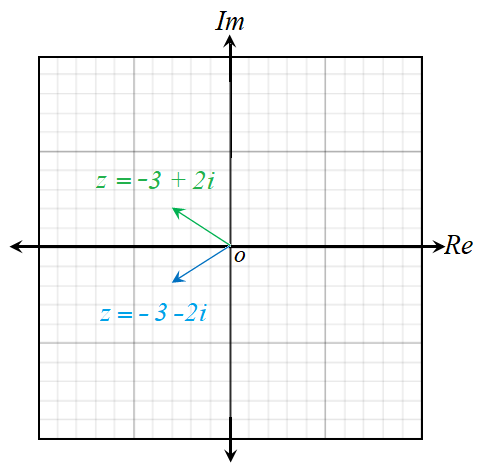
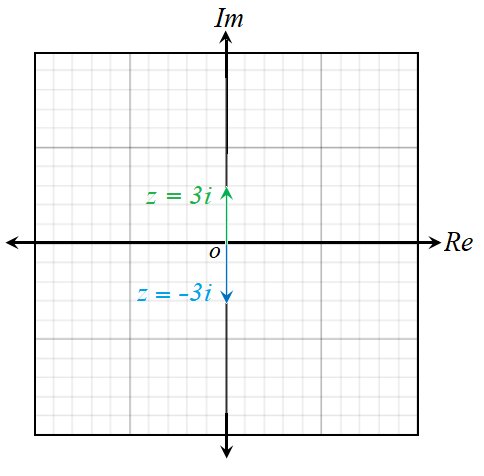
أجد مقياس كل عدد مُركَّبٍ مما يأتي :

$a) z = - 3 - 6 i \sqrt{2} S o l u t i o n : | z | = \sqrt{a^{2} + b^{2}} = \sqrt{{(- 3)}^{2} + {(- 6 \sqrt{2})}^{2}} = \sqrt{9 + 72} = \sqrt{81} = 9$

$b) z = - 2 i S o l u t i o n : | z | = \sqrt{a^{2} + b^{2}} = \sqrt{{(0)}^{2} + {(- 2)}^{2}} = \sqrt{4} = 2$

$c) z = 4 + \sqrt{- 20} S o l u t i o n : z = 4 + i \sqrt{20} | z | = \sqrt{a^{2} + b^{2}} = \sqrt{{(4)}^{2} + {(\sqrt{20})}^{2}} = \sqrt{16 + 20} = \sqrt{36} = 6$

أجد سعة كل من الأعداد المُركَبة الاتية مُقرّبَا إجابتي إلى أقرب منزلتين عشريتين:

$a) z = 8 + 2 i S o l u t i o n : A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{2}{8}) A r g (z) = t a n^{- 1} (\frac{1}{4}) = 0.24$

$b) z = - 5 + 12 i S o l u t i o n : A r g (z) = π - t a n^{- 1} (\frac{b}{a}) A r g (z) = π - t a n^{- 1} (\frac{12}{5}) = 1.97$

$c) z = - 2 - 3 i S o l u t i o n : A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - (π - t a n^{- 1} (\frac{3}{2})) = - 2.16$

$d) z = 8 - 8 i \sqrt{3} S o l u t i o n : A r g (z) = - t a n^{- 1} (\frac{b}{a}) A r g (z) = - t a n^{- 1} (\frac{8 \sqrt{3}}{8}) = - \frac{π}{3}$

أكتب العدد المُركَّب z في كل ممّا يأتي بالصورة المثلثية:

$a) | z | = 4 \sqrt{2}, A r g (z) = - \frac{3 π}{4} S o l u t i o n : z = r (c o s θ + i s i n θ) = 4 \sqrt{2} (c o s (- \frac{3 π}{4}) + i s i n (- \frac{3 π}{4}))$

$b) z = - 4 - 4 i S o l u t i o n : z = r (c o s θ + i s i n θ) r = \sqrt{{(4)}^{2} + {(4)}^{2}} = \sqrt{32} = 4 \sqrt{2} A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - π + t a n^{- 1} (\frac{4}{4}) A r g (z) = - π + \frac{π}{4} = - \frac{3 π}{4} z = r (c o s θ + i s i n θ) z = 4 \sqrt{2} (c o s (- \frac{3 π}{4}) + i s i n (- \frac{3 π}{4})) z = 4 \sqrt{2} (c o s (\frac{3 π}{4}) - i s i n (\frac{3 π}{4}))$

$c) z = 2 i S o l u t i o n : A r g (z) = t a n^{- 1} (\frac{2}{0}) = \frac{π}{2} A r g (z) = \frac{π}{2} z = r (c o s θ + i s i n θ) = 2 (c o s (\frac{π}{2}) + i s i n (\frac{π}{2}))$

أجد قيمة الجذر الرئيس في كلّ مما يأتي بدلالة i :

$1) \sqrt{- 19} S o l u t i o n : \sqrt{- 19} = \sqrt{- 1 \times 19} = \sqrt{- 1} \times \sqrt{19} = i \sqrt{19}, \sqrt{- 1} = i$

$2) \sqrt{- \frac{12}{25}} S o l u t i o n : \sqrt{- \frac{12}{25}} = \sqrt{- 1 \times \frac{12}{25}} = \sqrt{- 1} \times \frac{\sqrt{12}}{\sqrt{5}} = \frac{2 \sqrt{3}}{5} i, \sqrt{- 1} = i$

$3) \sqrt{- \frac{9}{32}} S o l u t i o n : \sqrt{- \frac{9}{32}} = \sqrt{- 1 \times \frac{9}{32}} = \sqrt{- 1} \times \frac{\sqrt{9}}{\sqrt{32}} = \frac{3}{4 \sqrt{2}} i, \sqrt{- 1} = i$

$4) \sqrt{- 53} S o l u t i o n : \sqrt{- 53} = \sqrt{- 1 \times 53} = \sqrt{- 1} \times \sqrt{53} = i \sqrt{53}, \sqrt{- 1} = i$

أجد ناتج كلّ مما يأتي في أبسط صورة مُفترضًا أنَّ $\sqrt{- 1} = i$

$5) i^{26} S o l u t i o n : i^{26} = {(i^{2})}^{13}, i^{2} = - 1 = {(- 1)}^{13} = - 1$

$6) i^{39} S o l u t i o n : i^{39} = i^{38} \times i = {(i^{2})}^{19} \times i, i^{2} = - 1 = {(- 1)}^{19} \times i = - 1 \times i = - i O r i^{39} = i^{(4 \times 9) + 3}, i^{4} = 1 i^{39} = {(i^{4})}^{9} \times i^{3}, i^{3} = - 1 i^{39} = {(1)}^{9} \times i^{3} = - i$

$7) i (2 i) (- 7 i) S o l u t i o n : i (2 i) (- 7 i) = - 14 i^{3}, i^{2} = - 1 = - 14 i^{2} \times i = - 14 (- 1) \times i = 14 i$

$8) \sqrt{- 6} \times \sqrt{- 6} S o l u t i o n : \sqrt{- 6} \times \sqrt{- 6} = {(\sqrt{- 1 \times 6})}^{2}, \sqrt{- 1} = i = {(\sqrt{- 1} \times \sqrt{6})}^{2} = {(i \times \sqrt{6})}^{2} = i^{2} \times 6 = - 6, i^{2} = - 1$

$9) \sqrt{- 4} \times \sqrt{- 8} S o l u t i o n : \sqrt{- 4} \times \sqrt{- 8} = \sqrt{- 1 \times 4} \times \sqrt{- 1 \times 8}, \sqrt{- 1} = i = \sqrt{- 1} \times \sqrt{4} \times \sqrt{- 1} \times \sqrt{8} = 2 i \times 2 i \sqrt{2} = i^{2} \times 4 \sqrt{2} = - 4 \sqrt{2}, i^{2} = - 1$

$10) 2 i \times \sqrt{- 9} S o l u t i o n : 2 i \times \sqrt{- 9} = 2 i \times \sqrt{- 1 \times 9}, \sqrt{- 1} = i = 2 i \times \sqrt{- 1} \times \sqrt{9} = 2 i \times 3 i = 6 i^{2} = - 6, i^{2} = - 1$

أكتب كلّ مما يأتي من الأعداد المركبة بالصورة القياسية:

$11) \frac{2 + \sqrt{- 4}}{2} S o l u t i o n : \frac{2 + \sqrt{- 4}}{2} = \frac{2 + \sqrt{- 1 \times 4}}{2}, \sqrt{- 1} = i = \frac{2 + 2 i}{2} = 1 + i$

$12) \frac{8 + \sqrt{- 16}}{2} S o l u t i o n : \frac{8 + \sqrt{- 16}}{2} = \frac{8 + \sqrt{- 1 \times 16}}{2}, \sqrt{- 1} = i = \frac{8 + 4 i}{2} = 4 + 2 i$

$13) \frac{10 - \sqrt{- 50}}{5} S o l u t i o n : \frac{10 - \sqrt{- 50}}{5} = \frac{10 - \sqrt{- 1 \times 50}}{5}, \sqrt{- 1} = i = \frac{10 - i \sqrt{25 \times 2}}{5} = \frac{10 - 5 i \sqrt{2}}{5} = 2 - i \sqrt{2}$

أحدد الجزء الحقيقي والجزء التخيلي لكل من الاعداد المركبة التالية ، ثم أمثلها جميعاً في المستوى المركب نفسه .

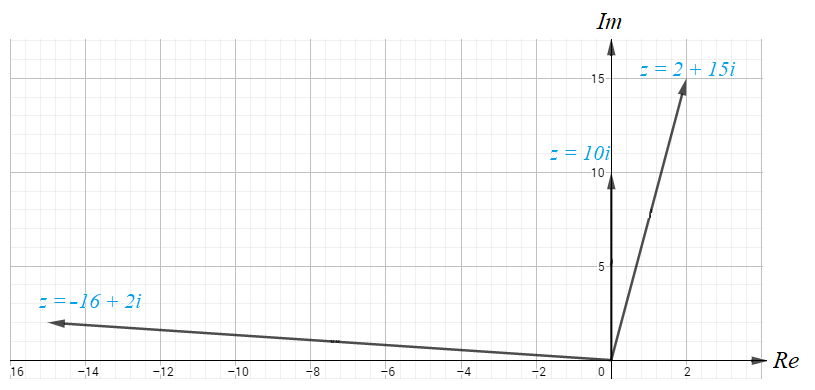
$14) 2 + 15 i S o l u t i o n : R e (z) = 2, I m (z) = 15 15) 10 i S o l u t i o n : R e (z) = 0, I m (z) = 10 16) - 2 - 16 i S o l u t i o n : R e (z) = - 2, I m (z) = - 16$

أمثل العدد المركب ومرافقه بيانياً في المستوى المركب في كل مما يلي :

$17) z = - 15 + 3 i z = - 15 - 3 i$

$18) z = 8 - 7 i z = 8 + 7 i$

$19) z = 12 + 17 i z = 12 - 17 i$

$20) z = - 3 - 25 i z = - 3 + 25 i$

$21) z = 3 i z = - 3 i$

$22) z = 15 z = 15$

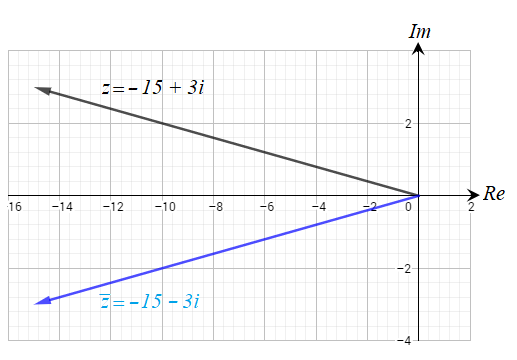
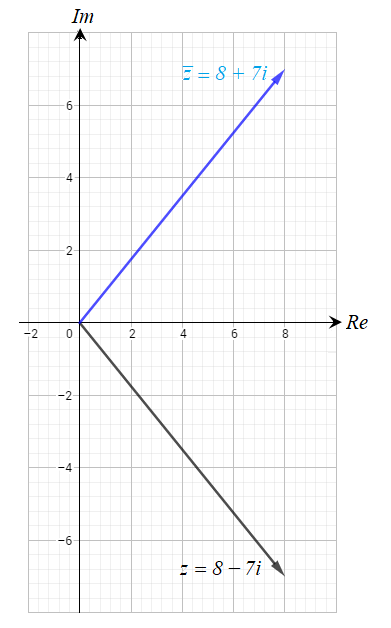
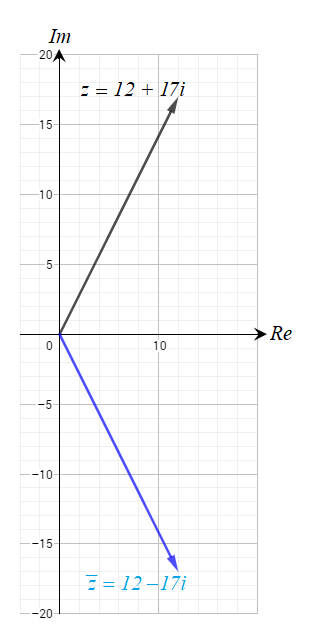
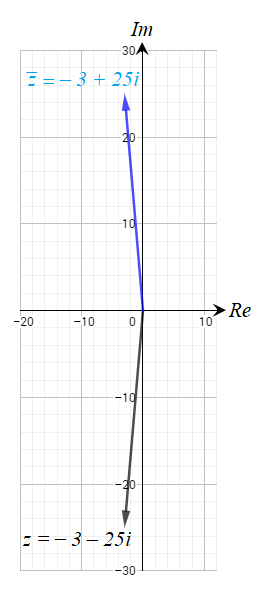
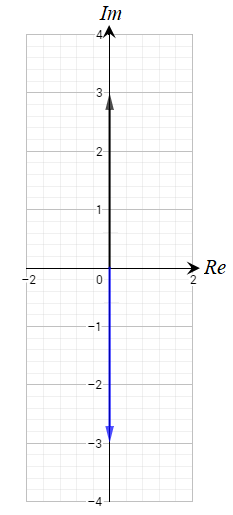
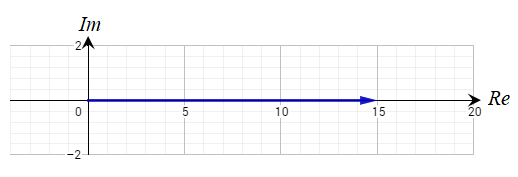
أجد $z, | z |$ ، لكل مما يلي :

$23) z = - 5 + 5 i S o l u t i o n : z = - 5 - 5 i | z | = \sqrt{x^{2} + y^{2}} = \sqrt{{(- 5)}^{2} + {(5)}^{2}} = \sqrt{2 \times 25} = 5 \sqrt{2}$

$24) z = 3 + 3 \sqrt{3} i S o l u t i o n z = 3 - 3 \sqrt{3} i |z| = \sqrt{x^{2} + y^{2}} = \sqrt{{(3)}^{2} + {(3 \sqrt{3})}^{2}} = \sqrt{36} = 6$

$25) z = 6 - 8 i S o l u t i o n : z = 6 + 8 i | z | = \sqrt{x^{2} + y^{2}} = \sqrt{{(6)}^{2} + {(8)}^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10$

أجد قيمة كل من $x, y$ ، الحقيقية التي تجعل كلاً من المعادلات التالية صحيحة :

$26) x^{2} - 1 + i (2 y - 5) = 8 + 9 i S o l u t i o n : R e_{1} = R e_{2} x^{2} - 1 = 8 \Rightarrow x^{2} = 9 \Rightarrow x = \pm 3 I m_{1} = I m_{2} 2 y - 5 = 9 \Rightarrow 2 y = 14 \Rightarrow y = 7$

$27 2 x + 3 y + i (x - 2 y) = 8 - 3 i S o l u t i o n : R e = R e 2 x + 3 y = 8 . . . . . 1 I m = I m x - 2 y = - 3 . . . . . 2 F r o m 1 & 2 2 x + 3 y = 8 - 2 \times (x - 2 y = - 3) - 2 x + 4 y = 6 7 y = 14 \Rightarrow y = 2 x - 2 (2) = - 3 \Rightarrow x = 1$

$28 y - 3 + i (3 x + 2) = 9 + i (y - 4 e) S o l u t i o n : R e = R e y - 3 = 9 \Rightarrow y = 12 I m = I m 3 x + 2 = y - 4 3 x = y - 6 3 x = 12 - 6 \Rightarrow x = 2$

$29 i (2 x - 5 y) + 3 x + 5 y = 7 + 3 i S o l u t i o n : R e = R e 3 x + 5 y = 7 . . . . 1 I m = I m 2 x - 5 y = 3 . . . 2 F r o m 1 & 2 3 x + 5 y = 7 2 x - 5 y = 3 \Rightarrow 5 x = 10 \Rightarrow x = 2 \Rightarrow 3 (2) + 5 y = 7 \Rightarrow y = \frac{1}{5}$

أجد سعة كل من الأعداد المُركَبة الاتية مُقرّبَا إجابتي إلى أقرب منزلتين عشريتين:

$30) 1 S o l u t i o n : z = 1 + 0 i A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{0}{1}) A r g (z) = t a n^{- 1} (0) = 0$

$31) 3 i S o l u t i o n : z = 0 + 3 i A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{3}{0}) A r g (z) = t a n^{- 1} (\infty) = \frac{π}{2}$

$32) - 5 - 5 i S o l u t i o n : z = - 5 - 5 i A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - (π - t a n^{- 1} (\frac{5}{5})) A r g (z) = - (π - t a n^{- 1} (1)) A r g (z) = - (π - \frac{π}{4}) A r g (z) = - \frac{3 π}{4}$

$33) 1 - i \sqrt{3} S o l u t i o n : z = 1 - i \sqrt{3} A r g (z) = - t a n^{- 1} (\frac{b}{a}) A r g (z) = - t a n^{- 1} (\frac{\sqrt{3}}{1}) A r g (z) = - t a n^{- 1} (\sqrt{3}) = - \frac{π}{3}$

$34) 6 \sqrt{3} + 6 i S o l u t i o n : z = 6 \sqrt{3} + 6 i A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{6}{6 \sqrt{3}}) A r g (z) = t a n^{- 1} (\frac{1}{\sqrt{3}}) = \frac{π}{6}$

$35) 3 - 4 i S o l u t i o n : z = 3 - 4 i A r g (z) = - t a n^{- 1} (\frac{b}{a}) A r g (z) = - t a n^{- 1} (\frac{4}{3}) A r g (z) = - t a n^{- 1} (\frac{4}{3}) = - 0.93$

$36) - 12 + 5 i S o l u t i o n : z = - 12 + 5 i A r g (z) = π - t a n^{- 1} (\frac{b}{a}) A r g (z) = π - t a n^{- 1} (\frac{5}{12}) A r g (z) = 3.14 - 0.39 = 2.75$

$37) - 58 - 93 i S o l u t i o n : z = - 53 - 93 i A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - (π - t a n^{- 1} (\frac{93}{58})) A r g (z) = - (π - 1.01) = - 2.13$

$38) - 4 + 2 i S o l u t i o n : z = - 4 + 2 i A r g (z) = π - t a n^{- 1} (\frac{b}{a}) A r g (z) = π - t a n^{- 1} (\frac{2}{4}) A r g (z) = 3.14 - 0.5 = 2.64$

أكتب العدد المُركَّب في كل ممّا يأتي بالصورة المثلثية:

$39) | z | = 2, A r g (z) = \frac{π}{2} S o l u t i o n : z = r (c o s θ + i s i n θ) = 2 (c o s (\frac{π}{2}) + i s i n (\frac{π}{2}))$

$40) | z | = 3, A r g (z) = \frac{π}{3} S o l u t i o n : z = r (c o s θ + i s i n θ) = 3 (c o s (\frac{π}{3}) + i s i n (\frac{π}{3}))$

$41) | z | = 7, A r g (z) = \frac{5 π}{6} S o l u t i o n : z = r (c o s θ + i s i n θ) = 7 (c o s (\frac{5 π}{6}) + i s i n (\frac{5 π}{6}))$

$42) | z | = 1, A r g (z) = \frac{π}{4} S o l u t i o n : z = r (c o s θ + i s i n θ) = (c o s (\frac{π}{4}) + i s i n (\frac{π}{4}))$

$43) z = 6 S o l u t i o n : z = r (c o s θ + i s i n θ) z = 6 + 0 i r = \sqrt{{(6)}^{2} + {(0)}^{2}} = 6 A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{0}{6}) = A r g (z) = t a n^{- 1} (0) = 0 z = r (c o s θ + i s i n θ) = 6 (c o s (0) + i s i n (0))$

$44) z = 1 + i S o l u t i o n : z = r (c o s θ + i s i n θ) z = 1 + i r = \sqrt{{(1)}^{2} + {(1)}^{2}} = \sqrt{2} A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{1}{1}) = A r g (z) = t a n^{- 1} (1) = \frac{π}{4} z = r (c o s θ + i s i n θ) = \sqrt{2} (c o s (\frac{π}{4}) + i s i n (\frac{π}{4}))$

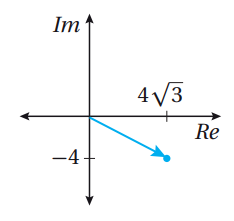
45) يبين الشكل المجاور التمثيل البياني للعدد المركب $z_{1}$ في المستوى المُركَّب ،

أجد العدد المركب $z_{2}$ الذي يحقق : $| z_{2} | = 40, A r g (z_{2}) = A r g (z_{1})$

$S o l u t i o n : z_{1} = 4 \sqrt{3} - 4 i z_{1} = 4 \sqrt{3} + 4 i A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z_{1}) = t a n^{- 1} (\frac{4}{4 \sqrt{3}}) A r g (z_{1}) = t a n^{- 1} (\frac{1}{\sqrt{3}}) = \frac{π}{6} \Rightarrow A r g (z_{2}) = A r g (z_{1}) = \frac{π}{6} z_{2} = r (c o s θ + i s i n θ) z_{2} = 40 (c o s (\frac{π}{6}) + i s i n (\frac{π}{6})) z_{2} = 40 (\frac{\sqrt{3}}{2} + i (\frac{1}{2})) = 20 \sqrt{3} + 20 i$

بفرض أن $z = a + i b$ حيث $| z | = 10 \sqrt{2}$ ، $A r g (z) = \frac{3 π}{4}$ .

46) أكتب العدد المركب z بالصورة القياسية .

$S o l u t i o n : z = r (c o s θ + i s i n θ) z = r (c o s θ + i s i n θ) = 10 \sqrt{2} (c o s (\frac{3 π}{4}) + i s i n (\frac{3 π}{4})) = 10 \sqrt{2} (- \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} i) = 10 \sqrt{2} (\frac{- 1 + i}{\sqrt{2}}) = - 10 + 10 i$

47) أجد قياس الزاوية المحصورة بين $z, z$ .

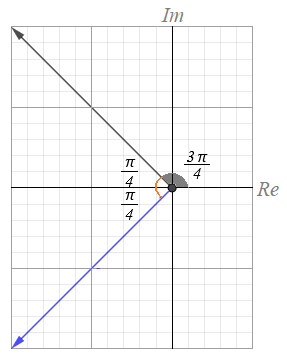
الحل :

الزاوية المحصورة بينهما $2 \times \frac{π}{4} = \frac{π}{2}$

إذا كان $z = - 8 + 8 i$ ، فأجد كلاً مما يأتي :

$48) | z | S o l u t i o n : | z | = \sqrt{x^{2} + y^{2}} | z | = \sqrt{{(- 8)}^{2} + {(8)}^{2}} = \sqrt{2 \times 64} = 8 \sqrt{2}$

$49) A r g (z) S o l u t i o n : z = - 8 + 8 i A r g (z) = π - t a n^{- 1} (\frac{b}{a}) A r g (z) = π - t a n^{- 1} (\frac{8}{8}) A r g (z) = π - t a n^{- 1} (1) A r g (z) = π - \frac{π}{4} = \frac{3 π}{4}$

$50) | z | = | z | S o l u t i o n : 8 \sqrt{2}$

$51) A r g (z) S o l u t i o n : z = - 8 - 8 i A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - (π - t a n^{- 1} (\frac{8}{8})) A r g (z) = - (π - t a n^{- 1} (1)) A r g (z) = - (π - \frac{π}{4}) = - \frac{3 π}{4} O r A r g (z) = - A r g (z)$

تبرير : إذا كان $A r g (5 + 2 i) = α$ ، فأجد سعة كل مما يلي بدلالة $α$ مبرراً اجابتي :

$52) - 5 - 2 i S o l u t i o n : A r g (5 + 2 i) = α α = t a n^{- 1} (\frac{2}{5}) A r g (z) = - (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = - (π - t a n^{- 1} (\frac{2}{5})) = - (π - α) = α - π$

$53) 5 - 2 i S o l u t i o n : A r g (5 + 2 i) = α α = t a n^{- 1} (\frac{2}{5}) A r g (z) = - t a n^{- 1} (\frac{b}{a}) A r g (z) = - α$

$54) - 5 + 2 i S o l u t i o n : A r g (5 + 2 i) = α α = t a n^{- 1} (\frac{2}{5}) A r g (z) = (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = (π - t a n^{- 1} (\frac{2}{5})) = π - α$

$55) 2 + 5 i S o l u t i o n : A r g (5 + 2 i) = α α = t a n^{- 1} (\frac{2}{5}) A r g (z) = t a n^{- 1} (\frac{b}{a}) A r g (z) = t a n^{- 1} (\frac{5}{2}) = \frac{π}{2} - α C o m p l e m e n t t a n^{- 1} (\frac{b}{a}) = \frac{π}{2} - t a n^{- 1} (\frac{a}{b})$

$56) - 2 + 5 i S o l u t i o n : A r g (5 + 2 i) = α α = t a n^{- 1} (\frac{2}{5}) A r g (z) = (π - t a n^{- 1} (\frac{b}{a})) A r g (z) = (π - t a n^{- 1} (\frac{5}{2})) = π - (\frac{π}{2} - α) = \frac{π}{2} + α$

57) تحد: إذا كان $z = 5 + i m$ ، حيث $| z | = 6$ ، و $0 < A r g (z) < \frac{π}{2}$ ، فأجد قيم العدد الحقيقي $m$ .

$S o l u t i o n : z = 5 + i m | z | = \sqrt{x^{2} + y^{2}} 6 = \sqrt{{(5)}^{2} + {(m)}^{2}} 36 = 25 + m^{2} \Rightarrow m^{2} = 11 \Rightarrow m = \pm \sqrt{11} \Rightarrow z = 5 + \sqrt{11} i \Rightarrow A r g (z) = t a n^{- 1} (\frac{\sqrt{11}}{5}) \Rightarrow z = 5 - \sqrt{11} i r e j e c t e d$

58) تبرير: إذا كان $z = 5 + 3 i k$ ، حيث $| z | = 13$ ، فأجد جميع قيم $k$ الحقيقية الممكنة ، مبرراً اجابتي .

$S o l u t i o n : z = 5 + 3 i k | z | = \sqrt{x^{2} + y^{2}} 13 = \sqrt{{(5)}^{2} + {(3 k)}^{2}} 169 = 25 + 9 k^{2} \Rightarrow k^{2} = \frac{144}{9} = 16 \Rightarrow k = \pm 4 \Rightarrow z = 5 + 4 i a n d z = 5 - 4 i$

تحد: بفرض أن $z_{1}$ عدد مركب ، مقياسه $4 \sqrt{5}$ ، وسعته $θ = t a n^{- 1} (2)$ :

59) أكتب $z_{1}$ بالصورة القياسية .

$S o l u t i o n : l e t z = a + b i z = r (c o s θ + i s i n θ) r = \sqrt{a^{2} + b^{2}} 4 \sqrt{5} = \sqrt{a^{2} + b^{2}} \Rightarrow 80 = a^{2} + b^{2} . . . . 1 t a n^{- 1} (\frac{b}{a}) = t a n^{- 1} (2) \Rightarrow \frac{b}{a} = 2 . . . . 2 f r o m 1 & 2 80 = a^{2} + {(2 a)}^{2} 80 = 5 a^{2} \Rightarrow a^{2} = 16 \Rightarrow a = 4 \Rightarrow b = 8 s i n θ = \frac{b}{r} = \frac{8}{4 \sqrt{5}} = \frac{2}{\sqrt{5}} c o s θ = \frac{a}{r} = \frac{4}{4 \sqrt{5}} = \frac{1}{\sqrt{5}} \Rightarrow z = 4 \sqrt{5} (\frac{1}{\sqrt{5}} + i \frac{2}{\sqrt{5}}) \Rightarrow z = 4 + 8 i$

$60$ إذا كان $z_{3} = 7 - 3 i, z_{2} = - 5 + i$ ، فأجد مساحة المثلث الذي رؤوسه $z_{1}, z_{2}, z_{3}$ في المستوى المركب .

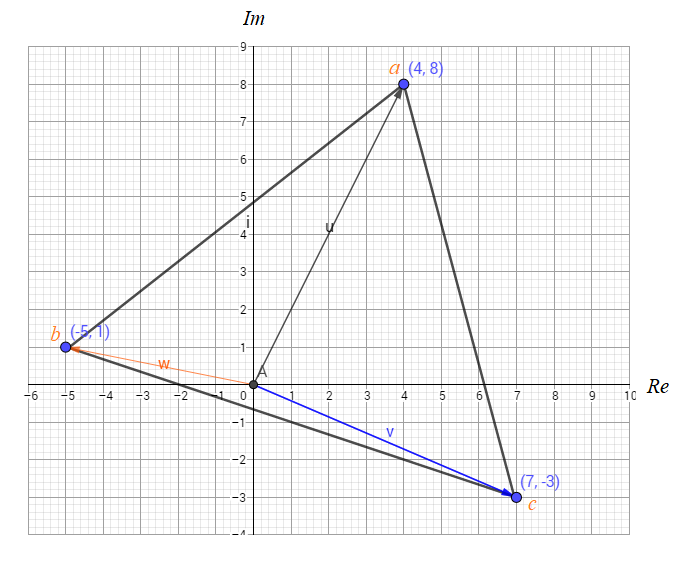
$a b = \sqrt{{(8 - 1)}^{2} + {(4 - - 5)}^{2}} = \sqrt{49 + 81} = \sqrt{130} = 10 \sqrt{13} a c = \sqrt{{(8 - - 3)}^{2} + {(4 - 7)}^{2}} = \sqrt{121 + 9} = \sqrt{130} = 10 \sqrt{13} b c = \sqrt{{(- 3 - 1)}^{2} + {(7 - - 5)}^{2}} = \sqrt{16 + 144} = \sqrt{160} = 4 \sqrt{10}$

فالمثلث $a b c$ متساوي الساقين فيه العامود المقام على القاعدة ينصفها ،

إحداثيات منتصف القاعدة $(\frac{- 5 + 7}{2}, \frac{1 + - 3}{2}) = (1, - 1)$

فالارتفاع $\sqrt{{(8 - - 1)}^{2} + {(4 - 1)}^{2}} = \sqrt{81 + 9} = \sqrt{90} = 3 \sqrt{10}$

مساحة المثلث $A = \frac{1}{2} (4 \sqrt{10}) (3 \sqrt{10}) = 60$

رياضيات فصل أول

التوجيهي علمي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS