أتحقق من فهمي
ص: 61
إذا كان ، فأجيب عما يأتي:
a) أمثل الاقتران بيانيا، ثم أجد مجاله ومداه وخطوط التقارب.
مجال الاقتران هو الأعداد الحقيقية ومداه الفترة وله خط تقارب أفقي هو المحور x.
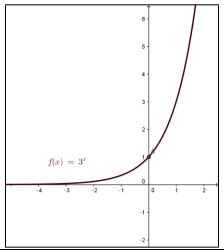
b) أجد المقطع x والمقطع y.
ليس للإقتران مقطع x وله مقطع y هو 1 عند x=0
c) هل f(x) متزايد أم متناقص؟
الاقتران متزايد
d) هل f(x) هو اقتران واحد لواحد؟
الاقتران واحد لواحد
أتحقق من فهمي
ص: 63
إذا كان ، فأجيب عما يأتي:
a) أمثل الاقتران بيانيا، ثم أجد مجاله ومداه وخطوط التقارب.
مجال الاقتران هو الأعداد الحقيقية ومداه الفترة وله خط تقارب أفقي هو المحور x
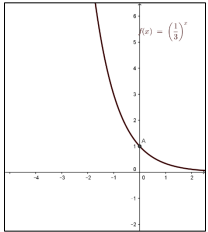
b) أجد المقطع x والمقطع y.
ليس للإقتران مقطع x وله مقطع y هو 1 عند x=0
c) هل f(x) متزايد أم متناقص؟
الاقتران متناقص
d) هل f(x) هو اقتران واحد لواحد؟
الاقتران واحد لواحد
أتحقق من فهمي
ص: 65
أجد خط التقارب الأفقي لكل مما يأتي، وأمثله بيانيا وأجد مجاله ومداه:
خط التقارب الأفقي y=12 مجال الإقتران الأعداد الحقيقية R المدى في الفترة .
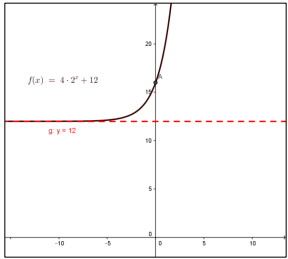
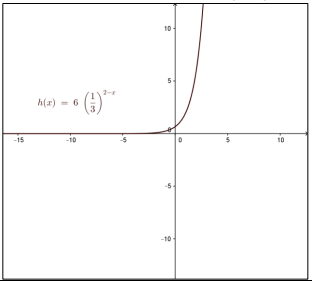
خط التقارب الأفقي هو محور x
مجال الإقتران الأعداد الحقيقية R المدى في الفترة .
أتحقق من فهمي
ص: 66
تمثل المعادلة الكمية المتبقية N بالغرامات من عينة كتلتها 1g من السيزيوم 137 حيث t الزمن بالسنوات.
a) أجد كمية السيزيوم 137 المتبقية بعد 30 سنة.
كمية السيزيوم 137 المتبقية بعد 30 سنة هي
b) بعد كم سنة يبقى من كمية السيزيوم 0.25g.
إذن بعد 60 سنة يبقى من (السيزيوم 137) 0.25g.
أتحقق من فهمي
ص: 67
بلغ عدد سكان لواء الموقر في عام 2015 تقريبا 84370 نسمة، فإذا كانت نسبة النمو السكاني فيه %2.4 سنويا، فأجيب عما يأتي:
a) أكتب اقتران النمو الأسي الذي يمثل عدد سكان لواء الموقر بعد t سنة منذ العام 2015.
b) أجد عدد سكان اللواء التقريبي في عام 2050.
عام 2015 هو القيمة الابتدائية أي عند t=0 فعند عام 2050 تكون قيمة t=35
فيكون عدد السكان عام 2050 تقريبا 193502 نسمة.
c) أمثل اقتران النمو الأسي بيانيا.
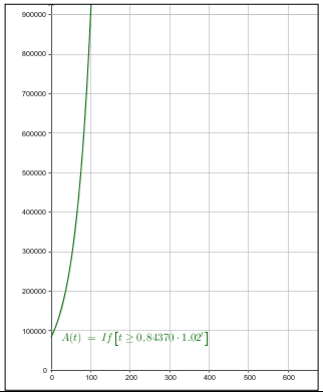
أتحقق من فهمي
ص: 69
سيارة: اشترى أحمد سيارة تعمل على الشحن الكهربائي بمبلغ 25000 JD. إذا كان ثمن السيارة يقل بنسبة %10 سنويا؛ فأجيب عما يأتي:
a) أكتب اقتران الاضمحلال الأسي لثمن السيارة بعد (t) سنة.
b) أجد ثمن السيارة بعد 5 سنوات.
c) أمثل اقتران الاضمحلال بيانيا.
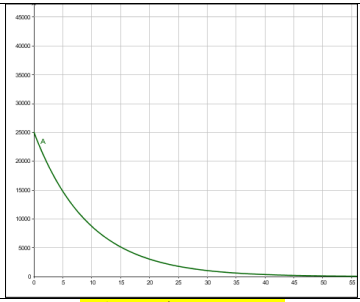
أتحقق من فهمي
ص: 70
يمثل الاقتران عدد سكان مدينة بالمليون نسمة، بعد t سنة منذ المسح الإحصائي للمدينة في عام 2015.
a) أجد عدد سكان المدينة في عام 2015.
عام 2015 تكون t=0
b) أجد عدد سكان المدينة في عام 2030؛ مقربا إجابتي إلى أقرب مليون
عام 2030 تكون t=15
أتدرب وأحل المسائل
أمثل كل من الاقترانات الآتية بيانيا وأجد مجاله ومداه:
مجال الاقتران الأعداد الحقيقية R المدى الفترة .
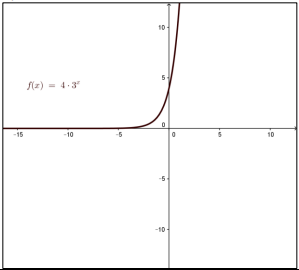
مجال الاقتران الأعداد الحقيقية R المدى الفترة
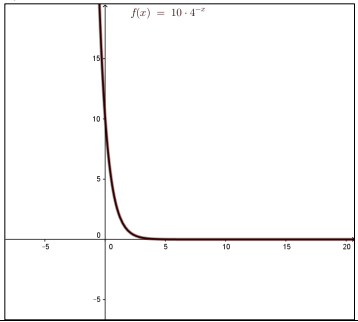
مجال الاقتران الأعداد الحقيقية R المدى الفترة
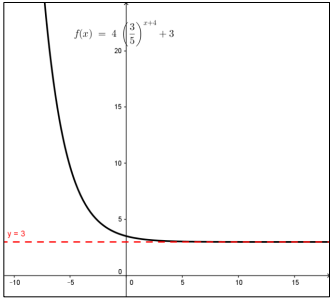
مجال الاقتران الأعداد الحقيقية R المدى الفترة
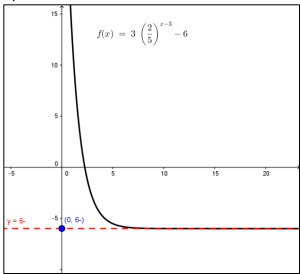
مجال الاقتران الأعداد الحقيقية R المدى الفترة
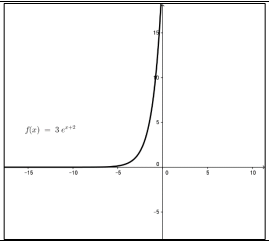
مجال الاقتران الأعداد الحقيقية R المدى الفترة
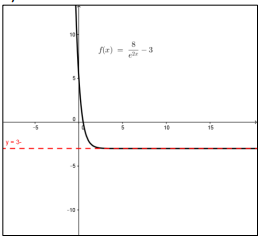
أشجار: يمثل الاقتران طول شجرة من التين الخانق f(x) بالأقدام بعد x سنة.
7) أجد خط التقارب الأفقي للاقتران f(x)، ثم أمثله بيانيا، علما بأن x=0 تمثل الوقت الحاضر.
خط التقارب الأفقي هو محور x.
8) أجد المقطع y للاقتران f(x) وأصف مدلوله.
أجد المقطع y
وهذا يعني طول الشجرة الحالي هو 12 قدم لأن x=0 تمثل الوقت الحاضر
يبين التمثيل البياني المجاور العلاقة بين عدد الخلايا البكترية في عينة مخبرية والزمن بالساعات.
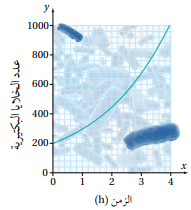
9) أجد عدد الخلايا البكتيرية في البداية.
من الرسم البياني يتضح أن عدد الخلايا في البداية (عند h=0) هو a=200 خلية
10) أجد النسبة المئوية للنمو في كل ساعة.
من الرسم البياني أجد أن قيمة عدد خلايا البكتيريا A عند h=2 هو 440 خلية وهو إقتران نمو أسي إذن:
11) أكتب اقتران النمو الأسي الذي يمثل عدد الخلايا البكتيرية بعد h ساعة.
12) بعد كم ساعة يصبح عدد الخلايا البكترية 3 أضعاف عددها الأصلي.
من الرسم نجد قيمة h عند A=600 فيكون تقريبا 2.8 ساعة.
يمر منحنى الاقتران بالنقطتين .
13) أجد قيمة كل من الثابتين k و c.
14) أجد قيمة y عندما x=3
يظهر التمثيل البياني المجاور العلاقة بين ثمن دراجة نارية بالدينار والزمن بالسنوات.
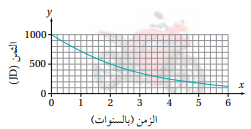
15) أجد ثمن الدراجة بالدينار عند شرائها.
ثمن الدراجة عند شرائها أي عند t=0 وهو 1000JD
16) أجد النسبة المئوية للاضمحلال في ثمن الدراجة.
من الرسم أجد أن ثمن الدراجة عند t=2 وهو P(2)=500
وبما أن الثمن عند t=0 هو a=1000 إذن:
17) أكتب اقتران الاضمحلال الأسي الذي يمثل ثمن الدراجة بعد مرور (t) سنة.
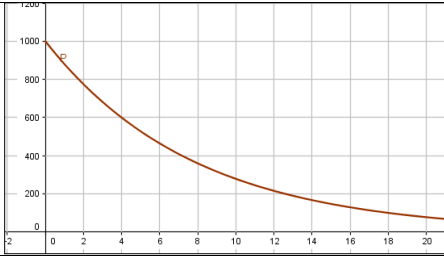
يقاس الضغط الجوي بوحدة تسمى الهيكتوباسكال (hPa)، ويكون الضغط الجوي عند سطح البحر 1000hPa، ويتناقص بنسبة %12 لكل كيلومتر ارتفاعا عن سطح البحر.
18) أكتب الاقتران الاضمحلال الأسي للضغط الجوي عند ارتفاع (h) كيلومتر.
عند سطح البحر تكون h=0 أي أن الضغط عند البداية يكون 1000
19) أمثل اقتران الاضمحلال بيانيا.
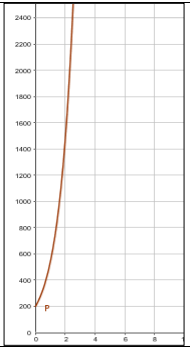
يمثل الاقتران عدد أسماك السلمون P في نهر بعد t سنة.
20) أجد عدد أسماك السلمون في النهر بعد 3 سنوات.
21) أمثل الاقتران P(t) بيانيا باستعمال برمجية جيوجيبرا.
22) طب: حقن الطبيب مريضا بمادة علاجية، فإذا كان تركيز هذه المادة في جسم المريض يقل بنسبة %40 يوميا؛ فأكتب اقتران الاضمحلال الذي يمثل تناقص تركيزه المادة العلاجية M بعد t يوم.
مهارات التفكير العليا
23) أكتشف الخطأ: تقول سميرة إن العلاقة بين ثمن عقار والزمن بالسنوات الممثلة في الشكل المجاور، تمثل اقتران نمو أسي لأن ثمن العقار يزداد مع الزمن: هل هي على صواب؟ أبرر إجابتي.
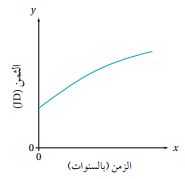
خطأ، لأن الرسم البياني على الشكل الإقتران الأسي حيث أن الإقتران الأسي المتزايد يكون مقعرا للأعلى وليس للأسفل
24) تحد: إذا كانت ؛ فأكتب كلا من المقادير الآتية بدلالة P:
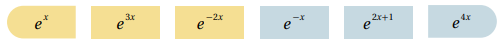
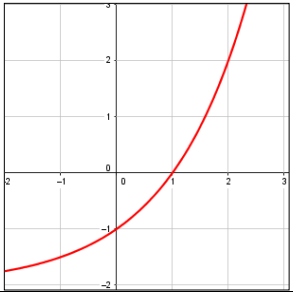
25) تبرير: متى يقطع الاقتران الأسي محور x ؟ أبرر إجابتي بتقديم مثال داعم.
الأقتران الأسي يقطع محور x إذا كان على صورة حيث c<0 مثل حيث يكون تمثيله البياني كما في الشكل المجاور:
26) تحد: أحدد العلاقة بين الاقترانين . أبرر إجابتي.