رياضيات أدبي فصل ثاني

حلول أسئلة كتاب الطالب وكتاب التمارين

حلول أسئلة أتحقق من فهمي

اتحقق من فهمي صفحة 10

إذا كان:  $\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}\mathrm{x} + 1 , \mathrm{x} < 1\\ 3 - \mathrm{x} , \mathrm{x} > 1\end{array}$ ، فأجيب عن الأسئلة الآتية:

 

a) أُحدد مجال f(x).

المجال هو: $(-\infty , \infty ) - \left\{1\right\}$

 

b) أجد قيمة كل من : f(-1)،  وf(1)،  وf(3).

f(-1) = x + 1

         =  -1 + 1 = 0

f(1)    ==>    غير معرف لأنّ العدد (1) لا ينتمي لمجال الاقتران

f(3) = 3 - x

        = 3 - 3 = 0

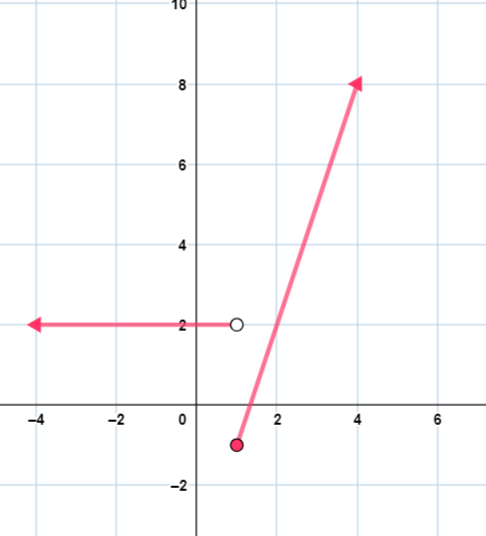
c) أمثل الاقترانf(x)  بيانيا، ثم أحدّد مداه.

 تمثيل القاعدة x + 1   ، عند 1  > x    ، وضعْ دائرة مُفرغة عند (1 , 2)

-1	1	x
0	2	Y = x + 1
(-1 , 0)	( 1 , 2)	(x , y)

 

 

 

 

 

 

تمثيل القاعدة 3 - x   ، عند 1 <  x  ، وضعْ دائرة مُفرغة عند (1 , 2)

2	1	x
1	2	Y = 3 - x
(2 , 1)	(1 , 2)	(x , y)

 

 

 

 

 

 

المدى$(-\infty , 2)$

 

---

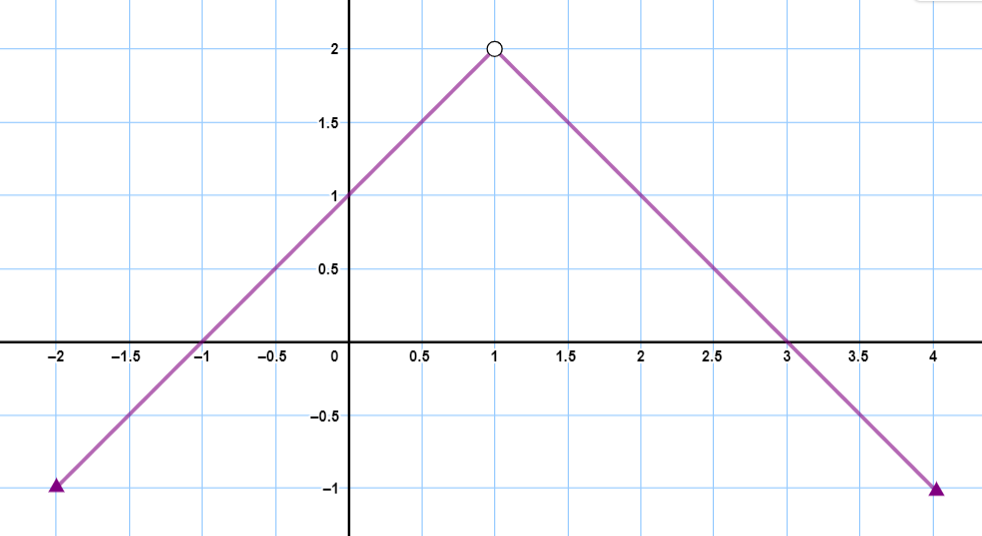
اتحقق من فهمي صفحة 11 أكتب قاعدة الاقتران المتشعب الممثل بيانيًا في الشكل المجاور.
الحل:
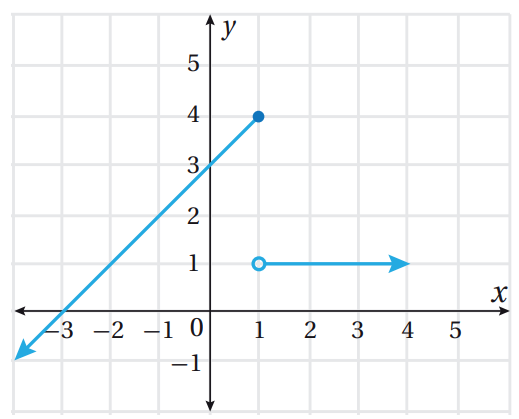
أكتب الاقتران الذي يُمثل كل جزء في التمثيل البياني :

الخطوة 1: أكتب قاعدة الاقتران الذي يُمثل الجزء الأيسر من التمثيل البياني، وهو شعاع يمر بالنقطتين  -3 , 0))، (4 , 1).

وميله:    $m = \frac{y_2 - y_1}{x_2 - x_1}= \frac{0 - 4}{-3 -1}= \frac{-4}{-4}=1$   

ثم، نكتب معادلة الخط المستقيم بصيغة الميل والمقطع، وهي: y = m x + b   

إذن؛    y  =  x + 3    (بتعويض الميل m = 1 ، والمقطع b = 3 في المعادلة)

ويُمكن كتابتها في صورة: f(x) = x + 3  

 

أما وجود دائرة  مظللة عند النقطة (4 , 1) فيعني أن هذه القاعدة تُقابل الفترة ]1  , ¥-) من مجال الاقترانf(x)  ، أي:  1 ≥ x  

 

الخطوة 2: أكتب قاعدة الاقتران الذي يُمثل الجزء الأيمن من التمثيل البياني، وهو خط مستقيم يوازي محور x   ، (اقتران ثابت)، قاعدته:  y = 1  ، ووجود دائرة مُفرغة عند النقطة (1 ,  1)  

فهذا يدل على أن هذه القاعدة تقابل الفترة $(1 , \infty )$ من مجال الاقتران f(x)  ، أي :  1  < x       

 

إذن ، قاعدة هذا الاقتران هي:   $\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}\mathrm{x} + 3 , \mathrm{x} \le 1\\ 1 , x>1\end{array}$

---

اتحقق من فهمي صفحة 12

قررت إدارة أحد المستشفيات الخاصة زيادة الرواتب الشهرية للأطباء والطبيبات وفق الأسس الآتية:

• زيادة الرواتب التي تقل عن 700 JD بنسبة 15%.

• زيادة الرواتب التي تتراوح بين 700  JDوأقل من 1000 JD بنسبة 10%.

• زيادة الرواتب التي تبلغ 1000 JD فأكثر مبلغ 50 JD.

أكتب اقترانا متشعبا يُمكن استعماله لإيجاد الراتب الجديد لأي طبيب أو طبيبة في هذا المستشفى.

الحل:

افرض قيمة الراتب = x   

• زيادة الرواتب التي تقل عن 700 JD بنسبة 15%   

←  الزيادة  =  0.15 x  ، للرواتب في الفترة :  700  >  x     

 

• زيادة الرواتب التي تتراوح بين 700  JD وأقل من 1000  JD  بنسبة 10%

← الزيادة  = 0.1 x  ، للرواتب في الفترة 1000 >  x  ≥  700        

 

• زيادة الرواتب التي تبلغ 1000 JD فأكثر ، مبلغ 50 JD

← الزيادة  =   50  ، للرواتب في الفترة x  ≥ 1000

الراتب الجديد = الراتب الأصلي  + الزيادة

إذن الاقتران المتشعب الذي يمثل الرواتب بعد الزيادة هو :                       

$\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}1.15 x , \mathrm{x} < 700\\ 1.1 x , 700 \le \mathrm{x} <10000\\ x + 50 , \mathrm{x} \ge 10000\end{array}$     $\stackrel{\mathrm{ومنه}}{\to }$     $\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}\mathrm{x} + 0.15 x , \mathrm{x} < 700\\ \mathrm{x} + 0.1 x , 700 \le \mathrm{x} <10000\\ x + 50 , \mathrm{x} \ge 10000\end{array}$

---

حلول أسئلة أتدرّب وأحُلُّ المسائل

إذا كان: $f\left(x\right) = \{\begin{array}{l}3\mathrm{x} - 4 , \mathrm{x} \ge 1\\ 2 , \mathrm{x} < 1\end{array}$ ، وكان: $g\left(x\right) = \{\begin{array}{l}2\mathrm{x} + 1 , -3 \le \mathrm{x} < 0\\ 2\mathrm{x} - 1 , \mathrm{x} > 0\end{array}$ ، فأجيب عن الأسئلة الآتية:

1) أُحدّد مجال كلّ من:f(x) ، وg(x)

مجال f(x) هو: $(-\infty , \infty )$      ،     مجال g(x) هو: $[-3 , \infty ) - \left\{0\right\}$

 

2) أجد قيمة كلّ من: f(-1)، وf(2)، وg(0)، g(-2).

f(-1) = 2    

f(2) = 3x - 4

       = 3(2) - 4 = 2   

g(0)    ==>    g(x) غير معرف لأنّ العدد (0) لا ينتمي لمجال الاقتران

g(-2) = 2x + 1

          = 2(-2) + 1 = -3 

3) امثل الاقتران f(x) بيانيًا، ثم أحدّد مداه.

الحل:

تمثيل القاعدة الأولى ، ووضع حلقة مُظللة عند (1- , 1)

2	1	x
2	-1	Y = 3x - 4
( 2 , 2)	( 1 , -1)	(x , y)

 

 

 

 

 

 

تمثيل القاعدة الثانية  y = 2 ، وهو خط مستقيم يوازي محور x  ،    ووضع حلقة مُفرغة عند النقطة   (1 , 2)؛ لعدم وجود مساواة في الفترة. المدى: $\mathbf{[}\mathbf{-}\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{\infty }\mathbf{)}$

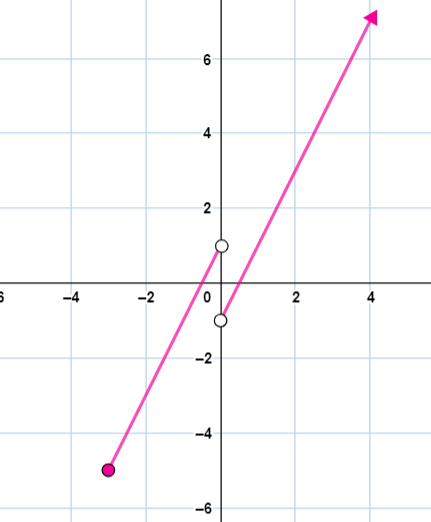
4) امثل الاقتران g(x) بيانيًا، ثم أحدّد مداه.   

الحل:

تمثيل القاعدة الأولى ، ووضع حلقة مُظللة عند (-3 , - 5) ، وحلقة مُفرغة عند (0 , 1)
0	-3	x
1	-5	Y = 2x + 1
( 0 , 1 )	( -3 , -5)	(x , y)
تمثيل القاعدة الثانية ، ووضع حلقة مفرغة عند           (0 , - 1).

1	0	x
1	-1	Y = 2x -1
(1 , 1)	(0 , -1)	(x , y)

---

 

 

 

 

 

المدى  $[-5 , \infty )$

---

اكتب قاعدة الاقتران المتشعب المُمثل بيانيًا في كل مما يأتي:  

$f\left(x\right) = \{\begin{array}{l}4 , \mathrm{x} \ge 2\\ -4 , \mathrm{x} < 2\end{array}$

 

 

 

 

 

 

 

 

 

 

$f\left(x\right) = \{\begin{array}{l}-\frac{5}{3}x - \frac{8}{3} , \mathrm{x} \le -1\\ \frac{4}{3}x - \frac{2}{3} , -1< \mathrm{x} \le 2\\ -3 , x > 2\end{array}$

 

 

 

 

 

 

 

 

 

 

$f\left(x\right) = \{\begin{array}{l}2 , \mathrm{x} <-4\\ -x - 2 , -4< \mathrm{x} < 2\\ x - 6 , x > 2\end{array}$

 

 

 

 

 

 

 

 

 

 

$f\left(x\right) = \{\begin{array}{l}-4 , \mathrm{x} \le -2\\ x - 2 , -2< \mathrm{x} \le 2\\ -1.75x + 3.5 , x > 2\end{array}$

 

 

 

 

 

 

 

 

 

 

 

---

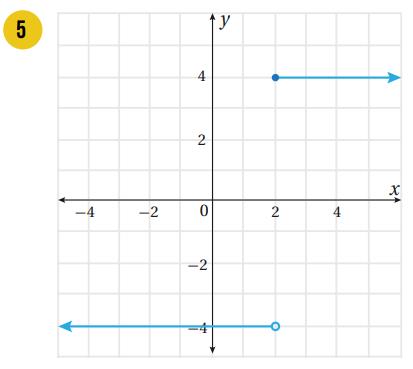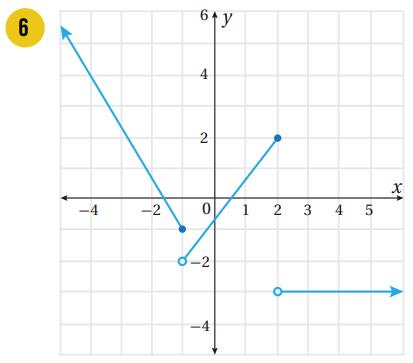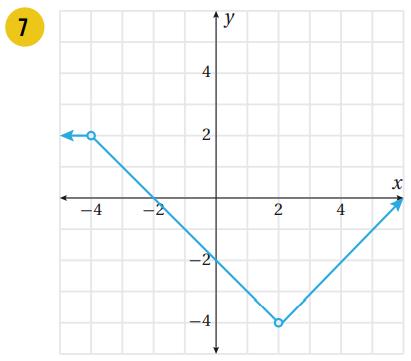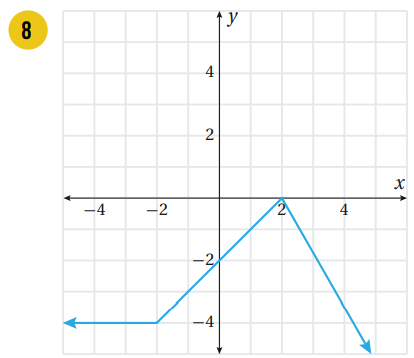9) توفير : أراد الوالد أن يحفز ابنته سعاد على توفير جزء من مصروفها اليومي ، فقرر منحها مبلغا يساوي ما ستوفره نهاية كل شهر ن في حال لم يتجاوز مبلغ التوفير 5 JD . أما إذا زاد على ذلك ، فإنه سيمنحها 10JD . اكتب اقترانا متشعبا يُمكن استعماله لتمثيل هذا الموقف.

الحل:

افرض المبلغ الذي ستوفره سعاد = x

إذن سيمنح الوالد x   دينار(نفس مبلغ التوفير) في حال كان مبلغ التوفير أقل من 5 ، وسيمنح 10 دنانير إذا كان مبلغ التوفير أكبر من 5

وبهذا يصبح مع سعاد  2x  ، إذا كان   ≤  5  x  ،    و   x + 10   ،   إذا كان  5  x  >  

إذن الاقتران الذي يمثل الموقف هو:  $f\left(x\right) = \{\begin{array}{l}2x ,0\le \mathrm{x} \le 5\\ x+10 , \mathrm{x} > 5\end{array}$

---

10) أعمال : يعمل مندوب مبيعات لدى شركة لقاء راتب شهري مقداره 500JD ، وعمولة شهرية نسبتها 1% عن أول 2000 JD  لثمن مبيعاته. وفي حال زادت المبيعات الشهرية على 2000 JD ، فإنه يستحق عمولة نسبتها 1.5% عن المبلغ الذي يزيد على 2000 JD . اكتب اقترانا متشعبا يمكن استعماله لحساب الدخل الشهري لمندوب المبيعات.

الحل :

افرض ثمن مبيعات المندوب = x ، إذن؛

سيتقاضى المندوب  500 + 0.01x  عندما  x ≤ 2000  

وسيتقاضى 20 JD نسبته عن أول 2000 دينار    +   0.015 (x – 2000) نسبته عن المبيعات التي تزيد عن 2000  + 500   (الراتب) ، عندما 2000   <  x

إذن الاقتران الذي يمثل الموقف هو: $f\left(x\right) = \{\begin{array}{l}500 + 0.1x , \mathrm{x} \le 2000\\ 490 + 0.015x , \mathrm{x} > 2000\end{array}$

---

11) أحل المسالة الواردة في بند مسألة اليوم

مسألة اليوم: اتفقت مريم مع إحدى دور النشر على بيع كتاب لها لقاء حصولها على ما نسبته 10% من قيمة مبيعات أول 10000 نسخة من الكتاب ، و 15% من قيمة أي مبيعات إضافية . إذا كان ثمن الكتاب الواحد 7 JD ، فما المبلغ الذي ستأخذه  مريم بعد بيع 12000

الحل :

ثمن الكتاب الواحد = JD 7   ←  ثمن 10000 كتاب = 70000 JD

إذن تأخذ مريم 70000 ×  0.1 =  7000 JD  عن أول 10000 كتاب.

لكن مريم باعت 12000 كتاب ، ثمن 2000 كتاب  = 2000 × 7 = 14000 JD

إذن ستأخذ مريم عن 2000 كتاب 0.15 × 1400 = 2100 JD

مجموع ما ستأخذه مريم = 7000 + 2100 = 9100 JD

 

ويُمكن كتابة اقتران متشعب يُمثل هذا الموقف :

افرض عدد الكتب   = x   ← الثمن  = 7x

$\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}0.7x , \mathrm{x} \le 10000\\ 1.05x - 3500 , x > 10000\end{array}$       $\stackrel{\mathrm{وبالتبسيط}}{\to }$     $\mathrm{f}\left(\mathrm{x}\right) = \{\begin{array}{l}0.1 \left(7x\right) , \mathrm{x} \le 10000\\ 7000 + 0.15 \left(7\right) (x - 10000) , x > 10000\end{array}$

           

---

حلول أسئلة مهارات التفكير العُليا

12) تبرير : ادعت سارة أنه يُمكنها تمثيل الاقتران المتشعب $f\left(x\right) = \{\begin{array}{l}\mathrm{x} + 4 , \mathrm{x} < -2\\ -2\mathrm{x} - 2 , \mathrm{x} \ge -2\end{array}$   بسهولة، وذلك بتمثيل كل من قاعدتيه بيانيًا، وافتراض أنّ مجال كل منهما على حدة هو مجموعة الأعداد الحقيقية كلها، ثم محو  أجزاء المنحنى التي تقع خارج المجال المُحدد في الاقتران المتشعب كما في الشكل الآتي. هل ادّعاء سارة صحيح؟ أُبرر إجابتي.

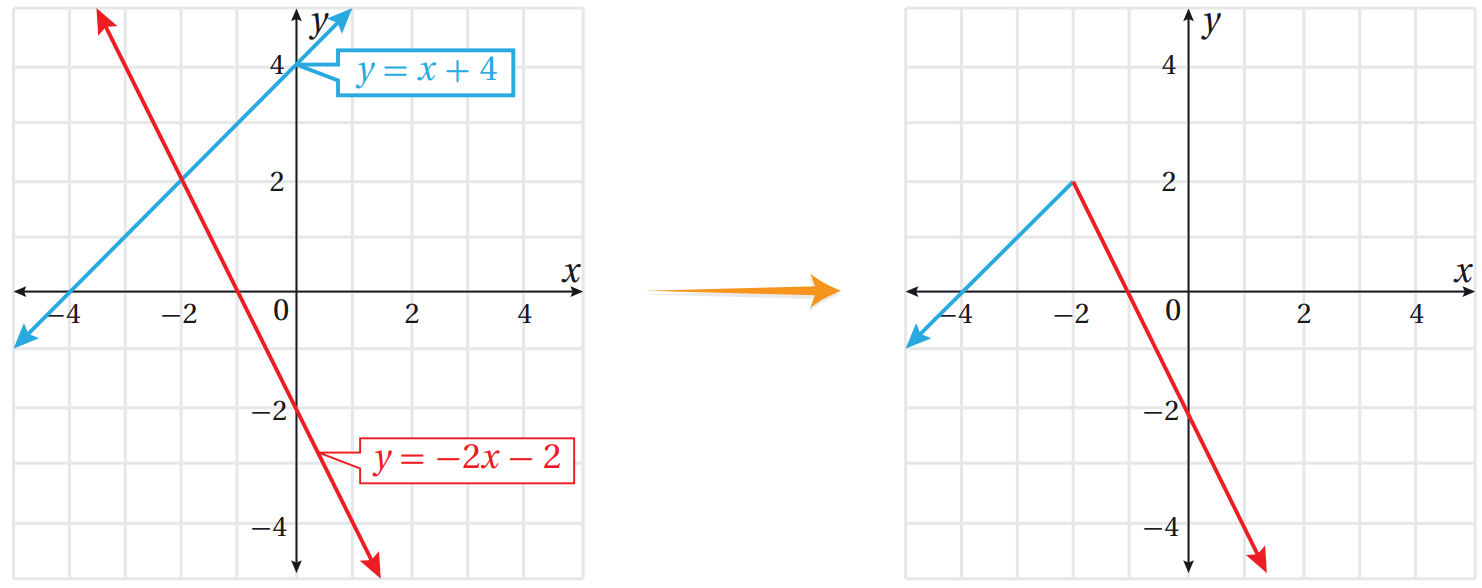
الحل:

نعم ، ادّعاء سارة صحيح ؛ لأن الاقتران المتشعب مُعرف بقواعد مختلفة لأجزاء من مجاله ، وحيث قامت سارة بمحو الأجزاء التي تقع خارج المجال المُحدد لكل قاعدة في الاقتران ، فالتمثيل صحيح.   

---

13) مسألة مفتوحة : أكتب اقترانًا متشعبًا f(x)، بحيث  f(-2) = f(-1) = 3  ،  و  f(2) = f(3) = 5.

الحل:

$f\left(x\right) = \{\begin{array}{l}3 , \mathrm{x} < 2\\ 5 , \mathrm{x} \ge 2\end{array}$

---

14) تحدِّ : أُمثّل الاقتران المتشعب$h\left(x\right) = \{\begin{array}{l}3 , \mathrm{x} = 1\\ 2 - \mathrm{x} , \mathrm{x} \ne 1\end{array}$ بيانيًا، ثمّ أحدّد مجاله ومداه.  

الحل:

المجال:(- ∞ , ∞)     المدى: (- ∞ , ∞)

---

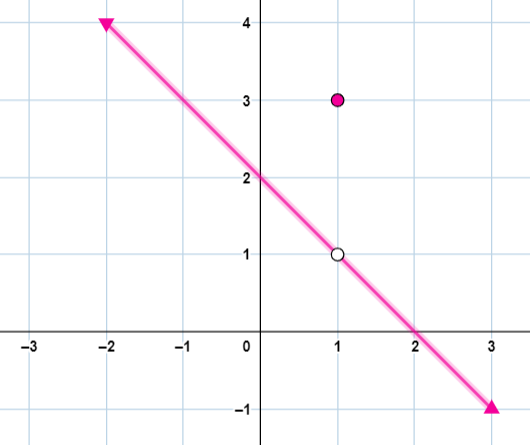حلول أسئلة كتاب التمارين  

إذا كان: $f\left(x\right) = \{\begin{array}{l}2x + 1 , \mathrm{x} < 0\\ 1 - x , \mathrm{x} \ge 0\end{array}$ ، فأجيب عن الأسئلة الآتية:

1) أحدد مجال الاقترانf(x) .

المجال: (- ∞ , ∞)

---

2) أجد قيمة كل من: f(-2) ، f(0) ، f(1)

f(1) = 1 - x 

       = 1 - 1 = 0    

f(0) = 1 - x

       = 1 - 0 = 1  

f(-2)  = 2x + 1

          = 2(-2) + 1 = -3

3) أمثل الاقترانf(x)  بيانيًا، ثم أحدد مجاله ومداه.  

---

أكتب قاعدة الاقتران المتشعب الممثل بيانًا في كل مما يأتي :

$f\left(x\right) = \left\{\begin{array}{l}-2x -1 , x \le 2 \\ 4 - x , x > 2\end{array}\right.$

 

 

 

 

 

 

 

 

 

 

$f\left(x\right) = \{\begin{array}{l}-4 , x \le -2 \\ x - 2 , -2< x \le 2\\ 4 - 2x , x > 2\end{array}$

 

 

 

 

 

 

 

 

 

 

---

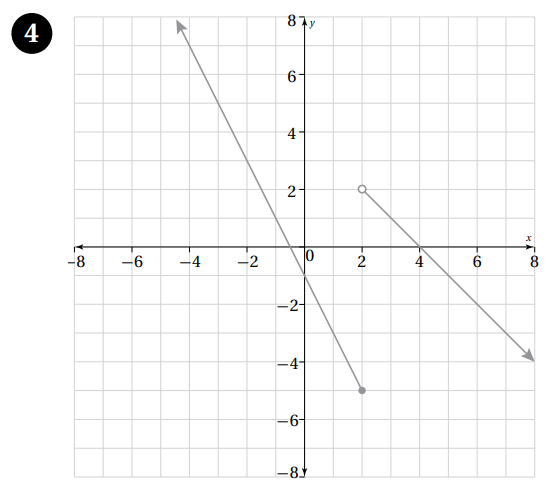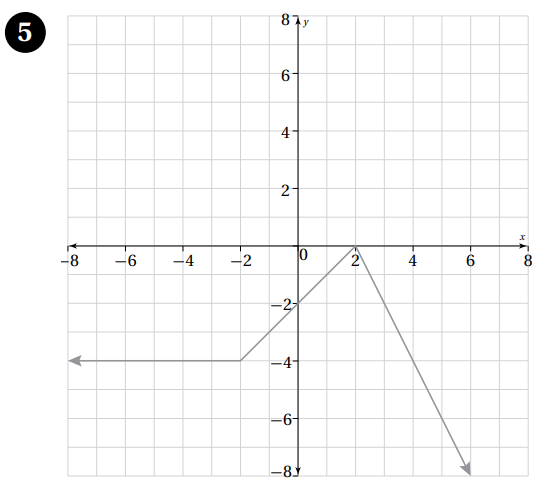6) تأجير سيارات: قدمت شركة لتأجير السيارات عرضًا يتضمن تأجير أي من سياراتها بمبلغ 15 دينار يوميًا ؛ بشرط قيادة السيارة المستأجرة مسافة لا تزيد عن 300Km في اليوم الواحد . وفي حال تجاوز هذه المسافة في اليوم الواحد يتعين على المُستأجر دفع مبلغ 20 دينار . أكتب اقترانا متشعبا يُمثل قيمة استئجار سيارة من هذه الشركة وقيادتها مسافة x  كيلو مترًا مدة يوما واحد.

الحل :

افرض المسافة التي يقطعها المُستأجر = x  

إذن يدفع المُستأجر 15 دينار في اليوم عندما  300 x ≤  

ويدفع المُستأجر  20 دينار في اليوم  عندما  x > 300

الاقتران المُتشعب الذي يمثل الموقف لمدة يوم واحد هو:  $f\left(x\right) = \{\begin{array}{l}15 , x \le 300 \\ 20 , x > 300\end{array}$

---

7) خدمات شحن: تأخذ شركة للشحن مبلغ 12 دينارًا لقاء شحن كل طرد كتلته 5Kg ، أو أقل ، ومبلغ 14 دينارًا عند شحن طرد  كتلته أكثر من 5Kg ، اكتب اقترانا متشعبًا يُمثل قيمة شحن طرد تتراوح كتلته بين 0Kg و 8Kg.

الحل :

افرض كتلة الطرد x

تأخذ الشركة مبلغ 12 دينار   ، عندما    x ≤ 5

وتأخذ الشركة مبلغ 14 دينار ، عندما   x >  5

المطلوب كتابة اقتران متشعب يُمثل قيمة شحن طرد تتراوح كتلته بين 0Kg و 8Kg .

$f\left(x\right) = \{\begin{array}{l}12 , 0 < x \le 5 \\ 14 , 5 < x \le 8\end{array}$