الاقترانات المثلثية
تعرفنا سابقاً على الاقترانات المثلثية وهي عبارة عن قاعدة معطاة باستعمال النسب المثلثية وعددها ست اقترانات مرتبطة بست نسب مثلثية تحددها.
|
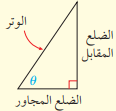
إذا مثلث قياس زاوية حادة في مثلث قائم الزاوية، فإن الاقترانات المثلثية الستة تعرف بدلالة الوتر، والضلع المقابل، والضلع المجاور كما يأتي:
|
ملاحظة:
قاطع التمام هو مقلوب نسب الجيب
القاطع هو مقلوب جيب التمام
ظل التمام هو مقلوب الظل
لذلك يطلق على اقترانات قاطع التمام والقاطع وظل التمام اسم اقترانات المقلوب
مثال:
أجد قيم الاقترانات المثلثية الستة للزاوية في المثلث المجاور
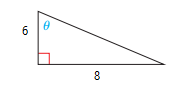
1) نجد طول الوتر باستعمال نظرية فيثاغورس
ق
لاحظ ان الطول لا يمكن ان يكون سالب
2) أجد الاقترانات المثلثية للزاوية .
sin ==
cos ==
tan ==
csc ==
sec ==
cot ==
إيجاد قيم الاقترانات المثلثية باستعمال نقطة معلومة
|
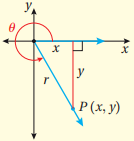
إذا كانت زاوية مرسومة في الوضع القياسي، والنقطة p (x, y) تقع على ضلع الانتهاء للزاوية ، r يمثل البعد بين النقطة P ونقطة الأصل، حيث: , ، فان الاقترانات المثلثية للزاوية تعرف كما يأتي:
|
مثال:
إذا وقعت النقطة (4-, 2) على ضلع انتهاء الزاوية المرسومة في الوضع القياسي فإن قيم الاقترانات المثلثية الستة للزاوية هي:
sin =
cos =
tan =
csc =
sec =
cot =
إيجاد قيم الاقترانات المثلثية للزاويا الربعية:
الزاوية الربعية هي الزاوية في الوضع القياسي التي ينطبق ضلع انتهائها على أحد المحوريين الإحداثيين
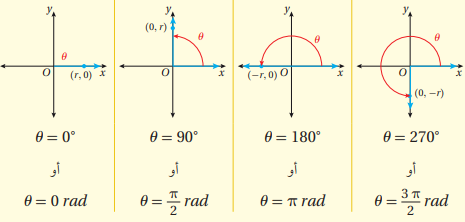 |
ملاحظة:
يمكن إيجاد قيم الاقترانات المثلثية للزواية الربعية عن طريق اختيار نقطة تقع على ضلع انتهاء الزاوية ثم إيجاد الاقتران المثلثي عند تلك النقطة
مثال:
أجد قيمة كل اقتران مثلثي مما يأتي إذا كان معرفاً:
ينطبق ضلع انتهاء الزاوية على المحور x السالب نختار النقطة p (-1,0) على ضلع الانتهاء لأن r=1:
ينطبق ضلع انتهاء الزاوية على محور y الموجب، نختار النقطة p (0,1) على ضلع الانتهاء لأن r=1:
غير معرف=
ينطبق ضلع انتهاء الزاوية على محور x الموجب، نختار النقطة p(1,0) على ضلع الانتهاء، لأن r=1:
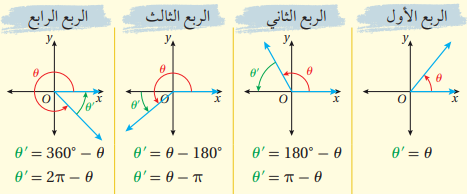
إيجاد قيم الاقترانات المثلثية باستعمال الزاويا المرجعية:
الزاوية المرجعية هي الزاوية الحادة المحصورة بين ضلع انتهاء الزاوية (المرسومة في الوضع القياسي) والمحور x.
 |
ملاحظة:
تستعمل الزوايا المرجعية لإيجاد قيمة الاقترانات المثلثية أما إشارة قيمة الاقتران المثلثي تعتمد على الربع الذي يقع فيه ضلع انتهاء الزاوية .
خطوات إيجاد قيمة الاقترانات المثلثية باستعمال الزاوية المرجعية:
1) نجد قياس الزاوية المرجعية
2) نجد قيمة الاقتران المثلثي للزاوية المرجعية
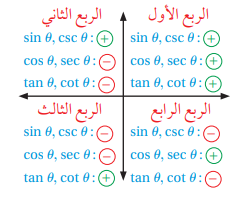
3) نستعمل الربع الذي يقع فيه ضلع انتهاء الزاوية لتحديد إشارة قيمة الاقتران المثلثي والمخطط المجاور يساعدنا على ذلك:
الجدول الآتي يبين قيم بعض الاقترانات المثلثية للزوايا الخاصة :
مثال:
أجد قيمة كل مما يأتي:
يقع ضلع انتهاء الزاوية في الربع الثاني لذا استعمل زاويتها المرجعية
بما أن الزاوية أكبر من الزاوية ، نجد أولاً الزاوية المشتركة مع الزاوية ، التي قياسها موجب، وأقل من :
يقع ضلع انتهاء الزاوية في الربع الأول
بما أن الزاوية سالبة، فاننا نجد أولاً الزاوية المشتركة مع الزاوية ، التي قياسها موجب، وأقل من :
يقع ضلع انتهاء الزاوية في الربع الثالث، لذا نستعمل زاويتها المرجعية:
إيجاد قيم الاقترانات المثلثية إذا علمت قيمة اقتران مثلثي أو أكثر والربع الذي يقع فيه ضلع انتهائها
مثال:
إذا كان حيث فأجد قيمة كل من الاقترانات المثلثية الخمسة المتبقية للزاوية
بما أن موجب و سالب فأن الزاوية تقع في الربع الثالث، وهذا يعني أن اشارة كل من x و y سالبة.
وبما أن نستعمل النقطة (2 , 1) لايجاد قيمة r:
نستعمل , x=1, y=2 لايجاد قيم الاقترانات المثلثية الاخرى:
تطبيقات من الحياة:
تزلج: يمكن حساب الزمن (بالثواني) الذي تستغرقه عملية الانزلاق على منحدر تل يميل عن الافق بزاوية قياسها باستعمال العلاقة: ، حيث d طول المنحدر بالأقدام.
مثال:
أجد الزمن الذي تستغرقه عملية الانزلاق على منحدر طوله 1000ft، وزاوية ميله .
معكوس اقتران الجيب، وجيب التمام، والظل
نعلم أنه يمكن إيجاد الاقتران العكسي لاقتران إذا وفقط إذا كان الاقتران واحد لواحد (كل عنصر في مدى الاقتران يرتبط بعنصر واحد فقط في مجاله).
ملاحظة:
يمكن استعمال اختبار الخط الأفقي للتأكد إذا كان الاقتران واحد لواحد أو ليس كذلك.
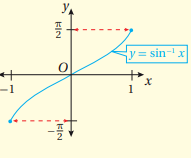
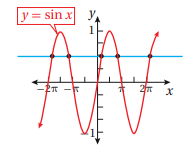
من خلال رسم اقتران الجيب نجد أنه ليس اقتران واحد لواحد بالتالي لا يمكن إيجاد اقتران عكسي له.
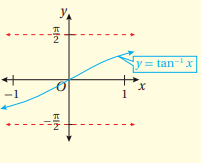
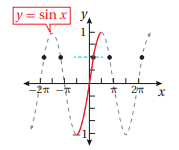
إذا حددنا رسم اقتران الجيب بفترة معينة مثل ، فان الاقتران يصبح واحد لواحد لجميع قيم المدى بالفترة [1,1-]، وبناءً على ذلك يكون الاقتران العكسي لاقتران الجيب هو .
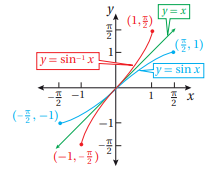
أما التمثيل البياني للاقتران موضح كما بالشكل الآتي:
|
معكوس اقتران الظل اذا وفقط اذا ، حيث: ، المجال: . المدى: .
|
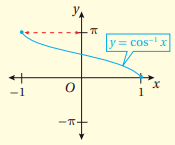
معكوس اقتران جيب التمام اذا وفقط اذا ، حيث: ، المجال: . المدى: .
|
معكوس اقتران الجيب اذا وفقط اذا ، حيث:، و المجال: . المدى: .
|
مثال:
أجد قيمة كل مما يأتي إذا وجدت:
الزاوية التي قيمة جيب التمام لها في الفترة هي ، لذلك فأن:
الزاوية التي قيمة الظل لها في الفترة هي ، لذلك فأن: