رياضيات فصل ثاني

أتحقق من فهمي

ص: 50

أجد قيم الاقترانات المثلثية الستة للزاوية $\theta$ في المثلث المجاور.

$$\begin{gathered} x=\sqrt{49-25}=\sqrt{24} \\ \sin \theta =\frac{5}{7} \\ \cos \theta =\frac{\sqrt{24}}{7} \\ \tan \theta =\frac{5}{\sqrt{24}} \\ csc \theta =\frac{7}{5} \\ sec \theta =\frac{7}{\sqrt{24}} \\ cot \theta =\frac{\sqrt{24}}{5} \end{gathered}$$

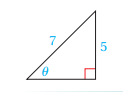
أتحقق من فهمي

ص: 51

تقع النقطة (3-, 1) على ضلع الانتهاء الزاوية $\theta$ المرسومة في الوضع القياسي. أجد قيم الاقترانات المثلثية الستة للزاوية $\theta$.

$$\begin{gathered} r=\sqrt{1+9}=\sqrt{10} \\ \sin \theta =\frac{-3}{\sqrt{10}} \\ \cos \theta =\frac{1}{\sqrt{10}} \\ \tan \theta =-3 \\ csc \theta =\frac{-\sqrt{10}}{3} \\ sec \theta =\sqrt{10} \\ cot \theta =\frac{-1}{3} \end{gathered}$$

أتحقق من فهمي

ص: 53

أجد قيمة كل اقتران مثلثي مما يأتي إذا كان معرفا، والا أكتب عبارة (غير معرف):

$a) \sin \left(3\mathrm{\pi }\right)$

$sin 3\mathrm{\pi }=\frac{0}{1}=0$

$b) \tan \left(90°\right)$

غير معروف$tan 90°=\frac{1}{0}$

$c) \sec \left(-\frac{3\mathrm{\pi }}{2}\right)$

غير معروف$sec \frac{-3\mathrm{\pi }}{2}=\frac{1}{0}$

أتحقق من فهمي

ص: 56

أجد قيمة كل مما يأتي:

$a) \sin \left(210°\right)$

$\sin 210°=-\sin 30°=-0.5$

$b) \cos \left(510°\right)$

$cos 510°=-cos 30°=-\frac{\sqrt{3}}{2}$

$c) \sec \left(5\mathrm{\pi }\right)$

$sec 5\mathrm{\pi }=\mathrm{sec\pi }=-1$

$d) \tan \left(-\frac{2\mathrm{\pi }}{3}\right)$

$\tan -\frac{2\mathrm{\pi }}{3}=-\tan \frac{2\mathrm{\pi }}{3}=\sqrt{3}$

أتحقق من فهمي

ص: 57

إذا كان $sec \theta =2$، حيث $\sin \theta <0$، فأجد قيمة كل من الاقترانات المثلثية الخمسة المتبقية للزاوية $\theta$.

$$\begin{gathered} sin \theta =-\frac{\sqrt{3}}{2} \\ cos \theta =\frac{1}{2} \\ tan \theta =-\sqrt{3} \\ csc \theta =-\frac{2}{\sqrt{3}} \\ cot \theta =-\frac{1}{\sqrt{3}} \end{gathered}$$

أتحقق من فهمي

ص: 57

أجد الزمن الذي تستغرقه عملية الانزلاق على منحدر طوله 3000ft، وزاوية ميله $\frac{\mathrm{\pi }}{4}$، مستعملا العلاقة الواردة في المثال 6.

$t=\frac{\sqrt{d csc \theta }}{4}=\frac{\sqrt{3000 csc {\displaystyle \frac{\mathrm{\pi }}{4}}}}{4}=\frac{\sqrt{3000{\displaystyle \frac{\sqrt{2}}{2}}}}{4}=\frac{10\sqrt{15\sqrt{2}}}{4}\approx 11.51 s$

أتحقق من فهمي

ص: 60

أجد قيمة كل مما يأتي (إن وجدت):

$a) {\sin }^{-1}\frac{1}{\sqrt{2}}$

$si{n}^{-1}\frac{1}{\sqrt{2}}=\frac{\mathrm{\pi }}{4}$

$b) {\cos }^{-1}0$

$co{s}^{-1} 0=\frac{\mathrm{\pi }}{2}$

$c) {\tan }^{-1}\left(-\frac{1}{\sqrt{3}}\right)$

$ta{n}^{-1} \frac{-1}{\sqrt{3}}=-\frac{\mathrm{\pi }}{6}$

أتحقق من فهمي

ص: 61

إذا كانت مساحة القطاع الدائري OAB هي $164 c{m}^2$ في الشكل المجاور، فأجد مساحة $∆OAB$.

$$\begin{gathered} A=\frac{1}{2}{r}^2\theta \\ \frac{1}{2}{\left(20\right)}^2\theta =164 \\ \theta =\frac{41}{50}rad \end{gathered}$$

مساحة المثلث=نصف حاصل ضرب طولي ضلعين فيه بجيب الزاوية المحصورة بينهما.

$\frac{1}{2}{\left(20\right)}^2 sin\frac{41}{50}\approx 146.3 c{m}^2$

أتدرب وأحل المسائل

أجد قيم الاقترانات المثلثية الستة للزاوية $\theta$ في كل مما يأتي:

$$\begin{gathered} x=\sqrt{81-9}=\sqrt{72}=6\sqrt{2} \\ sin \theta =\frac{1}{3} \\ cos \theta =\frac{2\sqrt{2}}{3} \\ tan \theta =\frac{1}{2\sqrt{2}} \\ csc \theta =3 \\ sec \theta =\frac{3}{2\sqrt{2}} \\ cot \theta =2\sqrt{2} \end{gathered}$$

$$\begin{gathered} x=\sqrt{{\left(18\right)}^2-{\left(9\right)}^2}=4\sqrt{14} \\ sin \theta =\frac{2\sqrt{14}}{9} \\ cos \theta =\frac{5}{9} \\ tan \theta =\frac{2\sqrt{14}}{5} \\ csc \theta =\frac{9}{2\sqrt{14}} \\ sec \theta =\frac{9}{5} \\ cot \theta =\frac{5}{2\sqrt{14}} \end{gathered}$$

$$\begin{gathered} x=\sqrt{{\left(26\right)}^2-{\left(14\right)}^2}=4\sqrt{30} \\ sin \theta =\frac{2\sqrt{30}}{13} \\ cos \theta =\frac{7}{13} \\ tan \theta =\frac{2\sqrt{30}}{7} \\ csc \theta =\frac{13}{2\sqrt{30}} \\ sec \theta =\frac{13}{7} \\ cot \theta =\frac{7}{2\sqrt{30}} \end{gathered}$$

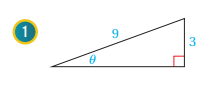
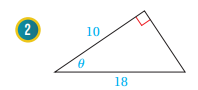
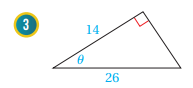
تقع المنطقة المعطاة في كل مما يأتي على ضلع انتهاء الزاوية $\theta$ المرسومة في الوضع القياسي. أجد قيم الاقترانات المثلثية الستة للزاوية $\theta$:

$4) (-12,5)$

$$\begin{gathered} r=\sqrt{144+25}=13 \\ sin \theta =\frac{5}{13} \\ cos \theta =-\frac{12}{13} \\ tan \theta =-\frac{5}{12} \\ csc \theta =\frac{13}{5} \\ sec \theta =-\frac{13}{12} \\ cot \theta =-\frac{12}{5} \end{gathered}$$

$5) (3,-3)$

$$\begin{gathered} r=\sqrt{9+9}=3\sqrt{2} \\ sin \theta =-\frac{1}{\sqrt{2}} \\ cos \theta =\frac{1}{\sqrt{2}} \\ tan \theta =-1 \\ csc \theta =-\sqrt{2} \\ sec \theta =-\sqrt{2} \\ cot \theta =-1 \end{gathered}$$

$6) (-2,-5)$

$$\begin{gathered} r=\sqrt{4+25}=\sqrt{29} \\ sin \theta =-\frac{5}{\sqrt{29}} \\ cos \theta =-\frac{2}{\sqrt{29}} \\ tan \theta =\frac{5}{2} \\ csc \theta =-\frac{\sqrt{29}}{5} \\ sec \theta =-\frac{\sqrt{29}}{2} \\ cot \theta =\frac{2}{5} \end{gathered}$$

$7) (3,7)$

$$\begin{gathered} r=\sqrt{9+49}=\sqrt{58} \\ sin \theta =\frac{7}{\sqrt{58}} \\ cos \theta =\frac{3}{\sqrt{58}} \\ tan \theta =\frac{7}{3} \\ csc \theta =\frac{\sqrt{58}}{7} \\ sec \theta =\frac{\sqrt{58}}{3} \\ cot \theta =\frac{3}{7} \end{gathered}$$

أجد قيمة كل مما يأتي:

$8) sec135°$

$sec 135°=-sec 45°=-\sqrt{2}$

$9) \tan \left(-\frac{3\mathrm{\pi }}{4}\right)$

$tan -\frac{3\mathrm{\pi }}{4}=-tan \frac{3\mathrm{\pi }}{4}=1$

$10) \cot \left(\frac{8\mathrm{\pi }}{3}\right)$

$cot \frac{8\mathrm{\pi }}{3}=cot \frac{2\mathrm{\pi }}{3}=-\frac{1}{\sqrt{3}}$

$11) \cos \frac{7\mathrm{\pi }}{4}$

$cos \frac{7\mathrm{\pi }}{4}=cos \frac{\mathrm{\pi }}{4}=\frac{1}{\sqrt{2}}$

$12) sec\frac{15\mathrm{\pi }}{4}$

$sec \frac{15\mathrm{\pi }}{4}=sec\frac{\mathrm{\pi }}{4}=\sqrt{2}$

$13) \csc \left(-630°\right)$

$csc-630°=csc 90°=1$

$14) \tan 7\mathrm{\pi }$

$tan 7\mathrm{\pi }=\tan \mathrm{\pi }=0$

$15) \sin \left(-\frac{2\mathrm{\pi }}{3}\right)$

$sin -\frac{2\mathrm{\pi }}{3}=-sin \frac{\mathrm{\pi }}{3}=-\frac{\sqrt{3}}{2}$

أجد قيمة كل من الاقترانات المثلثية الخمسة المتبقية للزاوية $\theta$ في كل مما يأتي:

$16) \cos \theta =-\frac{1}{12},\tan \theta >0$

$$\begin{gathered} r=\sqrt{144-49}=\sqrt{95} \\ sin \theta =-\frac{\sqrt{95}}{12} \\ tan \theta =\frac{\sqrt{95}}{7} \\ csc \theta =-\frac{12}{\sqrt{95}} \\ sec \theta =-\frac{12}{7} \\ cot \theta =\frac{7}{\sqrt{95}} \end{gathered}$$

$17) sec \theta =5,\sin \theta <0$

$$\begin{gathered} r=\sqrt{25-1}=\sqrt{24} \\ sin \theta =-\frac{\sqrt{24}}{5} \\ tan \theta =-\sqrt{24} \\ csc\theta =-\frac{5}{\sqrt{24}} \\ cos \theta =\frac{1}{5} \\ cot \theta =-\frac{1}{\sqrt{24}} \end{gathered}$$

$18) cot \theta =\frac{1}{4},\sin \theta <0$

$$\begin{gathered} r=\sqrt{16+1}=\sqrt{17} \\ sin \theta =-\frac{4}{\sqrt{17}} \\ tan \theta =4 \\ csc \theta =-\frac{\sqrt{17}}{4} \\ cos \theta =-\frac{1}{\sqrt{17}} \\ sec \theta =-\sqrt{17} \end{gathered}$$

$19) csc \theta =2,\cos \theta >0$

$$\begin{gathered} r=\sqrt{4-1}=\sqrt{3} \\ sin \theta =\frac{1}{2} \\ tan \theta =\frac{1}{\sqrt{3}} \\ cot \theta =\sqrt{3} \\ cos \theta =\frac{\sqrt{3}}{2} \\ sec \theta \frac{2}{\sqrt{3}} \end{gathered}$$

20) بكرة: يمثل الاقتران: $y=20+\sin \left(10t\right)$ الارتفاع الرأسي بالسنتيمترات لسن بكرة دراجة هوائية بعد t ثانية من بدء حركة الدراجة. أجد الارتفاع الرأسي لسن البكرة بعد 2.5 ثانية من بدء حركة الدراجة.

$y=20+sin 10(2.5)=20+sin 25\approx 19.87 cm$

إذا كان $\cos \frac{\mathrm{\pi }}{12}=0.966$ لأقرب ثلاث منازل عشرية، فأستعمل هذه الحقيقة لإيجاد قيمة كل مما يأتي:

$21) \cos \frac{13\mathrm{\pi }}{12}$

$cos \frac{13\mathrm{\pi }}{12}=-cos \frac{\mathrm{\pi }}{12}=-0.966$

$22) \cos \frac{11\mathrm{\pi }}{12}$

$cos \frac{11\mathrm{\pi }}{12}=-cos \frac{\mathrm{\pi }}{12}=-0.966$

$23) \cos \frac{-\mathrm{\pi }}{12}$

$cos \frac{-\mathrm{\pi }}{12}=cos \frac{\mathrm{\pi }}{12}=0.966$

$24) \cos \frac{23\mathrm{\pi }}{12}$

$cos \frac{23\mathrm{\pi }}{12}=cos \frac{\mathrm{\pi }}{12}=0.966$

أجد قيمة كل مما يأتي:

$25) {\left(\cos \frac{3\mathrm{\pi }}{4}\right)}^2+{\left(\sin \frac{4\mathrm{\pi }}{3}\right)}^2+{\left(\cos \frac{5\mathrm{\pi }}{4}\right)}^2$

${\left(cos \frac{3\mathrm{\pi }}{4}\right)}^2+{\left(sin \frac{4\mathrm{\pi }}{3}\right)}^2+{\left(cos \frac{5\mathrm{\pi }}{4}\right)}^2=\frac{1}{2}+\frac{3}{4}+\frac{1}{2}=\frac{7}{4}$

$26) \sin \frac{\mathrm{\pi }}{3}-\sin \frac{2\mathrm{\pi }}{3}+\mathrm{sin\pi }-\sin \frac{4\mathrm{\pi }}{3}+\sin \frac{5\mathrm{\pi }}{3}-\sin 2\mathrm{\pi }$

   $\frac{\sqrt{3}}{2}- \frac{\sqrt{3}}{2} +0 --\frac{\sqrt{3}}{2}+ -\frac{\sqrt{3}}{2}-0=0$           

يبين الشكل المجاور قطاعاً دائرياً، طول نصف قطره r، وطول قوسه 2r. إذا كانت مساحة الجزء المظلل من القطاع $24 c{m}^2$، فأجد كلا مما يأتي:

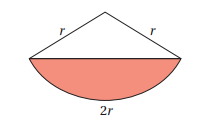
27) طول نصف قطر القطاع.

$$\begin{gathered} l=r\theta \\ 2r=r\theta \\ \theta =2 \\ A=\frac{1}{2}{r}^2\theta -\frac{1}{2}{r}^2 sin \theta \\ 24=\frac{1}{2}{r}^2\left(2\right)-\frac{1}{2}{r}^2 sin 2 \\ r=\sqrt{\frac{48}{2-sin 2}}\approx 6.6 cm \end{gathered}$$

28) محيط الجزء المظلل.

$P=2r+h=2r+2r sin 1\approx 24.3 cm$

أجد قيمة كل مما يأتي:

$29) {\sin }^{-1}\left(-\frac{\sqrt{3}}{2}\right)$

$si{n}^{-1}\left(-\frac{\sqrt{3}}{2}\right)=-\frac{\mathrm{\pi }}{3}$

$30) {\tan }^{-1}\left(-1\right)$

$ta{n}^{-1}\left(-1\right)=-\frac{\mathrm{\pi }}{4}$

$31) {\tan }^{-1}\left(\sqrt{3}\right)$

$ta{n}^{-1}\left(\sqrt{3}\right)=\frac{\mathrm{\pi }}{3}$

$32) {\cos }^{-1}\left(2\right)$

$co{s}^{-1}\left(\frac{\sqrt{2}}{2}\right)=\frac{\mathrm{\pi }}{4}$

مهارات التفكير العليا

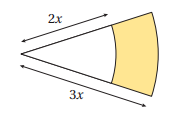
33) تحد: يبين الشكل المجاور قطاعين دائريين ناتجين من دائرتين متحدتين في المركز. اذا كان قياس زاوية القطاعين 0.75، ومساحة الجزء المظلل $30 c{m}^2$، فأجد قيمة x.

$$\begin{gathered} A=\frac{1}{2}{\left(3x\right)}^2(0.75)-\frac{1}{2}{\left(2x\right)}^2(0.75) \\ 30=\frac{27}{8}{x}^2-\frac{3}{2}{x}^2 \\ {x}^2=16 \\ x=4 \end{gathered}$$

تبرير: أثبت كلا مما يأتي، مبررا اجابتي:

$34) \tan 210°+\tan 240°=\frac{4\sqrt{3}}{3}$

$tan 210°+tan 240°=tan 30°+tan 60°=\frac{1}{\sqrt{3}}+\sqrt{3}=\frac{4}{\sqrt{3}}=\frac{4\sqrt{3}}{3}$

$35) \frac{\sin 30°+\sin 60°}{\sin 45°}=\frac{1}{2}(\sqrt{2}+\sqrt{6})$

$\frac{sin 30°+sin 60°}{sin 45°}=\frac{{\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{3}}{2}}}{{\displaystyle \frac{\sqrt{2}}{2}}}=\frac{1+\sqrt{3}}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}+\sqrt{6}}{2}=\frac{1}{2}(\sqrt{2 }+ \sqrt{6})$

36) تحد: يبين الشكل المجاور المقطع العرضي لقطعة خشب أسطوانية الشكل عائمة على الماء. اذا كان نصف قطر المقطع العرضي لقطعة الخشب 30cm، وكانت النقطتان AوB على سطح الماء، وكان ارتفاع أعلى نقطة من هذه القطعة 6cm فوق سطح الماء؛ فأجد النسبة المئوية للجزء من هذه القطعة الواقع تحت سطح الماء.

$$\begin{gathered} cos \theta =\frac{24}{30} \\ \theta \approx 37° \\ 37°\times 2=74°=\frac{37\mathrm{\pi }}{90} \end{gathered}$$

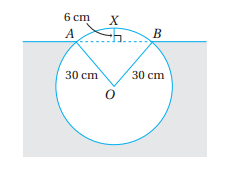
مساحة القطعة العائمة=مساحة القطاع الدائري AOB - مساحة المثلث AOB.

$A=\frac{1}{2}{\left(30\right)}^2\left(\frac{37\mathrm{\pi }}{90}\right)-\frac{1}{2}\left(30\right)\left(30\right) sin \frac{37\mathrm{\pi }}{90}\approx 149 c{m}^2$

مساحة الجزء الواقع تحت سطح الماء= مساحة المقطع العرضي - مساحة القطعة العائمة

$A=\mathrm{\pi }{\left(30\right)}^2-149\approx 2678 c{m}^2$

النسبة المئوية للجزء الواقع تحت سطح الماء تساوي

$\frac{2678}{900\mathrm{\pi }}\times 100\approx 94.7 \raisebox{1ex}{$0$}\!\left/ \!\raisebox{-1ex}{$0$}\right.$

تبرير: يتكون جزيء الأوزون من ثلاث ذرات أكسجين مرتبطة كما في الشكل المجاور:

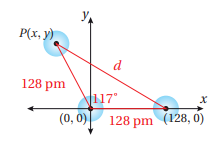
37) أجد احداثيي مركز ذرة الأكسجين P(x,y) الواقع في الربع الثاني، علما بأن الأبعاد على الشكل هي بوحدة البكتومتر $(1pm={10}^{-12}m)$، ثم أبرر اجابتيي.

$$\begin{gathered} \theta =180°-117°=63° \\ sin 63°=\frac{y}{128} \\ y=128 sin 63°\approx 114 \\ cos 63°=\frac{yx}{128} \\ x=128 cos 63°\approx 58 \end{gathered}$$

38) أجد المسافة d بالبكتومتر بين ذرتي الأكسجين غير المرتبطتين.

$d=\sqrt{{(128-58)}^2+{(0-114)}^2}=\sqrt{4900+12996}=\sqrt{17896}\approx 134 pm$

اسئلة كتاب التمارين

أجد قيم الاقترانات المثلثية الستة للزاوية $\theta$ في كل مما يأتي:

$$\begin{gathered} sin \theta =-\frac{3}{5} \\ cos \theta =\frac{4}{5} \\ tan \theta =-\frac{3}{4} \\ csc \theta =-\frac{5}{3} \\ sec \theta =\frac{5}{4} \\ cot \theta =-\frac{4}{3} \end{gathered}$$

$$\begin{gathered} sin \theta =-\frac{4}{5} \\ cos \theta =-\frac{3}{5} \\ tan \theta =\frac{4}{3} \\ csc \theta =-\frac{5}{4} \\ sec \theta =-\frac{5}{3} \\ cot \theta =\frac{3}{4} \end{gathered}$$

$$\begin{gathered} sin \theta =-\frac{3}{5} \\ cos \theta =-\frac{4}{5} \\ tan \theta =\frac{3}{4} \\ csc \theta =-\frac{5}{3} \\ sec \theta =-\frac{5}{4} \\ cot \theta =\frac{4}{3} \end{gathered}$$

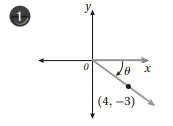
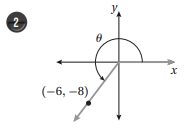
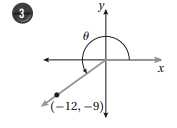
اذا كان: $f\left(x\right)=\sin x,g\left(x\right)=\cos x,h\left(x\right)=2x$، فأجد قيمة كل مما يأتي:

$$\begin{gathered} 4) f(\frac{4\mathrm{\pi }}{3}+\frac{\mathrm{\pi }}{6})+f(\frac{4\mathrm{\pi }}{3})+f(\frac{\mathrm{\pi }}{6}) \\ sin\left(\frac{4\mathrm{\pi }}{3}+\frac{\mathrm{\pi }}{6}\right)+ sin\left(\frac{4\mathrm{\pi }}{3}\right)+ sin\left(\frac{\mathrm{\pi }}{6}\right)= \\ sin\left(\frac{9\mathrm{\pi }}{6}\right)+-\frac{\sqrt{3}}{2}+\frac{1}{2} \\ -1-\frac{\sqrt{3}}{2}+\frac{1}{2} \end{gathered}$$

$\frac{-1-\sqrt{3}}{2}$

$5) (h o g\left)\right(\frac{17\mathrm{\pi }}{3})$

$$\begin{gathered} h\left(g\right(\frac{17\mathrm{\pi }}{3}\left)\right) \\ =2\left(cos\left(\frac{17\mathrm{\pi }}{3}\right)\right) =2\left(\frac{1}{2}\right) = 1 \end{gathered}$$

$6) (h o f\left)\right(\frac{11\mathrm{\pi }}{4})$

$$\begin{gathered} h\left(f\right(\frac{11\mathrm{\pi }}{4}\left)\right)= \\ 2\left(\sin \left(\frac{11\mathrm{\pi }}{4}\right)\right)= \\ 2\left(\frac{1}{\sqrt{2}}\right) \\ =\sqrt{2} \end{gathered}$$

اذا كان $\sin 70°=\cos 20°=0.940$ لأقرب ثلاث منازل عشرية، فأستعمل هذه الحقيقة لايجاد قيمة كل مما يأتي:

$7) \cos 560°$

$-0.940$

$8) \sin 430°$

$0.940$

$9) \sin 470°$

$0.940$

$10) \cos \left(-380°\right)$

$0.940$

يبين الشكل المجاور دائرة مركزها O، وطول نصف قطرها 10cm، اذا كان $\overline{BC}$ مماساً للدائرة طوله 16cm, و DC=AB، فأجد كلا مما يأتي:

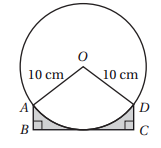
11) $m\angle AOD$ بالراديان.

$106°$

12) مساحة المنطقة المظللة.

$17 c{m}^2$

يبين الشكل المجاور دائرة مركزها O، وطول نصف قطرها 8cm، اذا كان $\overline{TA}$ و $\overline{TB}$ مماسين للدائرة، وكان $m\angle AOT$، فأجد كلا مما يأتي:

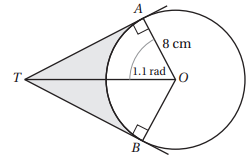
13) طول TA.

$TA=8tan 1.1\approx 15.72 cm$

14) مساحة الجزء المظلل في الشكل.

$55.34 c{m}^2$