حلول أسئلة كتاب الطالب وكتاب التمارين
أسئلة أتحقق من فهمي
أتحقق من فهمي صفحة 73
أَجِدُ مُعادلةَ محورِ التَّماثُلِ، وإحداثِيَّيْ رأسِ الاقترانِ التربيعيِّ
الحل :
| مُعادلةُ محورِ التَّماثُلِ | |
| بتعويض a = 1 , b = 2 |
إذن ، مُعادلةُ محور التماثل هي : x = - 2
| الاقترانُ المُعطى | |
| بتعويضِ x = - 1 |
إذنْ، إحداثِيّا الرأسِ
أتحقق من فهمي صفحة 76
لِكُلِّ قطعٍ مُكافِئٍ ممّا يأتي، أَجِدُ القيمةَ العُظمى أو الصُّغرى والمجالَ والمَدى واتِّجاهَ الفتحة :
في الاقتران f(x) :
بما أنَّ a > 0 فالتمثيلُ البيانيُّ للاقترانِ التربيعيِّ يكونُ مفتوحًا للأعلى، ويكونُ للاقترانِ قيمةٌ صُغرى يمكنُ إيجادُها كالآتي:
الخطوةُ 1 : أَجِدُ الإحداثِيَّ x للرأسِ.
| الإحداثيُّ x للرأسِ | |
| بتعويضِ |
الخطوةُ 2 : أَجِدُ الإحداثِيَّ y للرأسِ.
| الاقترانُ المُعطى | |
| بتعويضِ x = - 0.5 |
إذنْ، القيمةُ الصُّغرى للاقترانِ هِيَ 2.5
المجالُ : جميعُ الأعدادِ الحقيقيَّةِ أوِ الفترةِ
المَدى : { y | y ≥ 2.5 } أوِ الفترةِ
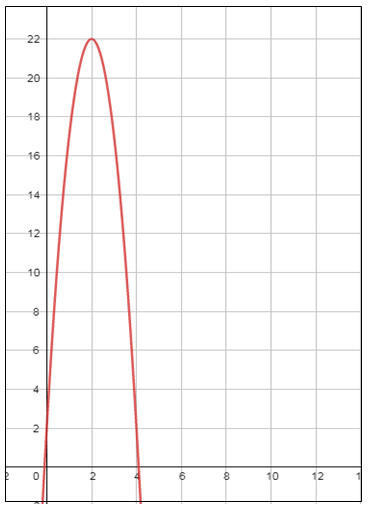
في الاقتران f(x) :
بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للاقترانِ التربيعيِّ يكونُ مفتوحًا للأسفلِ، ويكونُ للاقترانِ قيمةٌ عُظمى يمكنُ إيجادُها كالآتي :
الخطوةُ 1 : أَجِدُ الإحداثِيَّ x للرأسِ.
| الإحداثيُّ x للرأسِ | |
| بتعويض |
الخطوةُ 2 : أَجِدُ الإحداثِيَّ y للرأسِ.
| الاقترانُ المُعطى | |
| بتعويضِ x = 2 |
إذنْ، القيمةُ العظمى للاقترانِ هِيَ 21
المجالُ: جميعُ الأعدادِ الحقيقيَّةِ أوِ الفترةِ
المَدى: أوِ الفترةِ
أتحقق من فهمي صفحة 77
كرةُ قدمٍ: يُمَثِّلُ الاقترانُ ارتفاعَ كرةِ قدمٍ عنْ سطحِ الأرضِ بالأقدامِ، بعدَ t ثانيةً مِنْ ركلِها.
a) أَجِدُ ارتفاعَ الكرةِ بعدَ 3 ثوانٍ مِنْ ركلِها.
الاقتران المُعطى يُمثل الارتفاع ، t تمثل الزمن ، إذن أعوض في الاقتران المعطى t = 3 لأجد الارتفاع بعد 3 ثوانٍ
إذن ، ارتفاع الكرة بعد 3 ثوانٍ من ركلها يساوي 48 قدم .
b) أَجِدُ أقصى ارتفاعٍ تصلُ إليهِ الكرةُ.
تصل الكرة إلى أقصى ارتفاعٍ لها عندَ رأسِ القطعِ المكافئِ؛ لِذا أَجِدُ القيمةَ العُظمى للقطعِ.
الخطوةُ 1 : أَجِدُ الإحداثِيَّ x للرأسِ.
| الإحداثيُّ x للرأسِ | |
| بتعويضِ |
الخطوةُ 2 : أَجِدُ الإحداثِيَّ y للرأسِ.
| الاقترانُ المُعطى | |
| بتعويضِ t = 2 |
إذنْ، أقصى ارتفاعٍ تصلُ إليهِ الكره هو 64 قدم .
أتحقق من فهمي صفحة 78
|
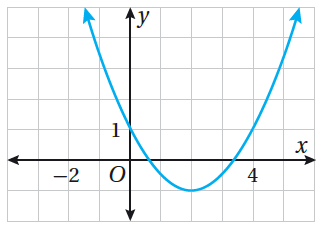
أَجِدُ رأس ومُعادلةَ محورِ التَّماثُلِ، وَالقيمةَ العُظمى أوِ الصُّغرى وَمَجالَ وَمَدى القطعِ المُكافِئ المُمَثَّلِ بيانِيًّا في المُستوى الإحداثِيِّ المُجاورِ: |
 |
الحل :
الخطوةُ 1 : أَجِدُ إحداثِيَّي الرأسِ.
بما أنَّ القطعَ مفتوحٌ للأعلى فالرأسُ يُمَثِّلُ نقطتَهُ الصغرى، وهي ( 1 - , 2).
الخطوةُ 2 : أَجِدُ مُعادلةَ محورِ التَّماثُلِ.
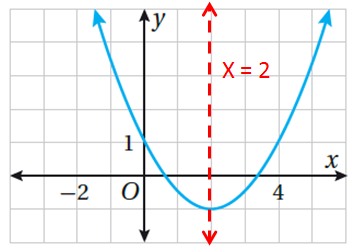
|
بما أنَّ محورَ التَّماثُلِ هُوَ المُستقيمُ الذي يقسِمُ القطعَ المُكافِئَ إلى جزأيْنِ متطابقَيْنِ ، ويقطعُ القطعَ المُكافِئَ في الرأسِ، فإنَّ مُعادلةَ محورِ التَّماثُلِ هِيَ x = 2 |
 |
الخطوةُ 3 : أَجِدُ القيمةَ الصغرى.
بما أنَّ القيمةَ الصغرى هِيَ الإحداثِيُّ y لنقطةِ الرأسِ، فإنَّ القيمةَ الصغرى للاقترانِ هِيَ 1 -
الخطوةُ 4 : أَجِدُ المجالَ وَالمَدى.
المجالُ: جميعُ الأعدادِ الحقيقيَّةِ أوِ الفترةِ
المَدى : أوِ الفترةِ
أتحقق من فهمي صفحة 81
أُمَثلُ الاقتران :
الحل :
الخطوةُ 1 : أُحَدِّدُ اتِّجاهَ فتحةِ القطعِ المُكافِئِ، وَأَجِدُ مُعادلةَ محورِ التَّماثُلِ وإحداثِيَّيِ الرأسِ ، وَأُحَدِّدُ إذا كانَ يُمَثِّلُ نقطةً صُغرى أمْ نقطةً عُظمى.
في الاقترانِ f(x) :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى، وَيُمَثِّلُ الرأسُ نقطتَهُ الصغرى.
• أَجِدُ مُعادلةَ محورِ التَّماثُلِ.
| معادلة محور التماثل | |
| بتعويض |
إذنْ، مُعادلةُ محورِ التَّماثُلِ هِيَ x = 2
• أَجِدُ إحداثِيَّيِ الرأسِ.
| الاقتران المعطى | |
| بتعويض x = 2 |
إذنْ، إحداثِيّا الرأسِ
الخطوةُ 2 : أَجِدُ نقطةَ تقاطعِ الاقترانِ معَ المحورِ y.
لإيجادِ نقطةِ تقاطعِ الاقترانِ معَ المحورِ y، أُعَوِّضُ x = 0 في قاعدةِ الاقترانِ.
| الاقتران المعطى | |
| بتعويض x = 0 |
إذن، نقطة تقاطع الاقتران مع المحور y هي (5- , 0).
الخطوة 3 : أَجِدُ نقطةً أُخرى باختيارِ قيمةٍ لِـ x تقعُ في الجانبِ الذي يقعُ فيهِ المقطعُ y يمين محور التماثُل أو يسارَهُ.
أختارُ x = 1
| الاقتران المعطى | |
| بتعويض x = 1 |
إذنْ، النقطة الأُخرى هي (8- , 1).
|
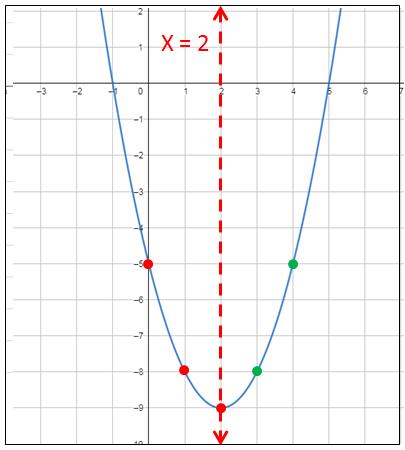
الخطوة 4 : أُمَثِّلُ النقاطَ في المُستوى الإحداثيِّ. أُمَثِّلُ رأسَ القطعِ والنقطتَيْنِ اللتَيْنِ أوجدتُهما مِنَ الخُطوتَيْنِ 2 وَ 3، وَهُما (8- , 0) وَ ( 9- , 2)، ثمَّ أستعملُ التَّماثُلَ لأعكِسَ النقطتَيْنِ (8- , 0) وَ (9- , 2) حولَ محورِ التماثل ؛ لإيجاد نقطتين أُخرَيَيْنِ على التمثيل البيانِيّ. الخطوة 5 : أصِلُ بين النقاطِ بِمُنحنًى أملَس. |
 |
أسئلة أتدرب وأحل المسائل
أَجِدُ رأسَ ومُعادلةَ محورِ التَّماثُلِ، والقيمةَ العُظمى أوِ الصُّغرى وَمَجالَ وَمَدى الاقتراناتِ التربيعيَّةِ الآتيةِ :
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 0
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 0
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ، وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 5
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 3
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 5-
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 8-
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ، وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 8.5
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ، وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 37
المجالُ :
المَدى : أو الفترة
معادلة محور التماثل :
، إذن الرأس :
بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ، وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 3-
المجالُ :
المَدى : أو الفترة
أَجِدُ رأسَ ومُعادلةَ محورِ التَّماثُلِ والقيمةَ العُظمى أوِ الصُّغرى ومجالَ وَمَدى كلٍّ مِنَ القطوعِ المُكافِئةِ الآتيةِ :
|
القطعَ مفتوحٌ للأعلى، إذن له قيمة صغرى الرأس: ( 2 - , 1) ، إذن القيمة الصغرى هي الإحداثي y لنقطة الرأس وهي 2- محور التماثل : x = 1 المجال : المدى : |
 |
|
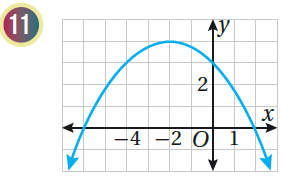
القطعَ مفتوحٌ للأسفل ، إذن له قيمة عظمى الرأس : (4 , 2-) ، إذن القيمة العظمى هي الإحداثي y لنقطة الرأس وهي 4 محور التماثل : x = - 2 المجال : المدى : |
 |
|
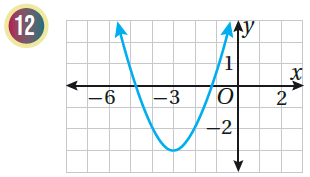
القطعَ مفتوحٌ للأعلى ، إذن له قيمة صغرى الرأس : (3 - , 3-) ، إذن القيمة الصغرى هي الإحداثي y لنقطة الرأس وهي 3- محور التماثل : x = -3 المجال : المدى : |
 |
أُمثل كُلًّ من الاقترانات الآتية بيانيًّا :
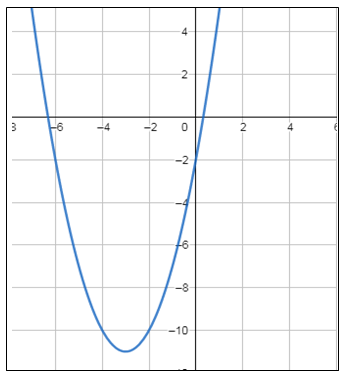
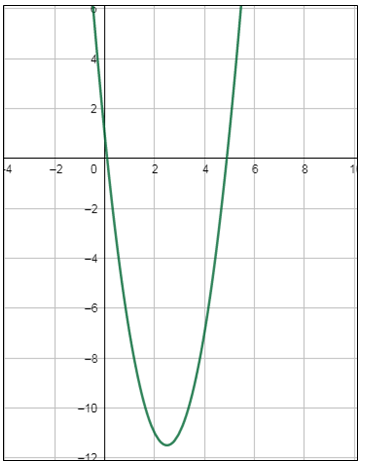
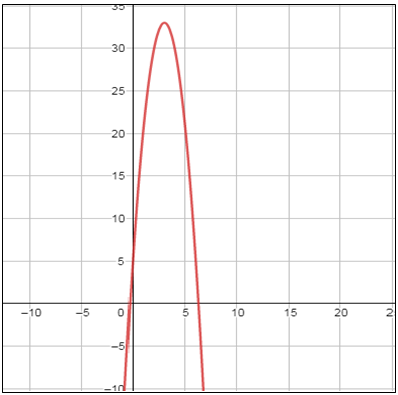
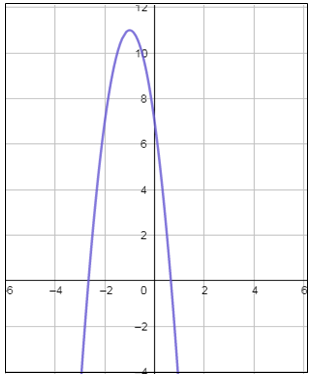
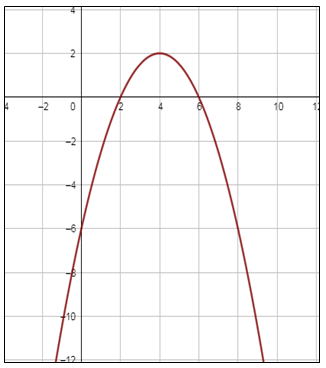
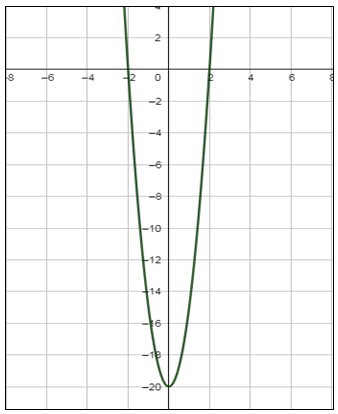
|
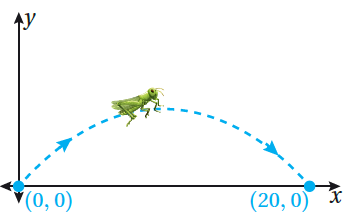
19) حشراتٌ: يُمَثِّلُ الاقترانُ ارتفاعَ جندبٍ بالسنتيمترٍ فوقَ سطحِ الأرضِ عندَ قفزِهِ؛ حيثُ x المسافةُ الأفقيَّةُ مِنْ نقطةِ القفزِ. أَجِدُ أقصَى ارتفاعٍ يمكنُ أنْ يَصِلَ إليهِ الجندبُ. |
 |
الحل :
أجد القيمة العظمى للاقتران
معادلة محور التماثل :
القيمة العظمى : ، إذن أقصى ارتفاع يصل إليه الجندب هي
رياضةٌ: يُمَثِّلُ الاقترانُ ارتفاعَ كرةِ مضربٍ بالأمتارِ فوقَ سطحِ الأرضِ، بعدَ t ثانيةً مِنْ ضربِ سميرٍ لها.
20) أَجِدُ ارتفاعَ الكرةِ لحظةَ ضربِ سميرٍ لها.
21) أَجِدُ أقصَى ارتفاعٍ يمكنُ أنْ تَصِلَ إليهِ الكرةُ.
مهاراتُ التفكيرِ العُليا
22) مسألةٌ مفتوحةٌ: أكتبُ قاعدةَ اقترانٍ تربيعيٍّ مُعادلةُ محورِ تماثُلِهِ x = - 2
إجابة محتملة :
23) أكتشفُ الخطأَ : حاولَ هشامٌ وَمَلَكُ إيجادَ مُعادلةِ محورِ التَّماثُلِ للقطعِ المُكافِئِ ، فكانَتْ إجابَتاهُما كالآتي. أيُّهُما إجابتُهُ صحيحةٌ؟ أُبَرِّرُ إجابتي.

الإجابة :
إجابة ملك صحيحة ؛ لأن b = - 16 مع السالب الموجودة في صيغة معادلة محور التماثل تصبح 16 مقسومًا على 4 - فتكون المعادلة x = - 4
| 24) تَحَدٍّ: أَجِدُ قاعدةَ الاقترانِ المُمَثَّلِ بيانيًّا في الشكلِ المُجاورِ. | 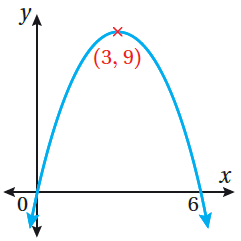 |
الحل :
من النقاط الثلاث المعلومة على التمثيل البياني واستخدام الصورة القياسية للاقتران التربيعي
الصورة القياسية للاقتران التربيعي :
أعوض النقطة (0 ، 0) في الاقتران :
أعوض النقطة (0 ، 6) في الاقتران :
أعوض النقطة (9 ، 3) في الاقتران :
بحل المعادلتين 1 ، 2 بالحذف ينتج
بتعويض a = -1 في أحد المعادليتن ينتج
إذن الاقتران التربيعي هو :
أسئلة كتاب التمارين
أَجِدُ رأسَ ومعادلةَ محورِ التَّماثُلِ، والقيمةَ العُظمى أوِ الصُّغرى وَمَجالَ وَمَدى كلٍّ مِنَ الاقتراناتِ التربيعيَّةِ الآتيةِ، ثمَّ أُمَثِّلُهُ بيانِيًّا:
|
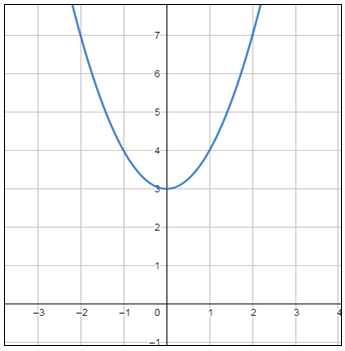
معادلة محور التماثل : ، إذن الرأس (3 ، 0) بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 3 المجال : المدى : |
 |
|
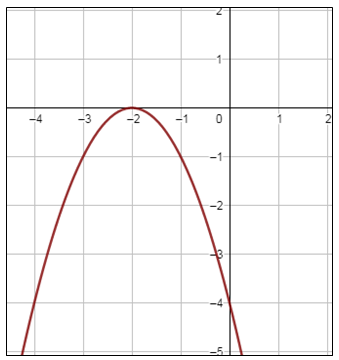
معادلة محور التماثل : ، إذن الرأس (0 ، 2-) بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 0 المجال : المدى : |
 |
|
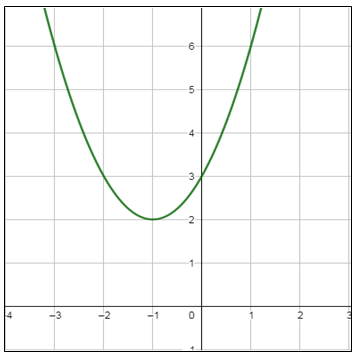
معادلة محور التماثل : ، إذن الرأس (2 ، 1-) بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 2 المجال : المدى : |
 |
|
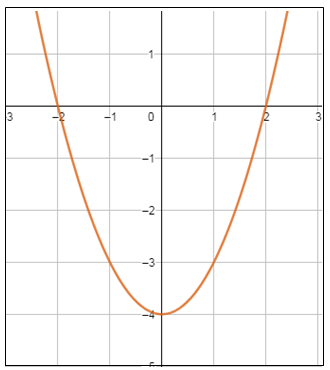
معادلة محور التماثل : ، إذن الرأس (4- ، 0)
بما أنَّ a > 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأعلى ، وقيمته الصغرى هي الإحداثي y لنقطة الرأس وهي 4- المجال : المدى : |
 |
|
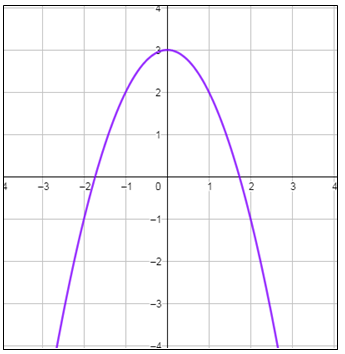
معادلة محور التماثل : ، إذن الرأس (3 ، 0) بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 3 المجال : المدى :
|
 |
|
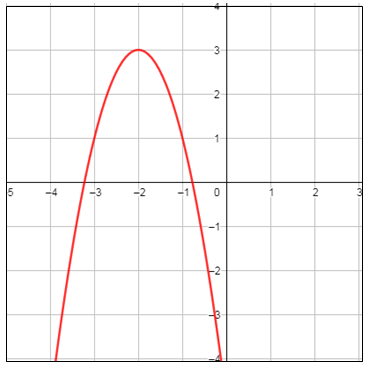
معادلة محور التماثل : ، إذن الرأس (3 ، 2-) بما أنَّ a < 0 ، فالتمثيلُ البيانيُّ للقطعِ المُكافِئِ يكونُ مفتوحًا للأسفلِ وقيمته العظمى هي الإحداثي y لنقطة الرأس وهي 3 المجال : المدى : |
 |
أَصِلُ الاقترانَ بتمثيلِهِ البيانِيِّ في كلٍّ ممّا يأتي:
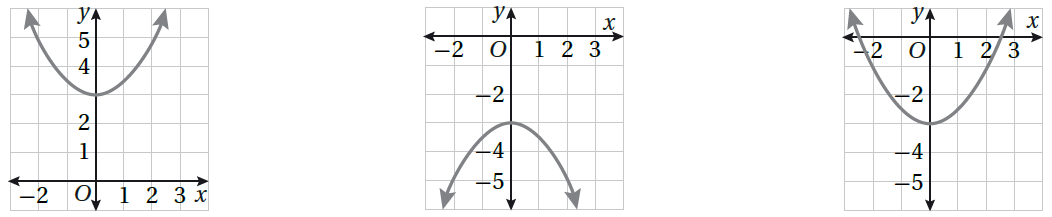
الحل :
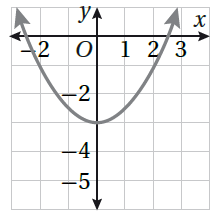 |
|
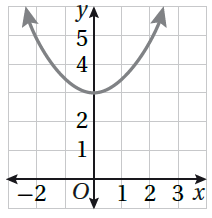 |
|
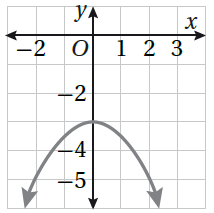 |
رياضةٌ: يُمَثِّلُ الاقترانُ ارتفاعَ رمحٍ بالمترِ عَنْ سطحِ الأرضِ، بعدَ t ثانيةً مِنْ رميِهِ.
10) أَجِدُ مقطعَ المُنحنى مِنْ محورِ y ، وَأُفَسِّرُ معناهُ في سياقِ المسألةِ.
الحل :
لإيجادِ نقطةِ تقاطعِ الاقترانِ معَ المحورِ y، أُعَوِّضُ t = 0 في قاعدةِ الاقترانِ ؛ وهذا يعني إيجاد الارتفاع لحظة إطلاق الرمح .
11) أَجِدُ القيمةَ العُظمى للاقترانِ، وَأُفَسِّرُ معناها في سياقِ المسألةِ.
الحل :
معادلة محور التماثل :
، إذن الرأس (22 ، 2) والقيمة العظمى = m 22 ، وهي تمثل أقصى ارتفاع وصل إليه الرمح .
12) أُمَثِّلُ الاقترانَ h بيانِيًّا.
الحل :