رياضيات 10 فصل ثاني

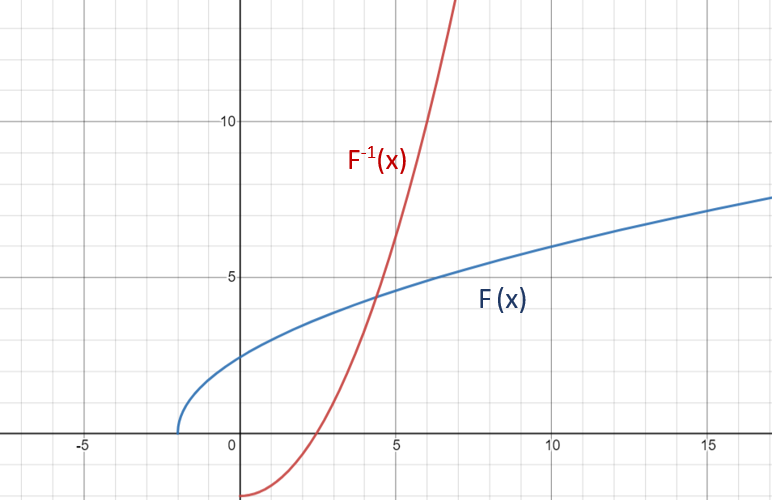
أتحقق من فهمي  صفحة 33

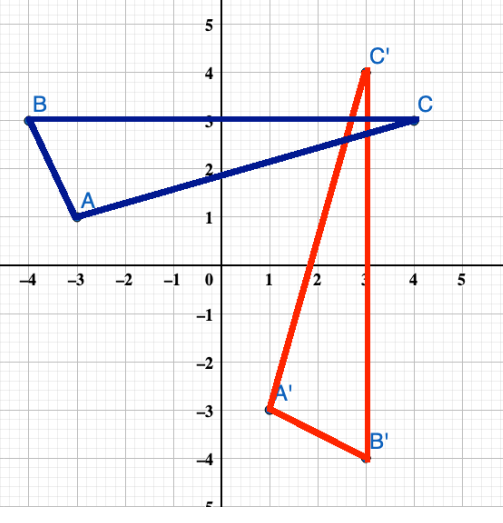
تمثل الأزواج المرتبة للعلاقة $\left\{\right(-3,1),(-4,3),(4,3\left)\right\}$ إحداثيات رؤوس المثلث ABC. أجد العلاقة العكسية ، ثم أمثل بيانيا العلاقة والعلاقة العكسية على المستوى الإحداثي نفسه.

الحل:

العلاقة العكسية :

$\left\{\right(1,-3),(3,-4),(3,4\left)\right\}$

 

---

أتحقق من فهمي  صفحة 36

 

أجد الاقتران العكسي لكل من الاقترانين الآتيين : 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

أتحقق من فهمي  صفحة 37

 

أثبت أن كلا من الاقترانين f(x) = 4x -8 و $g\left(x\right) = \frac{x}{4 }+2$  هو اقتران عكسي للآخر.

الحل:

 

---

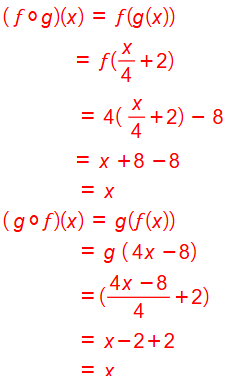
أتحقق من فهمي  صفحة 38

 

أجد مجال $g\left(x\right) = \sqrt{3x +12} - 2$ومداه ، ثم أجد الاقتران العكسي له.

الحل :

 

 

---

أتحقق من فهمي  صفحة 39

يرتبط محيط الرأس C  للطفل بطوله H ( كلا القياسين بالسنتيمتر) عن طريق الاقتران :

 :H(C) = 2.15 C - 26.75 

a) أكتب اقترانا يعبر عن محيط الرأس C بدلالة طول الطفل H .

الحل :

H = 2.15C -26.75

 

H +26.75 = 2.15C

 

$\frac{H+26.75}{2.15}=C$

 

b) أجد محيط رأس طفل طوله  66cm 

الحل:

$C\left(H\right)=\frac{H+26.75}{2.15}$

 

$C\left(66\right)=\frac{66+26.75}{2.15}\Rightarrow C\left(66\right)\approx 43.13$

---

 

أتدرب و أحل المسائل 

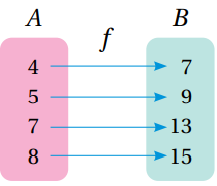
أحدد الاقتران الذي له اقتران عكسي في كل مما يأتي ، مبررا إجابتي ، ثم أكتب الاقتران العكسي ( إن وجد) :

1. $f=\left\{\right(2,6),(-3,6),(4,9),(1,10\left)\right\}$ 

الحل :

ليس له اقتران عكسي لأنه ليس واحد لواحد حيث 2 و 3- مرتبطين مع 6

 

 

2. $h=\left\{(0,0),(1,1),(2,16),(3,81)\right\}$

الحل :

له اقتران عكسي لأنه واحد لواحد

$h^{-1}=\left\{( 0,0),(1,1),(16,2),(81,3)\right\}$

 

 

3.

الحل :

له اقتران عكسي لأنه اقتران واحد لواحد

$f^{-1}=\left\{(7,4),(9,5),(13,7),(15,8)\right\}$

 

 

 

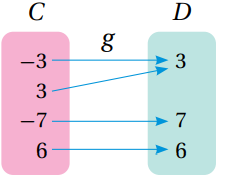
4.

الحل:

ليس له اقتران عكسي لأنه ليس اقتران واحد لواحد حيث 3 و 3- مرتبطين مع 3

---

 

إذا كان $f\left(x\right)=3(\frac{x}{2}+4)$، فأجد قيمة كل مما يأتي :

5. f( -2)

الحل

$f(-2)=3(\frac{-2}{2}+4)=3(-1+4)=3\left(3\right)=9$

 

6. f(4)

الحل

$f\left(4\right)=3(\frac{4}{2}+4)=3(2+4)=3\left(6\right)=18$

 

7. f ^-1(9)

الحل

$y=3(\frac{x}{2}+4)\Rightarrow y=\frac{3}{2}x+12$

 

$y-12=\frac{3}{2}x\Rightarrow 2y-24=3x$

 

$x=\frac{2y-24}{3}$

 

$f^{-1}\left(x\right)=\frac{2x-24}{3}$

 

$f^{-1}\left(9\right)=\frac{2\left(9\right)-24}{3}= \frac{18-24}{3}=\frac{-6}{3}=-2$

 

8. f ^-1(18)

الحل

$f^{-1}\left(x\right)=\frac{2x-24}{3}$

 

$f^{-1}\left(18\right)=\frac{2\left(18\right)-24}{3}=\frac{36 -24}{3}=\frac{12}{3}=4$

---

 

أجد الاقتران العكسي لكل من الاقترانات الآتية :

 f(x) =x +7 (9

الحل:

y = x +7

y-7 = x

f^-1(x) = x - 7

 

 f(x) = 8x (10

الحل

$y=8x\Rightarrow \frac{y}{x}=x\Rightarrow f^{-1}\left(x\right)=\frac{x}{8}$

 

11. $f\left(x\right) = \frac{x}{2}+6$

الحل

$y=\frac{x}{2}+6\Rightarrow y-6=\frac{x}{2}$

 

$2y-12=x\Rightarrow f^{-1}\left(x\right)=2x-12$

 

$12. f\left(x\right)= \frac{3x -6}{5}$ =

الحل

$y=\frac{3x-6}{5}\Rightarrow 5y=3x-6$

 

$5y+6=3x\Rightarrow x=\frac{5y+6}{3}$

 

$f^{-1} \left(x\right)=\frac{5x+6}{3}$

 

13. f(x) = 4x³

^الحل

^{$y=4x^3$}

^{$\frac{y}{4}=x^3\Rightarrow \sqrt[3]{\frac{y}{4} }=x$}

^{$f^{-1}\left(x\right)=\sqrt[3]{\frac{x}{4}}$}

 

$14. g\left(x\right) =4+\sqrt[]{6-3x }, x\le 2$

الحل

$y=4+\sqrt[]{6-3x}$

$y-4 =\sqrt[]{6-3x}$

${(y-4)}^2 =6-3x\Rightarrow 3x=6-{(y-4)}^2$

$x=\frac{6-{(y-4)}^2}{3}\Rightarrow f^{-1}\left(x\right)= \frac{6- {( x-4)}^2}{3}$

 

 

15. $g\left(x\right) = \frac{8-3x}{5x} , x\ne 0$ 

 

 

$16. j\left(x\right) ={(x -2)}^2 +4 , x\ge 2$

$y= {(x-2)}^2+4 \Rightarrow y-4= {(x-2)}^2$

$\sqrt[]{y-4}=x-2\Rightarrow \sqrt[]{y-4}+2=x$

$f^{-1}\left(x\right)=\sqrt[]{x-4}+2$

---

 

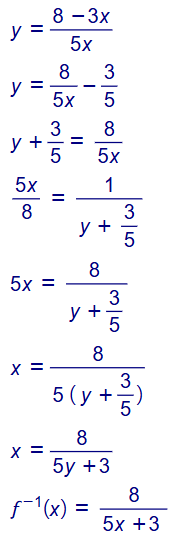
17. أثبت أن كلا من الاقترانين f(x) , g(x)  هو اقتران عكسي للآخر :

$f\left(x\right)= {(x+3)}^2 , x\ge -3 , g\left(x\right)=-3 +\sqrt[]{x-2}, x\ge 2$

 

 

---

 

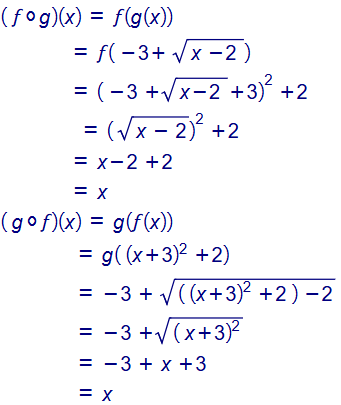
18.  أثبت أن $f\left(x\right)=\frac{x}{x-1 } , x \ne 1$هو اقتران عكسي لنفسه .

$(f\circ f)\left(x\right)=f\left(f\right(x\left)\right)=f\left(\frac{x}{x -1}\right)$

 

$= \frac{\frac{x}{x - 1}}{\frac{x}{x-1}-1}=\frac{\frac{x}{x-1}}{\frac{x}{x -1}- \frac{x -1}{x-1}}$

 

$=\frac{\frac{x}{x-1}}{\frac{x-x+1}{x-1}}=\left(\frac{x}{x-1 }\right)\left(\frac{x-1}{1}\right)=x$

 

---

 

19.  صناعة إذا كان C(x)  يمثل التكلفة C  بالدينار لإنتاج x وحدة من مصابيح الإنارة ، فماذا يمثل المقدار  C ^-1 ( 23000) ؟ 

يمثل عدد المصابيح المنتجة إذا كانت الكلفة 23000

---

 

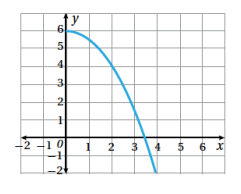
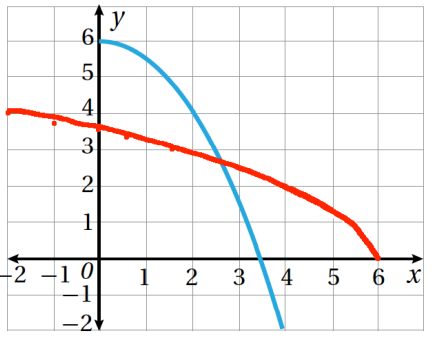
20. أرسم منحنى الاقتران العكسي للاقتران f المجاور في المستوى الإحداثي نفسه، معينا المجال و المدى لكل من f  و f^-1 .

الحل :

$\mathrm{مجال} f \mathrm{هو} [4,0]$

$\mathrm{مدى} f \mathrm{هو} [6,2-]$

$\mathrm{مجال}{ }^{1-}f \mathrm{هو} [6,2-]$

$\mathrm{مدى}{ }^{1-}f \mathrm{هو} [4,0]$

 

---

21. أجد الاقتران العكسي للاقتران :

  $-3 \le x\le 1$, f(x) = x² -2x +5 , ثم أمثل f(x) و f^-1 (x) بيانيا في المستوى الإحداثي نفسه .

 

( إرشاد : أكتب f(x)  بصورة  ${(x+b)}^2+c$  باستعمال إكمال المربع )

 

 

---

 

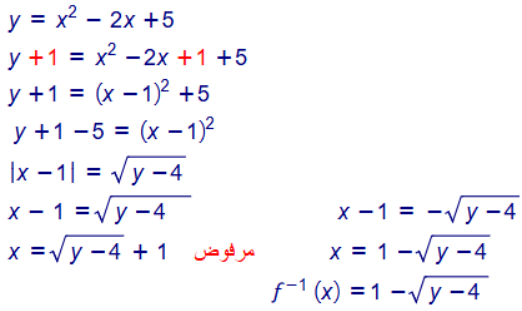
22. كيمياء : في دورق 100ml من أحد المحاليل ، منها 25ml من حامض الهيدروكلوريك . إذا أضيف إلى الدورق  n ml من محلول مشابه ، تركيز الحامض فيه 60% ، فإن تركيز الحامض في الدورق يعطى بالاقتران  $C\left(n\right)=\frac{25+0.6n}{100+n}$. أعبر عن n بصورة اقتران بدلالة التركيز C، ثم أجد عدد المليمترات n التي يجب إضافتها ليصبح تركيز الحامض في الدورق 50% .

$y=\frac{25+0.6n}{100+ n}$

 

$0.6n-ny=100y-25\Rightarrow n(0.6-y)100y-25$

 

$n=\frac{100y-25}{0.6-y}\Rightarrow n\left(C\right)=\frac{100C-25}{0.6-C}$

 

$n(0.5)=\frac{100(0.5) -25}{0.6-(0.5)}=\frac{25}{0.1}=250$

 

---

 

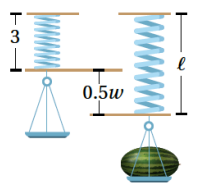
23. أحل المسألأة الواردة في بداية الدرس.

يستعمل الاقتران  L = 0.5w +3  لإيجاد طول الزنبرك L  بالسنتميترات في الميزان الزنبركي عند قياس كتلة الجسم w بالكيلوغرام. هل يمكن إيجاد اقتران آخر يستعمل لإيجاد كتلة الجسم إذا علم طول الزنبرك ؟

 

 

 

نعم فالاقتران العكسي يبين كتلة الجسم بدلالة طول الزنبرك ، وهو

w = 2( L -3)

حيث

L -3 = 0.5 y 

y = 2( L -3)

---

 

24. تعطى مساحة السطح الكلية A للأسطوانة التي نصف قطر قاعدتها r ، وارتفاعها 40cm بالاقتران.

$A\left(r\right)=2{\mathrm{\pi r}}^2+80\mathrm{\pi r}$. أعبر عن نصف القطر r بصورة اقتران بدلالة المساحة A ، ثم أجد طول نصف قطر قاعدة أسطوانة مساحة سطحها الكلية  2000cm².

 

 

---

 

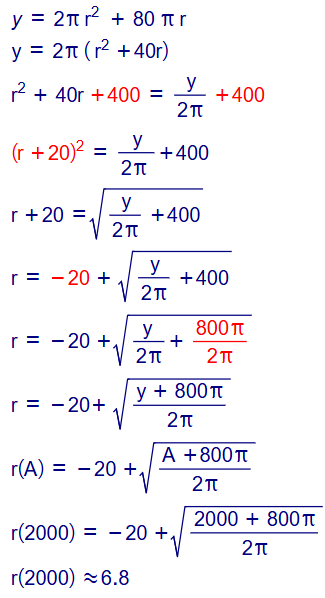
25. أجد الاقتران العكسي للاقتران $f\left(x\right)= \sqrt[3]{x}$ثم أمثل f(x) , f^-1(x) بيانيا في المستوى الإحداثي نفسه .

 

$y=\sqrt[3]{x}\Rightarrow y^3=x\Rightarrow f^{-1}\left(x\right)=x^3$

 

---

 

مهارات التفكير العليا

26. تبرير : إذا كان f(x)  اقتران عكسي ، وكان له صفر عندما x =4 ، فما الذي يمكن استناجه عن منحنى  f^-1 (x) ؟

منحنى الاقتران f ^-1 (x)  يمر بالنقطة ( 4 , 0 )

---

 

27. مسألة مفتوحة : أكتب قاعدة اقتران واحد لواحد والاقتران العكسي له، ثم أثبت أن كلا منهما اقتران عكسي للآخر.

 

 

---

 

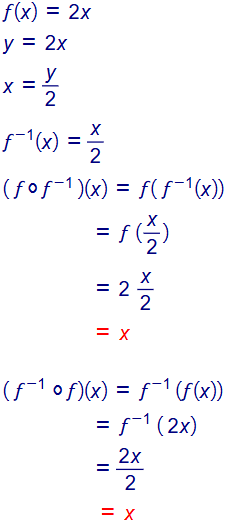
28. تحد : إذا كان $f\left(x\right)=x^2+3$  و $g\left(x\right)=5x-1$  و $x>0$ فأحل المعادلة : $(f\circ g)\left(x\right)=g^{-1}\left(34\right)$

 

 

---

 

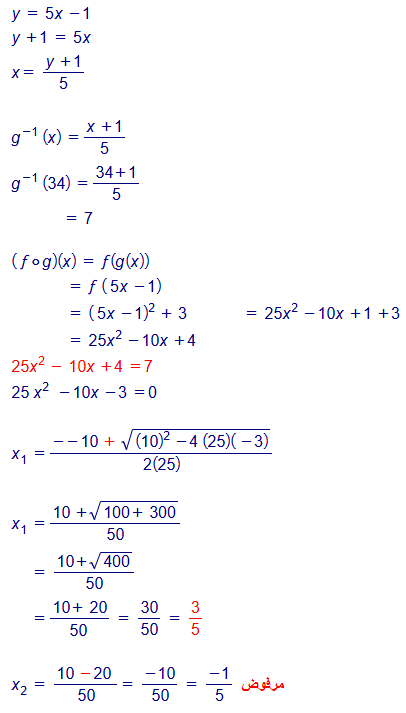
كتاب التمارين 

 

إذا كان $g\left(x\right)=80-\frac{100}{1+x }$ ، فأجد كلا مما يأتي :

1. g(9) =

$$\begin{gathered} g( 9) = 80 - \frac{100}{1+9} \\ = 80 - \frac{100}{10} \\ = 80 - 10 \\ = 70 \end{gathered}$$

2. g(4) =

$$\begin{gathered} g\left(4\right) = 80 -\frac{100}{5} \\ = 80 -20 \\ = 60 \end{gathered}$$

3. g^-1 (70) =

$$\begin{gathered} y = 80 - \frac{100}{1 +x } \\ y -80 = -\frac{100}{1+ x} \\ ( 1+x)(y -80) = -100 \\ 1+x = \frac{-100}{y -80} \\ x = -1 - \frac{100}{y -80} \\ {g}^{-1}\left(x\right) = -1 -\frac{100}{x-80} \\ {g}^{-1} ( 70) = -1 -\frac{100}{-10} \\ = -1 +10 \\ = 9 \end{gathered}$$

4. g^-1 (60) =

$$\begin{gathered} g^{-1} \left(60\right) = -1 -\frac{100}{-20} \\ = -1 - (-5) \\ = -1 +5 \\ = 4 \end{gathered}$$

---

5. إذا كان f(x) اقتران واحد لواحد ، و f(3) = 8  ، فماذا يستنتج من هذه المعطيات ؟

أن f^-1 (8) = 3 

---

6. إذا كان f(x)  يمثل عدد الوحدات المنتجة في x  ساعة عمل لمنتج معين ، فماذا يمثل المقدار  f^-1 ( 2540) ؟

$$\begin{gathered} f\left(x\right) \to \mathrm{الوحدات} \mathrm{عدد} \\ {f}^{-1} ( 2540) \to \mathrm{وحدة} 2540 \mathrm{إنتاج} \mathrm{يتم} \mathrm{خلالها} \mathrm{من} \mathrm{التي} \mathrm{العمل} \mathrm{ساعات} \end{gathered}$$

---

أجد الاقتران العكسي f^-1(x) لكل مما يأتي ، محددا مجـاله و مـداه :

7. f(x) = 3x -5

$$\begin{gathered} y = 3x - 5 \\ x = \frac{y +5}{3} \\ \frac{y +5}{3}= x \Rightarrow f^{-1} \left(x\right) =\frac{x +5}{3} \end{gathered}$$

مجاله : جميع الأعداد الحقيقية 

مداه : جميع الأعداد الحقيقية

8. f(x) = 4 -7x

$$\begin{gathered} y = 4 -7x \\ \frac{y - 4 }{-7}= x \Rightarrow x = -\frac{y -4}{7} \\ {f}^{-1} \left(x\right) = \frac{4 - x}{7} \end{gathered}$$

مجاله : جميع الأعداد الحقيقية 

مداه : جميع الأعداد الحقيقية

$9. f\left(x\right) =x^2 +3 , x\ge 0$

$\sqrt{y -3 } = x \Rightarrow \mathbf{ }{\mathit{f}}^{\mathbf{-}\mathbf{1}}\mathbf{ }\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\sqrt{\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{3}}$

مجاله $[ 3 ,\infty )$

 مداه $[ 0 , \infty )$

$10. f\left(x\right) 5 -9x^2 , x\ge 0$

$x = \sqrt{\frac{y -5}{-9} } \mathbf{\Rightarrow }\mathbf{ }{\mathit{f}}^{\mathbf{-}\mathbf{1}\mathbf{ }}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\sqrt{\mathbf{ }\mathbf{-}\mathbf{ }\frac{\mathbf{(}\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{5}\mathbf{)}}{\mathbf{9}}}$

مجاله $( -\infty ,5]$

مداه   $[0 , \infty )$

$11. f\left(x\right) =\frac{x}{2x +6}$

$$\begin{gathered} y = \frac{x }{2x +6} \\ y ( 2x +6) = x \\ 2xy +6y = x \\ x -2xy = 6y \\ x( 1 -2y ) = 6y \\ x =\frac{6y }{1 - 2y } \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}}\mathbf{ }\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{6}\mathbf{x}}{\mathbf{1}\mathbf{ }\mathbf{-}\mathbf{2}\mathbf{x}\mathbf{ }} \end{gathered}$$

مجاله : جميع الأعداد الحقيقية ما عدا $\frac{1}{2 }$

مداه : مجموعة الأعداد الحقيقية ما عدا 3-

$12. f\left(x\right) = \frac{x}{8 -4x}$

$$\begin{gathered} y = \frac{x }{8 -4x} \\ 8 y -4xy = x \\ 8y = x( 4y +1) \\ x = \frac{8y }{4y +1} \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}\mathbf{ }}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{8}\mathbf{x}\mathbf{ }}{\mathbf{4}\mathbf{x}\mathbf{ }\mathbf{+}\mathbf{1}\mathbf{ }} \end{gathered}$$

مجاله مجموعة الأعداد الحقيقية ما عدا $-\frac{1}{4}$

مداه مجموعة الأعداد الحقيقية ما عدا  2

$13. f\left(x\right) =\sqrt{2x -1} +3$

$$\begin{gathered} y = \sqrt{2x -1 } + 3 \\ y -3 = \sqrt{2x -1} \\ {( y-3)}^2 = 2x -1 \\ x = \frac{{(y -3)}^2 +1}{2} \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}\mathbf{ }}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{3}\mathbf{)}}^{\mathbf{2}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{1}}{\mathbf{2}} \end{gathered}$$

مجاله جميع الأعداد الحقيقية$x\ge 3$

مداه $[ \frac{1}{2} , \infty )$

$14. f\left(x\right) =\sqrt{3x +2} -5$

$$\begin{gathered} y = \sqrt{3x +2 } - 5 \\ \frac{{( y+5)}^{2 } -2}{3} = x \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}}\mathbf{ }\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{{\mathbf{(}\mathbf{x}\mathbf{+}\mathbf{5}\mathbf{)}}^{\mathbf{2}}\mathbf{ }\mathbf{-}\mathbf{2}}{\mathbf{3}} \end{gathered}$$

مجاله مجموعة الأعداد الحقيقية$x\ge -5$

المدى $[ -\frac{2}{3} ,\infty )$

$15. f\left(x\right) = \sqrt[3]{3x - 2} - 1$

$$\begin{gathered} y = \sqrt[3]{3x -2} - 1 \\ \frac{{( y+1)}^3 +2}{3} = x \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}\mathbf{ }}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{+}\mathbf{1}\mathbf{)}}^{\mathbf{3}\mathbf{ }}\mathbf{ }\mathbf{+}\mathbf{2}}{\mathbf{3}} \end{gathered}$$

مجاله مجموعة الأعداد الحقيقية

المدى مجموعة الأعداد الحقيقية

$16.f\left(x\right) =\sqrt[3]{3 - 4x } +1$

$$\begin{gathered} y = \sqrt[3]{3 -4x +1} \\ \frac{{( y -1)}^3 - 3}{-4} = x \\ {\mathit{f}}^{\mathbf{-}\mathbf{1}\mathbf{ }}\mathbf{\left(}\mathit{x}\mathbf{\right)}\mathbf{ }\mathbf{=}\mathbf{ }\frac{\mathbf{3}\mathbf{ }\mathbf{-}\mathbf{ }{\mathbf{(}\mathbf{ }\mathbf{x}\mathbf{ }\mathbf{-}\mathbf{1}\mathbf{)}}^{\mathbf{3}}}{\mathbf{4}} \end{gathered}$$

مجاله مجموعة الأعداد الحقيقية

المدى مجموعة الأعداد الحقيقية

---

 أمثل إذا كان كل من الاقترانين h(x) , f(x)  اقترانا عكسيًا للآخر أم لا :

17 . f(x) = 2x -5 , h(x) = 5x +2

$$\begin{gathered} ( f\circ h)\left(x\right) = f( 5x +2) = 2( 5x+2) -5 = 10x +4 -5\mathbf{=}\mathbf{ }\mathbf{10}\mathit{x}\mathbf{ }\mathbf{-}\mathbf{1} \\ ( h\circ f)\left(x\right) = h( 2x -5) = 5( 2x -5) +2 = 10x -23 \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{للآخر}\mathbf{ }\mathbf{عكسيًا}\mathbf{ }\mathbf{ليس}\mathbf{ } \end{gathered}$$

$18. f\left(x\right) =\frac{2x}{3x +5} , h\left(x\right) = \frac{5x}{2 -3x }$

$$\begin{gathered} (f\circ h )\left(x\right) = f\left(\frac{5x }{2 -3x}\right) = \frac{2 \left(\frac{5x}{2-3x}\right)}{3 \left(\frac{5x}{2-3x}\right) +5 } = \frac{10x}{\frac{( 2-3x)( 15x+5(2-3x)}{(2 -3x)}} = \frac{10x }{15x +10 -15x }= \frac{10x}{10}= x \\ (h\circ f)\left(x\right) = h\left(\frac{2x}{3x +5 }\right) = \frac{5 \left(\frac{2x}{3x +5}\right)}{2 - 3 ( \frac{2x}{3x +5})}= \frac{\frac{10x}{3x +5}}{2- \frac{6x }{3x +5 }}= \frac{10x }{\frac{( 3x +5) ( 6x +10 -6x)}{(3x+5)}}= \frac{10x }{10}= x \\ \mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{للآخر}\mathbf{ }\mathbf{عكسيًا}\mathbf{ }\mathbf{منهما}\mathbf{ }\mathbf{كل}\mathbf{ }\mathbf{إذا}\mathbf{ } \end{gathered}$$

---

 

19. أمثل الاقتران العكسي للاقتران $f\left(x\right)=\sqrt[]{6+3x}$، ثم أمثل f(x) و f^-1 (x)  في المستوى الإحداثي نفسه .

$f\left(x\right)=\sqrt[]{6+3x}$

$\frac{y^{2 }- 6}{3}=x$

$f^{-1}\left(x\right)= \frac{x^{2 }-6}{3}$

 

 

---

 

20. هندسة : تعطى مساحة الدائرة بالاقتران $A\left(r\right)={\mathrm{\pi r}}^2$ حيث A المساحة ، و r نصف القطر. أعبر عن r  في صورة اقتران نسبة إلى المساحة A ، ثم أجد طول نصف قطر دائرة مساحتها  250cm²

^{$A={\mathrm{\pi r}}^2\Rightarrow \mathrm{r}=\sqrt[]{\frac{\mathrm{A}}{\mathrm{\pi }}}$}

 

^{$\mathrm{r}=\sqrt[]{\frac{250}{\mathrm{\pi } } }\mathbf{\simeq }\mathbf{ }\mathbf{8}\mathbf{.}\mathbf{92}$}

---

 

21 . فيزياء : يعطى زمن الدورة T ثانية لبندول بسيط بالاقتران $T\left(L\right)=2\mathrm{\pi }\sqrt[]{\frac{\mathrm{L}}{9.8}}$، حيث L طول البندول بالأمتار . أعبر عن L في صورة اقتران نسبة 

إلى الزمن T ، ثم أجد طول بندول زمن دورته 3s

$T\left(L\right)=2\mathrm{\pi }\sqrt[]{\frac{\mathrm{L}}{9.8}}$

 

${\left(\frac{\mathrm{T}}{2\mathrm{\pi }}\right)}^2(9.8)=\mathrm{L}$

 

${\left(\frac{3}{2\mathrm{\pi }}\right)}^2(9.8)=\mathrm{L}\Rightarrow \mathbf{L}\mathbf{=}\mathbf{2}\mathbf{.}\mathbf{23}$

---