الاقواس والقطاعات الدائرية

القوس هو جزء من الدائرة محدد بنقطتين عليها. والقطاع هو جزء من الدائرة محصور بين قوس منها ونصفي القطرين اللذين يمران بطر في القوس

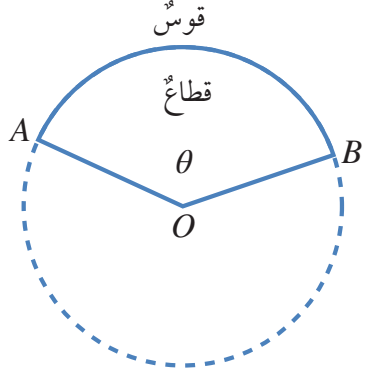
تمثل الزاوية AOB في الشكل المجاور زاوية القطاع الذي يعد كسرا من الدائرة. ويمكن استعمال قياس زاوية القطاع لكتابة هذا الكسر،  وذلك بقسمة قياس الزاوية على الدورة الكاملة؛ أي: $\frac{\theta }{360°}$، حيث $\theta$ قياس زاوية القطاع 

مثال 

يمثل الشكل المجاور قطاعا دائريا. أجد: 

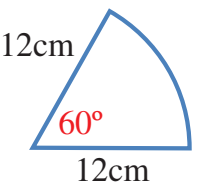
1) طول القوس (اكتب الإجابة بدلالة $\mathrm{\pi }$)

القطاع كسر من الدائرة، وهذا الكسر هو $\frac{60°}{360°}=\frac{1}{6}$. وبما أن طول قطر الدائرة $24cm$، فإن طول محيطها: $24\times \mathrm{\pi }=24\mathrm{\pi cm}$

إذا طول القوس يساوي $\frac{1}{6}$طول محيط الدائرة؛ أي: 

$24\mathrm{\pi }÷6=4\mathrm{\pi cm}$ 

                                                               

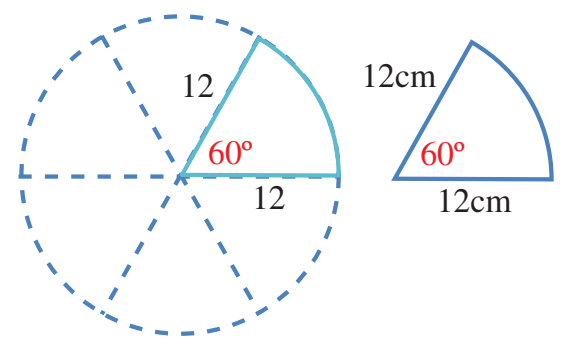
2) مساحة القطاع 

مساحة الدائرة هي: $\mathrm{\pi }\times {12}^2=144{\mathrm{\pi cm}}^2$

مساحة القطاع تساوي $\frac{1}{6}$ مساحة الدائرة؛ أي: $144\mathrm{\pi }÷6=24{\mathrm{\pi cm}}^2$

تعرفنا في المثال السابق أن القطاع هو كسر من الدائرة، وأنه يمكن دائما استعمال قياس زاوية القطاع لحساب طول القوس ومساحة القطاع الدائري 

مفهوم أساسي 

إذا كان قياس زاوية القطاع $\theta °$، وطول نصف قطر الدائرة r، وطول القوس l، ومساحة القطاع A، فإن: 

$$\begin{gathered} l=\frac{\theta }{360°}\times 2\mathrm{\pi r} \\ \mathrm{A}=\frac{\mathrm{\theta }}{360°}\times {\mathrm{\pi r}}^2 \end{gathered}$$

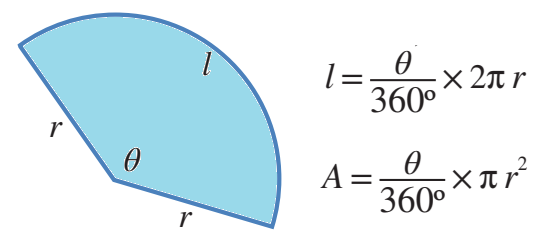
مثال 

أجد طول القوس ومساحة القطاع في الشكل المجاور

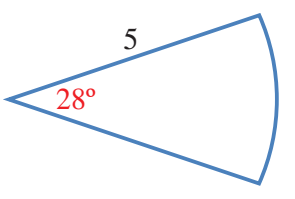
زاوية القطاع هي $28°$، وطول نصف القطر هو 5 وحدات طول: 

$$\begin{gathered} l=\frac{\theta }{360°}\times 2\mathrm{\pi r} \\ \mathrm{l}=\frac{28°}{360°}\times \mathrm{\pi }\times 2\times 5 \\ \approx 2.4 \end{gathered}$$

إذا، طول هذا القوس مقربا إلى أقرب منزلة عشرية واحدة هو: 2.4 وحدة طول 

$$\begin{gathered} A=\frac{\theta }{360°}\times {\mathrm{\pi r}}^2 \\ =\frac{28°}{360°}\times \mathrm{\pi }\times 5^2 \\ \approx 6.1 \end{gathered}$$

إذا مساحة هذا القطاع مقربة إلى أقرب منزلة عشوية واحدة هي: 6.1 وحدة مربعة 

مفهوم أساسي 

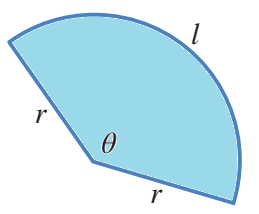
محيط القطاع الدائري (L) هو المسافة حول القطاع، وهي تساوي طول قوس القطاع، مضافا إليه مثلا طول نصف قطر الدائرة:

$L=\frac{\theta }{360°}\times 2\mathrm{\pi r}+2\mathrm{r}$

مثال 

أجد محيط القطاع الدائرة في الشكل المجاور، مقربا إجابتي إلى أقرب منزلة عشرية واحدة 

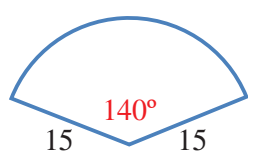
زاوية القطاع هي $140°$، وطول نصف القطر هو 15 وحدة طول: 

$$\begin{gathered} L=\frac{\theta }{360°}\times 2\mathrm{\pi r}\times 2\mathrm{r} \\ =\left(\frac{140°}{360°}\times 2\times \mathrm{\pi }\times 15\right)+2\times 15 \\ \approx 66.6519 \end{gathered}$$

إذا،  محيط هذا القطاع مقربا إلى أقرب منزلة عشرية واحدة هو:66.7 وحدة طول 

مثال: من الحياة 

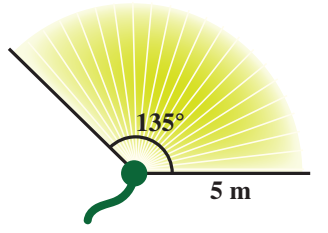
حديقة منزل وضع في أحد أطرافها مرش للماء، يدور حول الرأس بزاوية مقدارها $135°$، فيصل الماء إلى مسافة 5m من المرش. أجد مساحة المنطقة التي سيرويها هذا المرش، مقربا إجابتي أقرب منزلة عشرية واحدة 

تمثل المنطقة التي سيرويها المرش قطاعا دائريا زاويته $135°$، وطول نصف قطره 5m: 

$$\begin{gathered} A=\frac{\theta }{360°}\times {\mathrm{\pi r}}^2 \\ =\frac{135°}{360°}\times \mathrm{\pi }\times 5^2 \\ \approx 29.5 \end{gathered}$$

إذا، مساحة المنطقة مقربة إلى أقرب منزلة عشرية واحدة هي: $29.5m^2$