رياضيات فصل أول

التحويلاتُ الهندسيَّةُ للاقترانِ التربيعيِّ

أولًا : الانسحابُ

الانسحاب الرأسي 

عند إضافة الثابت الموجب K  إلى قاعدة الاقتران الرئيس f(x) أو طرحه منها فإن مُنحنى الاقتران $f\left(x\right) \pm k$ هُو مُنحنى الاقتران الرئيس مُزاحًا إلى

الأعلى أو إلى الأسفل بمقدار K  وحدةً، ويُسمى هذا التحويلُ الانسحاب الرأسي.

مفهومٌ أساسيٌّ (الانسحابُ الرأسيُّ للاقترانِ التربيعيِّ)

إذا كان $f\left(x\right) = x^2$ وكان k عددًا حقيقيًّا موجبًا، فإنَّ: 

• مُنحنى $g\left(x\right) = x^2 + k$ مُزاحًا إلى الأعلى k وحدة.

• مُنحنى $g\left(x\right) = x^2 - k$ مُزاحًا إلى الأسفل k وحدة.

 

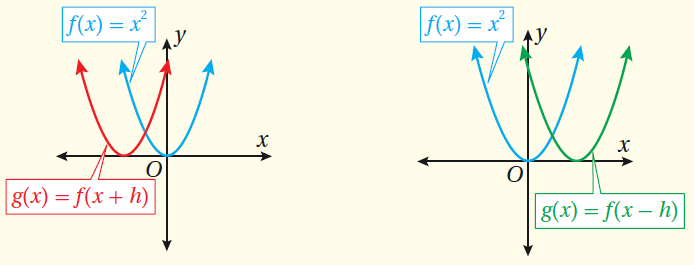
الانسحابَ الأفقيَّ 

عند إضافة الثابت الموجب h إلى قيم x جميعها في مجال الاقتران f(x) أو طرحه منها، فإن مُنحنى الاقتران $f(x \pm h)$ هُو مُنحنى الاقتران الرئيس

مُزاحًا إلى اليمين أو إلى اليسار بمقدار h وحدةً، ويُسمى هذا التحويلُ الانسحاب الأفقي.

مفهومٌ أساسيٌّ (الانسحابُ الأفقيُّ للاقترانِ التربيعيِّ)

إذا كان $f\left(x\right) = x^2$ وكان h عددًا حقيقيًّا موجبًا، فإنَّ : 

•  مُنحنى $g\left(x\right) = {(x-h)}^2$ هو منحنى f(x) مُزاحًا إلى اليمينِ h وحدةً.

• مُنحنى $g\left(x\right) = {(x+h)}^2$ هو منحنى f(x) مُزاحًا إلى اليسار h وحدةً.

 

 

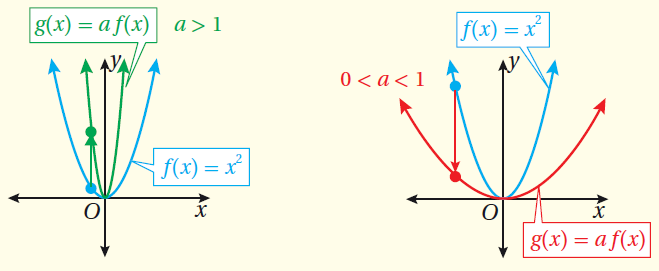
ثانيًا : التمدُّدُ

التمدُّدُ : هُوَ تحويلٌ هندسيٌّ يؤدّي إلى توسيعِ مُنحنى الاقترانِ أوْ تضييقِهِ، فعندَ ضربِ الاقترانِ الرئيسِ (f(x بالثابتِ a ؛ حيثُ a عددٌ حقيقيٌّ موجِبٌ،

فإنَّ مُنحنى الاقترانِ a f(x) هُوَ توسيعٌ أوْ تضييقٌ رأسيٌّ لِمُنحنى الاقترانِ f(x).  

مفهومٌ أساسيٌّ (تمددُ الاقترانِ التربيعيِّ)

إذا كان $f\left(x\right) =x^2$ وكان a عددًا حقيقيًّا موجبًا، فإنَّ مُنحنى $g\left(x\right) = a{x}^2$ هو :

• توسيع رأسي بمعاملٍ مقدارُهُ a لِمُنحنى (f(x ، إذا كانتْ  a > 1  

• تضييق رأسي بمعاملٍ مقدارُهُ a لِمُنحنى (f(x  ، إذا كانتْ $0 < a < 1$

 

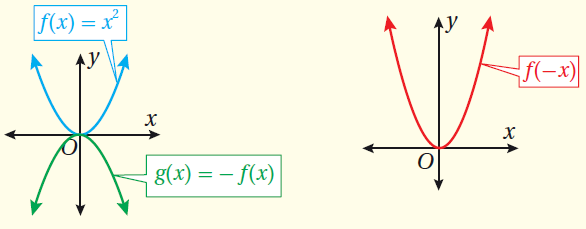
ثالثًا : الانعكاسُ

الانعكاسُ : هُوَ تحويلٌ هندسيٌّ يعكِسُ مُنحنى الاقترانِ حولَ مُستقيمٍ مُحَدَّدٍ.

مفهومٌ أساسيٌّ (الانعكاسُ)

إذا كان $f\left(x\right) =x^2$ ، فإنَّ : 

•  مُنحنى (g(x) = -f(x ، هُوَ انعكاسٌ لِمُنحنى (f(x حولَ المحورِ x

•  مُنحنى (g(x) = f(-x ، هُوَ انعكاسٌ لِمُنحنى ( f(x حولَ المحورِ y