رياضيات فصل أول

نتاجات الدرس: رسم منحنيات اقترانات ، باستعمال التحويلات الهندسية ، وكتابة معادلة التحويل لمنحنى معطى .

• الاقترانات الرئيسة: 
عائلة الاقترانات وهي مجموعة الاقترانات التي تشابه منحنياتها في صفة واحدة أو أكثر ، ويسمى أبسط اقترانات هذه العائلة الاقتران الرئيس فمثلاً ، الاقتران الرئيس لعائلة الاقترانات الخطية هو :  f(x)=x ، وفي ما يأتي الاقترانات الرئيسة الأكثر شيوعاً: 
 

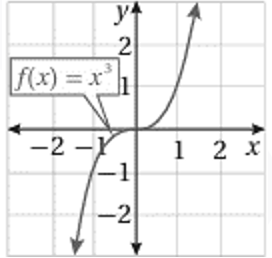
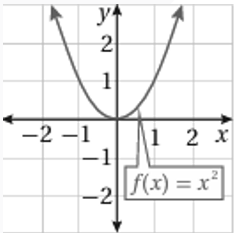
2) الاقتران التكعيبي الرئيس $f\left(x\right)=x^3$	1) الاقتران التربيعي الرئيس $f\left(x\right)=x^2$
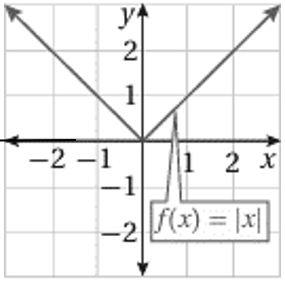
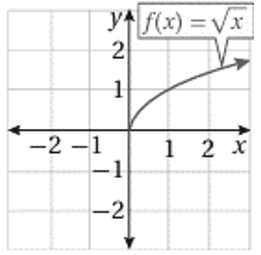
4) اقتران القيمة المطلقة الرئيس $f\left(x\right)=\left|x\right|$	3) اقتران الجذر التربيعي الرئيس $f\left(x\right)=\sqrt{x}$

- إن معرفة شكل منحنى الاقتران الرئيس يساعد على تحليل وتمثيل منحنيات الاقترانات الأكثر تعقيداً ، الناتجة عن تطبيق تحويل هندسي او أكثر على منحنى الاقتران الرئيس.

- بعض هذه التحويلات يغير موقع المنحنى فقط ولا يغير في شكله وأبعاده.  مثل: تحويلات الانعكاس والانسحاب. - والبعض الآخر يغير شكل المنحنى بحيث تبدو أوسع او أضيق من منحنى الاقتران الرئيس. مثل: تحويلات التمدد.

---

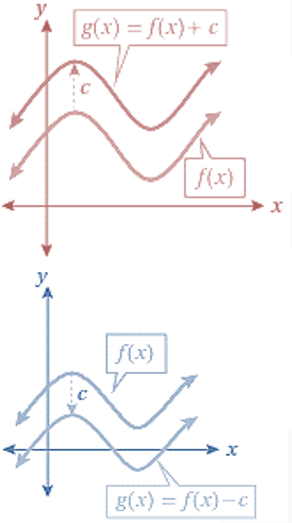
أولاً : الانسحاب الرأسي: وهو تحويل هندسي ينقل منحنى الاقتران الى الأعلى عند إضافة ثابت موجب الى الاقتران ، والى الأسفل عند طرح ثابت موجب من الاقتران .   اذا كان f اقتراناً وكان c عدداً حقيقياً موجباً ، فإن :  منحنى $g\left(x\right)=f\left(x\right)+c$ هو منحنى f(x) مزاحاً إلى الأعلى c وحدة . منحنى $g\left(x\right)=f\left(x\right)-c$ هو منحنى f(x) مزاحاً إلى الأسفل c وحدة .

مثال (1): أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$ لتمثيل كل من الاقترانات الآتية بيانياً : 

1) $g\left(x\right)=x^2+3$                                     2) $g\left(x\right)=x^2-4$

الإجابة:

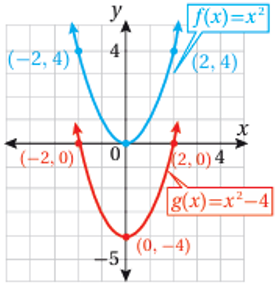
1) منحنى $g\left(x\right)=x^2+3$ هو منحنى $f\left(x\right)=x^2$ مزاحاً 3 وحدات الى الأعلى على المحور y .

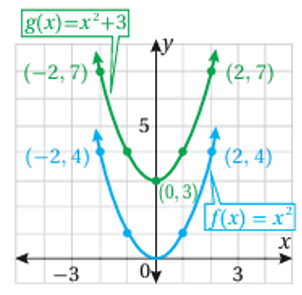
2) منحنى $g\left(x\right)=x^2-4$ هو منحنى $f\left(x\right)=x^2$  مزاحاً 4 وحدات الى الأسفل على المحور y.

---

تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=\left|x\right|$ ، لتمثيل الاقتران الآتي بيانياً: $g\left(x\right)=\left|x\right|+3$

---

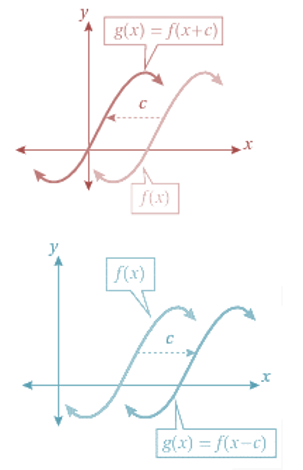
ثانياً: الانسحاب الأفقي: وهو تحويل هندسي ينقل منحنى الاقتران الى اليسار عند إضافة ثابت موجب الى قيم $x$ جميعها في مجال الاقتران ، والى اليمين عند طرح ثابت موجب من قيم $x$ جميعها في مجال الاقتران. اذا كان $f$ اقتراناً وكان $c$ عدداً حقيقياً موجباً، فإن:  منحنى $g\left(x\right)=f(x+c)$ هو منحنى $f\left(x\right)$ مزاحاً إلى اليسار $c$ وحدة . منحنى $g\left(x\right)=f(x-c)$ هو منحنى $f\left(x\right)$ مزاحاً إلى اليمين $c$ وحدة .

مثال (2): أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$ لتمثيل كل من الاقترانات الآتية بيانياً: 
1) $g\left(x\right)={(x-2)}^2$                         2) $g\left(x\right)={(x+4)}^2$

الإجابة:

1) منحنى $g\left(x\right)={(x-2)}^2$ هو منحنى $f\left(x\right)=x^2$ مزاحاً وحدتين الى اليمين ، على المحور $x$

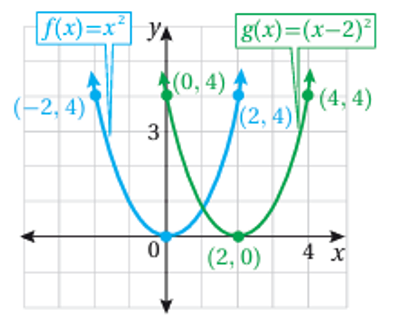
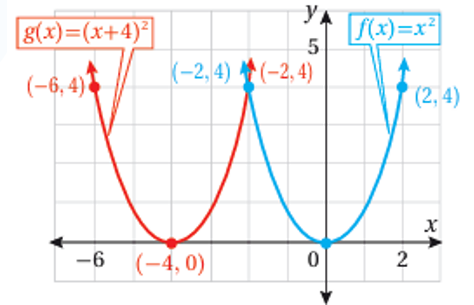
2) منحنى $g\left(x\right)={(x+4)}^2$ هو منحنى $f\left(x\right)=x^2$ مزاحاً 4 وحدات الى اليسار على المحور $x$

---

تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^3$ لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)={(x-2)}^3$              2) $g\left(x\right)={(x+2)}^3-4$

---

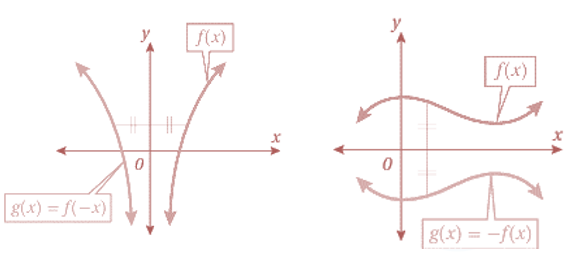
الانعكاس: وهو تحويل هندسي يعكس منحنى الاقتران حول مستقيم محدّد . منحنى $g\left(x\right)=-f\left(x\right)$ هو انعكاس لمنحنى f(x) حول المحور x . منحنى $g\left(x\right)=f(-x)$ هو انعكاس لمنحنى f(x) حول المحور y .

مثال (3): أستعمل منحنى الاقتران الرئيس  $f\left(x\right)=\sqrt{x}$ لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)=-\sqrt{x}$                     2) $g\left(x\right)=\sqrt{-x}$

الإجابة:

1) منحنى $g\left(x\right)=-\sqrt{x}$ هو انعكاس لمنحنى f(x) حول المحور  x ، أي أن كل نقطة $(x,y)$ على منحنى f تقابل النقطة $(x,-y)$ على منحنى g.

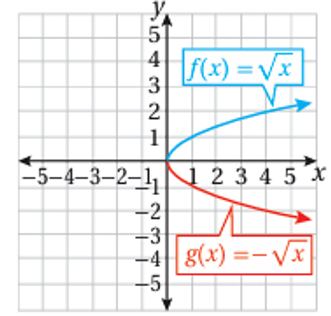
2) منحنى $g\left(x\right)=\sqrt{-x}$ هو انعكاس لمنحنى f(x) حول المحور Y، أي أن كل نقطة $(x,y)$ على منحنى f تقابل النقطة $(-x,y)$ على منحنى g.

---

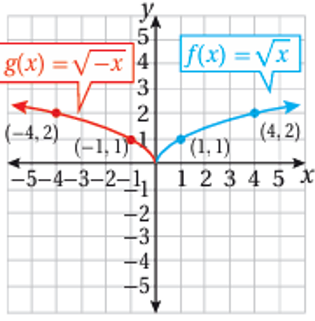
تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=\left|x\right|$ لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)=-\left|x\right|$                    2) $g\left(x\right)=|-x|$

 

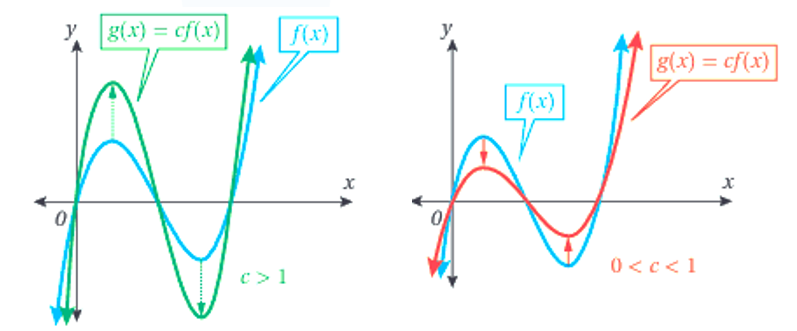
التمدد الرأسي: وهو تحويل هندسي يؤدي الى توسيع منحنى الاقتران او تضييقه رأسياً . اذا كان c عدداً حقيقياً موجباً ، فإن منحنى $g\left(x\right)=cf\left(x\right)$ هو :  توسيع رأسي بمعامل مقداره c لمنحنى f(x) ، اذا كانت $c>1$   تضييق رأسي بمعامل مقداره c لمنحنى f(x) ، اذا كانت $0<c<1$

مثال 4: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=\sqrt{x}$ لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)=2\sqrt{x}$                 2) $g\left(x\right)=\frac{1}{2}\sqrt{x}$

الإجابة:

1) منحنى $g\left(x\right)=2\sqrt{x}$ هو توسيع رأسي لمنحنى  $f\left(x\right)=\sqrt{x}$ بمعامل مقداره $2$

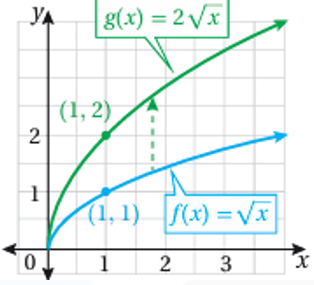
2) منحنى $g\left(x\right)=\frac{1}{2}\sqrt{x}$ هو تضيق رأسي لمنحنى $f\left(x\right)=\sqrt{x}$ بمعامل مقداره $\frac{1}{2}$

---

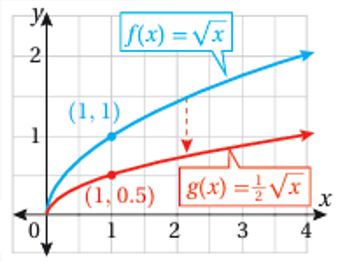
تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$  لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)=3x^2$                                           2) $g\left(x\right)=\frac{1}{3}{x}^2$

 

---

التمدد الأفقي: وهو تحويل هندسي يؤدي الى توسيع منحنى الاقتران أو تضييقه أفقياً . اذا كان c عدداً حقيقياً موجباً ، فإن منحنى $g\left(x\right)=f\left(cx\right)$ هو :  تضييق أفقي لمنحنى f(x) ، اذا كانت $c>1$ بمعامل مقداره $\frac{1}{c}$ توسيع أفقي لمنحنى f(x) ، اذا كانت 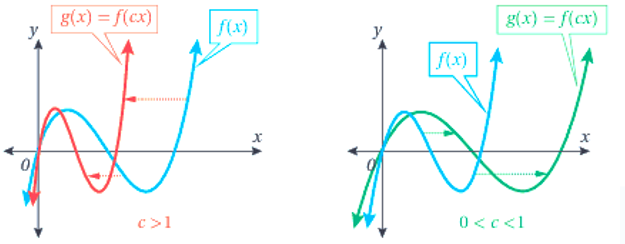$0<c<1$ بمعامل مقداره $\frac{1}{c}$

مثال (5): أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$  لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)={\left(2x\right)}^2$                          2) $g\left(x\right)={\left(\frac{1}{2}x\right)}^2$

الإجابة:

1) منحنى  $g\left(x\right)={\left(2x\right)}^2$ هو تضييق أفقي لمنحنى $f\left(x\right)=x^2$ بمعامل مقداره $\frac{1}{2}$

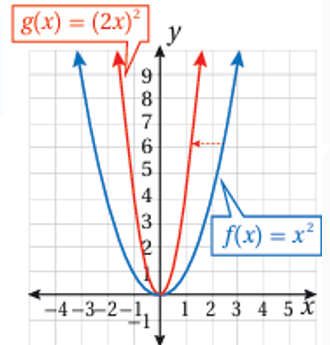
2) منحنى $g\left(x\right)={\left(\frac{1}{2}x\right)}^2$ هو توسيع أفقي لمنحنى $f\left(x\right)=x^2$ بمعامل مقداره 2

---

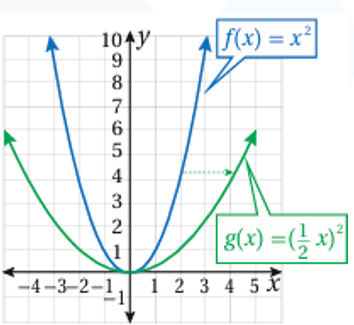
تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$ لتمثيل كل من الاقترانات الآتية بيانياً: 

1) $g\left(x\right)={\left(4x\right)}^2$                         2) $g\left(x\right)={\left(\frac{1}{4}x\right)}^2$

---

• سلسلة التحويلات الهندسية:  يمكن تمثيل منحنى اقتران ناتج عن تطبيق اكثر من تحويل هندسي على الاقتران الرئيس بتطبيق التحويلات على الاقتران الرئيس بالترتيب الآتي :  أولاً: الانعكاس  $\mathbf{\leftarrow }$ ثانيا: التمدد $\mathbf{\leftarrow }$  ثالثا: الانسحاب

مثال (6) : أستعمل منحنى الاقتران الرئيس $f\left(x\right)=\sqrt{x}$ لتمثيل منحنى $g\left(x\right)=\sqrt{1-x}+2$ بيانيا.

الإجابة:

بما أن الانسحاب الأفقي الى اليمين يكتب على صورة $x-c$ ، ابدأ بإعادة كتابة الاقتران g على الصورة الآتية : 
أولا: نمثل منحنى $f\left(x\right)=\sqrt{x}$

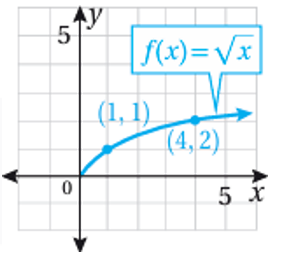
ثانياً: نمثل منحنى $y=\sqrt{-x}$ بإجراء انعكاس لمنحنى f(x) حول المحور y 

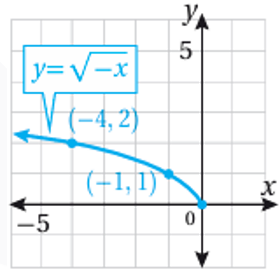
ثالثاً: نمثل منحنى  $y=\sqrt{-(x-1)}$ بإجراء انسحاب لمنحنى $y=\sqrt{-x}$ وحدة واحدة الى اليمين .

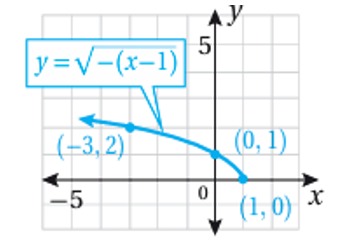
رابعاً: نمثل منحنى $y=\sqrt{-(x-1)}+2$ بإجراء انسحاب للمنحنى وحدتان الى الأعلى 

---

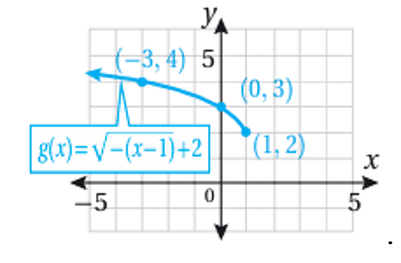
تدريب: أستعمل منحنى الاقتران الرئيس $f\left(x\right)=x^2$  لتمثيل منحنى $g\left(x\right)=-(x-2{)}^2+3$ بيانياً: