حلول أسئلة التحويلات الهندسية للاقترانات
أتحقق من فهمي صفحة 22
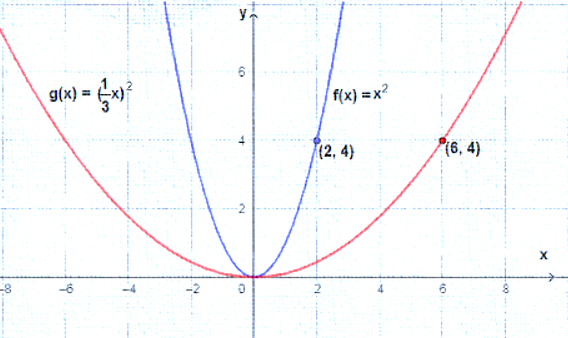
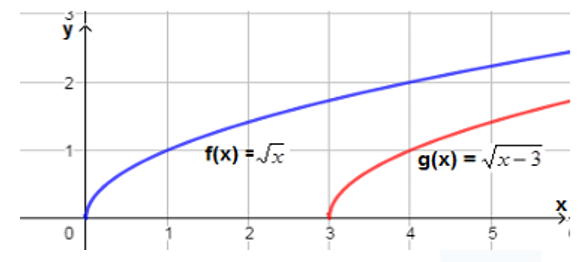
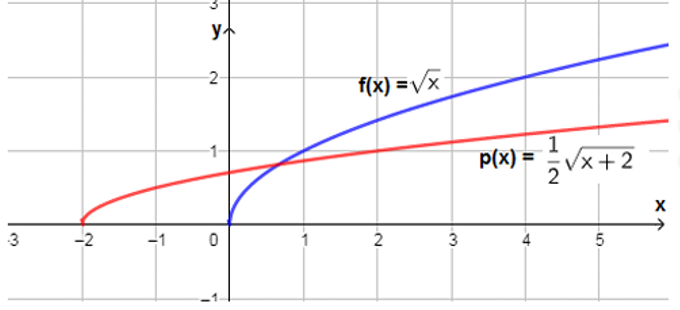
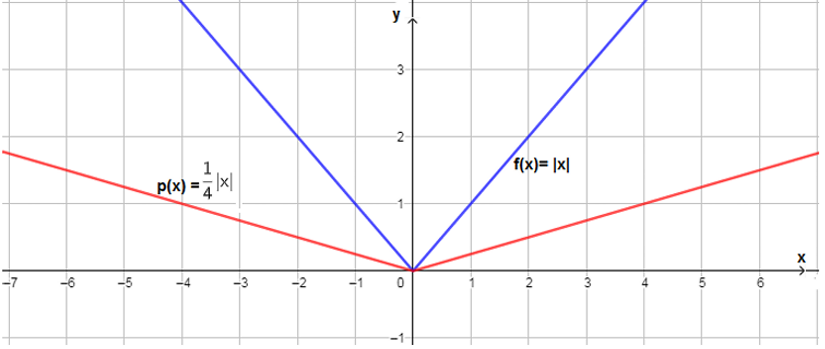
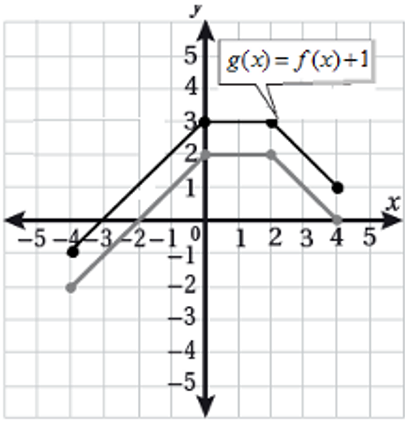
أستعملُ منحنى الاقتران الرئيس ، لتمثيل كلّ من الاقترانات الآتية بيانيًّا:
| a) |
| b) |
الحل:
|
a)
|
b)
|
أتحقق من فهمي صفحة 23
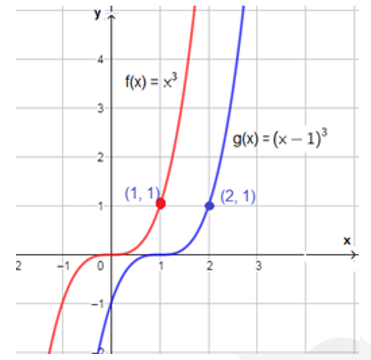
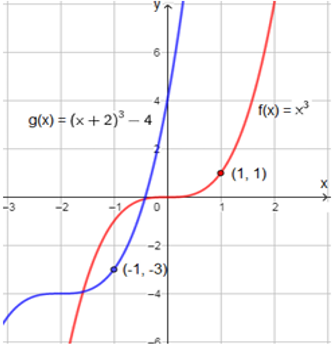
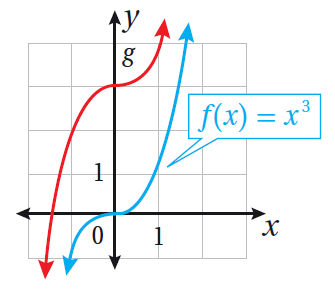
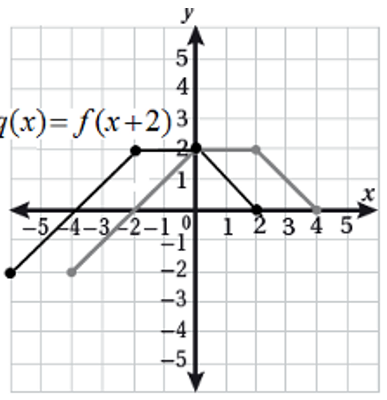
أستعملُ منحنى الاقتران الرئيس f(x) = x3 ، لتمثيل كلّ من الاقترانات الآتية بيانيًّا:
| c) g(x) = (x + 2)3 - 4 | b) g(x) = (x+1)3 | a) g(x) = (x-1)3 |
الحل:
|
a)
|
b)
|
c)
|
أتحقق من فهمي صفحة 25
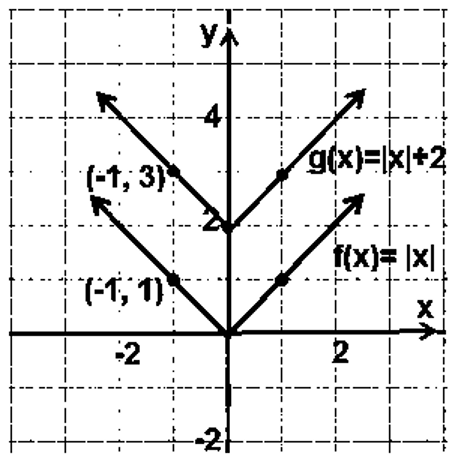
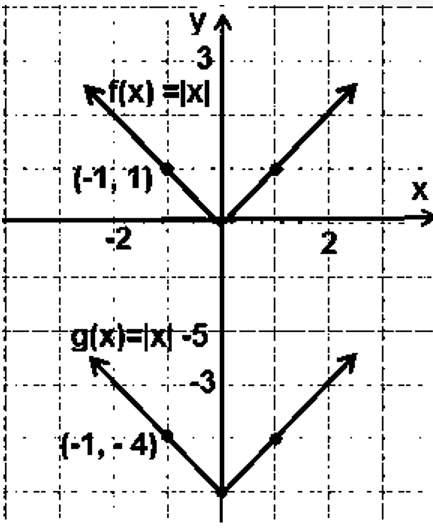
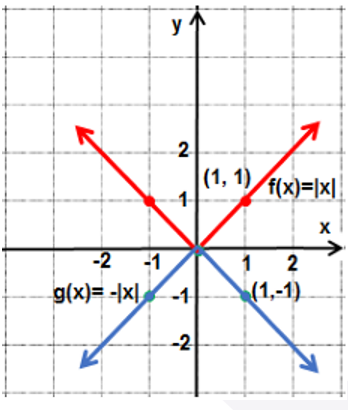
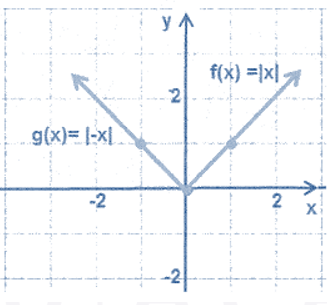
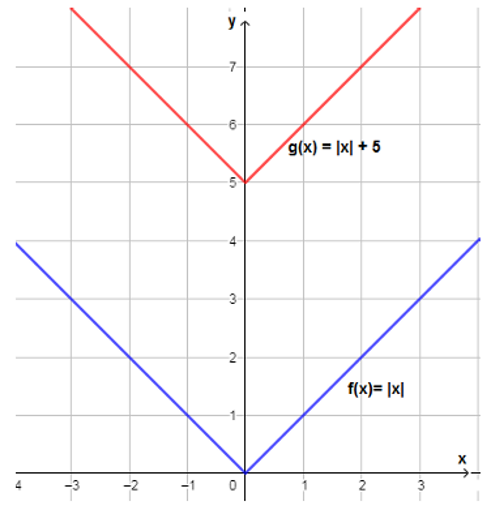
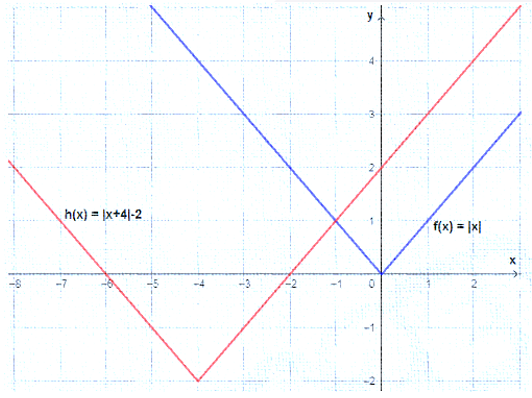
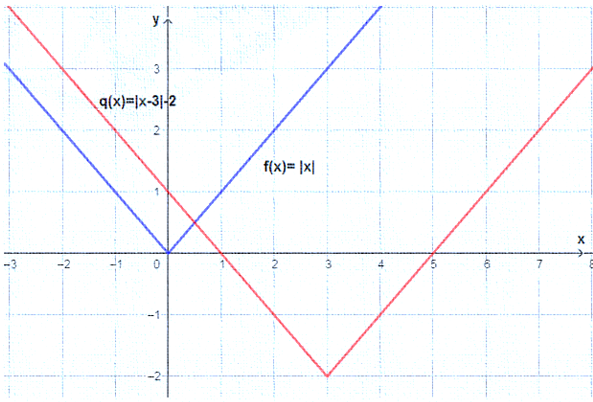
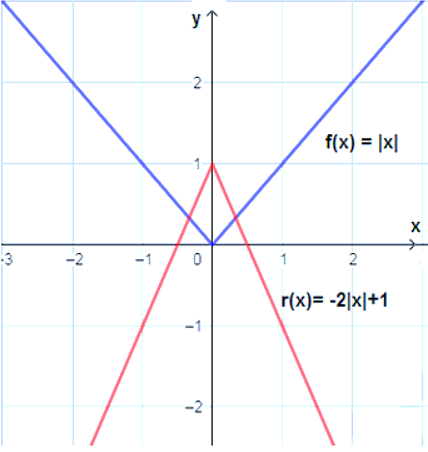
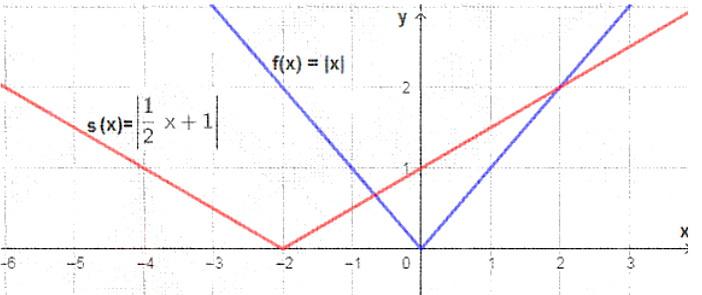
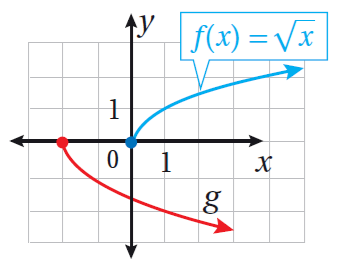
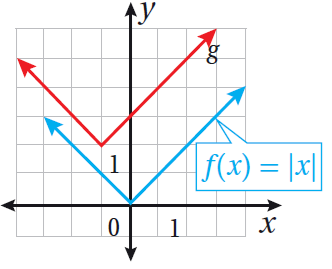
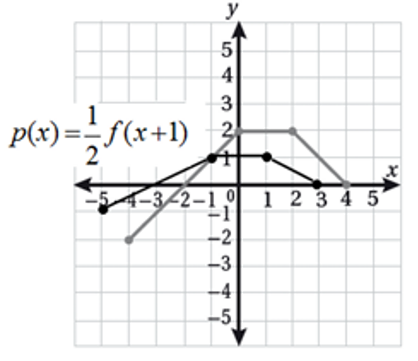
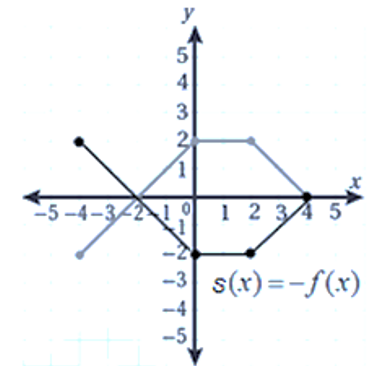
أستعملُ منحنى الاقتران |f(x) = |x لتمثيل كلّ الاقترانات الآتية بيانيًّا:
| b) g(x) = |-x| | a) g(x) = -|x| |
الحل:
|
a)
|
b) يتطابق منحنى مع منحنى لأنه متماثل حول المحور y ، فبالانعكاس حول المحور y يبقى المنحنى على وضعه دون تغيير .
|
أتحقق من فهمي صفحة 27
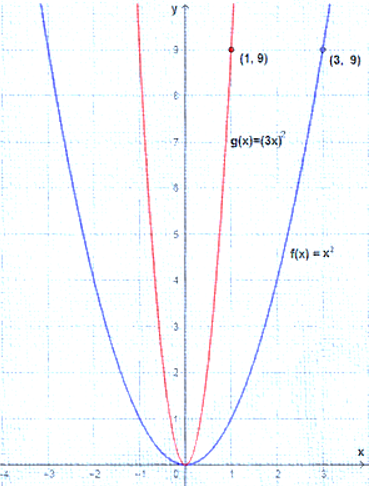
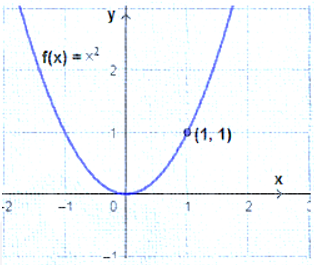
أستعملُ منحنى الاقتران الرئيس f(x) = x2 لتمثيل كلّ من الاقترانات الآتية بيانيًّا:
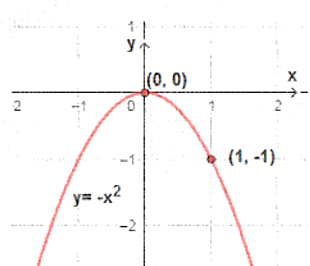
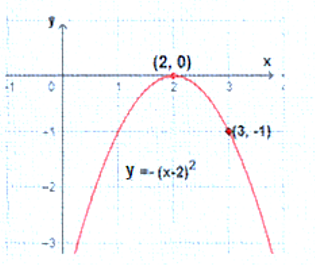
| a) | b) |
الحل:
|
a)
|
b)
|
أتحقق من فهمي صفحة 28
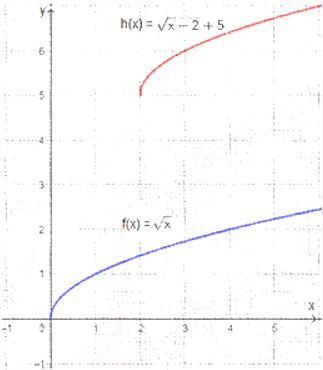
أستعملُ منحنى الاقتران الرئيس لتمثيل منحنى بيانيًّا.
الحل:
|
أولًا: رسم
|
ثانيًا: رسم انعكاس حول المحور
|
|
ثالثًا: انسحاب وحدتين إلى اليمين
|
رابعًا: انسحاب 3 وحدات إلى الأعلى
|
أتدرّب وأحلّ المسائل صفحة 29
أستعملُ منحنى الاقتران الرئيس f(x) = x2 لتمثيل منحنى كلّ من الاقترانات الآتية بيانيًّا:
| 1) | 2) | 3) |
الحل:
|
1)
|
2)
|
3)
|
أستعملُ منحنى الاقتران الرئيس لتمثيل منحنى كلّ من الاقترانات الآتية بيانيًّا:
| 4) | 5) | 6) |
الحل:
|
4)
|
5)
|
6)
|
أستعملُ منحنى الاقتران الرئيس |f(x) = |x ، لتمثيل منحنى كلّ من الاقترانات الآتية بيانيًّا:
| 7) | 8) | 9) |
| 10) | 11) | 12) |
الحل:
|
7)
|
8)
|
9)
|
|
10)
|
11)
|
|
|
12)
|
||
إذا كان منحنى الاقتران g ناتج عن تحويل هندسي أو أكثر لمنحنى الاقتران f؛ فأجد قاعدة الاقتران g في كلّ ممّا يأتي:
|
15)
|
14)
|
13)
|
الحل:
| 13) | 14) | 15) |
16) يُبيّن التمثيل البياني المجاور منحنى الاقتران f(x) (باللون الأزرق). أُحدّد رقم منحنى كلّ اقتران ممّا يأتي:
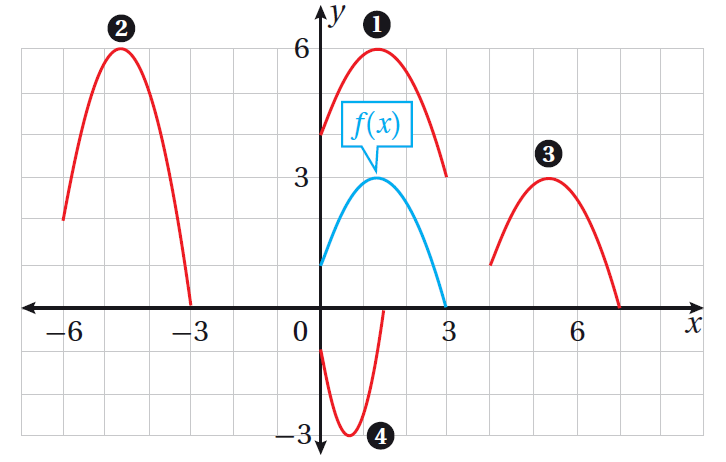
| a) g(x)=f(x-4) | b) h(x)=f(x)+3 |
| c) g(x)=2f(x+6) | d) h(x)=-f(2x) |
الحل:
|
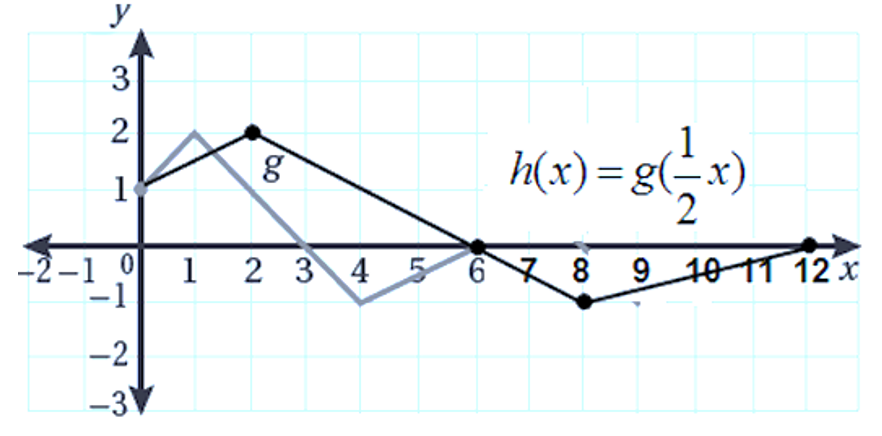
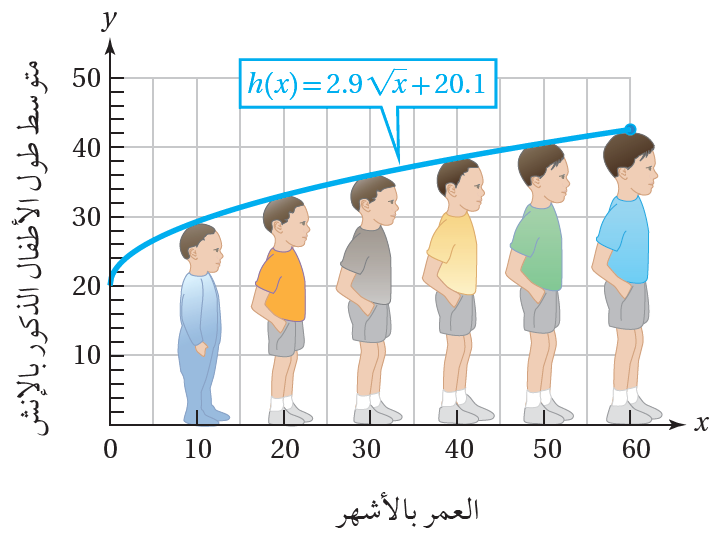
يُمثّل الاقتران متوسّط طول الأطفال الذكور بالإنش، حيث x العمر بالأشهر. 17) أصف التحويلات التي طُبّقت على الاقتران الرئيس للحصول على (h(x. |
 |
الحل:
17) تمدد (توسيع) رأسي معامله 2.9 ، وانسحاب الى الأعلى بمقدار 20.1 وحدة .
18) متوسط الطول للاطفال بعمر 5 سنوات هو:
19) الثابت 20.1 يمثل متوسط اطوال الاطفال الذكور عند الولادة .
20) أحلّ المسألة الواردة في بند (مسألة اليوم).
الحل:
منحنى ناتج عن تضييق رأسي معامله لمنحنى متبوعاً بانسحاب بمقدار وحدة واحدة الى الاعلى .
مهارات التفكير العليا
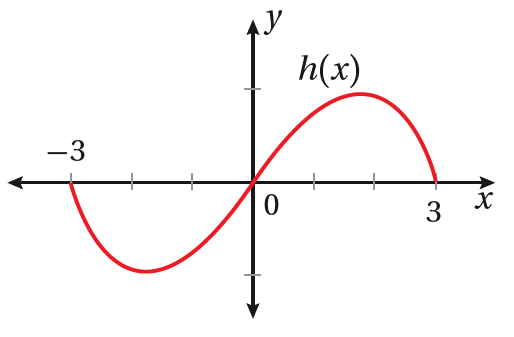 |
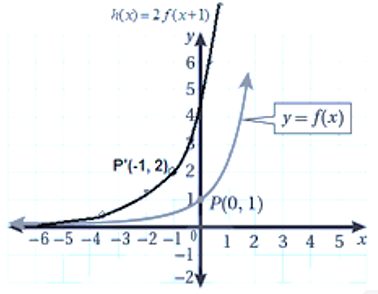
تبرير: أستعملُ التمثيل البياني المجاور الذي يُبيّن منحنى (h(x ؛ لتمثيل منحنى كلّ من الاقترانات الآتية بيانيًّا، وأبرّر إجابتي: 21) 22) |
|
الحل:
21) ضرب الاحداثي x لكل نقطة في
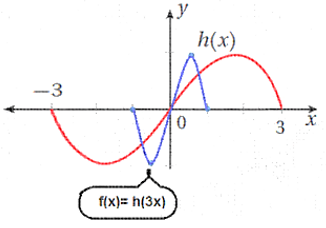
22) ضرب الاحداثي x لكل نقطة في 3
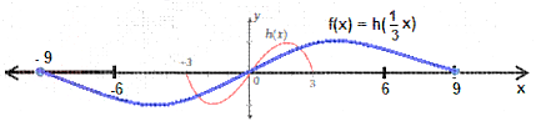
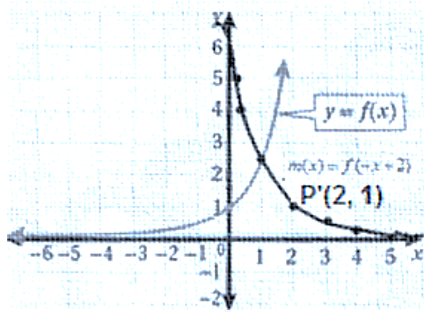
تبرير: أفترضُ أنّ نقطة على منحنى الاقتران . أُحدّد النقطة المقابلة لها على منحنى كلّ اقتران ممّا يأتي، وأبرّر إجابتي:
| 23) | 24) | 25) |
الحل:
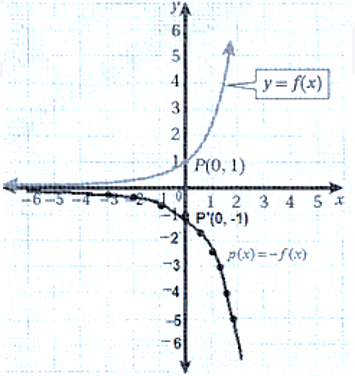
23) لأن منحنى هو انعكاس لمنحنى حول المحور Y.
24) لأن منحنى هو توسيع لمنحنى معامله 2 ، لذلك يضرب الاحداثي y في 2.
25) لأن منحنى هو انعكاس حول المحور y لمنحنى ثم انسحاب إلى اليمين بمقدار 3 وحدات.
26) تحدّ: في الشكل المجاور إذا كان منحنى الاقتران ناتج عن تحويل هندسي أو أكثر لمنحنى الاقتران ؛ فأجد قاعدة الاقتران .
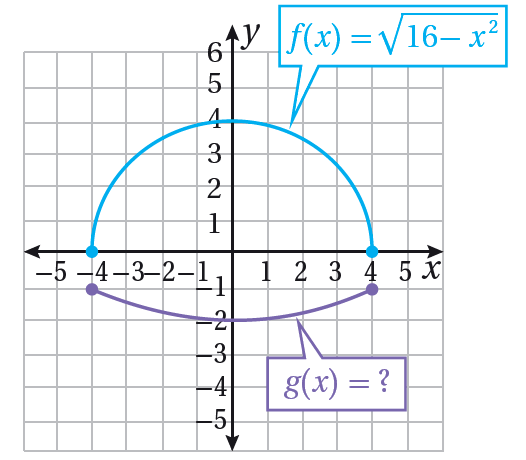
الحل:
منحنى ناتج عن انعكاس حول المحور وتضييق رأسي وانسحاب بمقدار وحدة للأسفل .
فتكون قاعدته: وبتعويض احداثيي النقطة .
كتاب التمارين
|
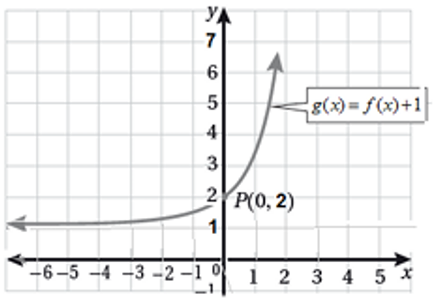
أستعملُ التمثيل البياني المجاور الذي يُبيّن منحنى ( f(x ؛ لتمثيل منحنى كُلّ من الاقترانات الآتية، وأبيّن إحداثيَي النقطة P في كل حالة:
|
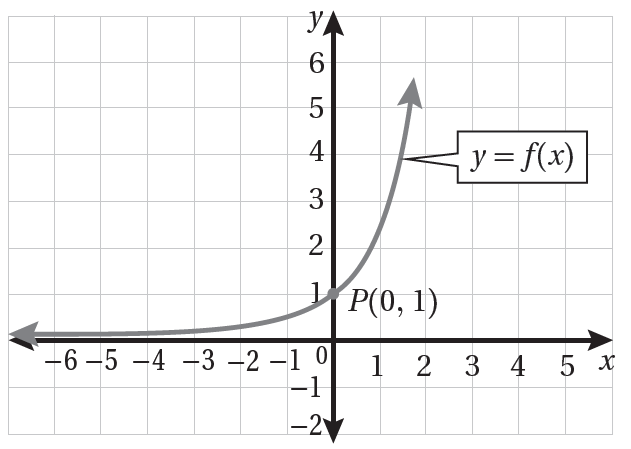 |
الحل:
|
1)
|
2)
|
|
3)
|
4)
|
أصف التحويلات التي تمّت على (f(x للحصول على (g(x في كُلّ ممّا يأتي:
5) 6)
الحل:
5) انعكاس حول المحور x ، وتوسيع رأسي معامله 3 ، وانسحاب الى اليمين بمقدار وحدتين ، واخيراً انسحاب الى الأعلى بمقدار 5 وحدات .
6) انعكاس حول المحور y ، وتوسيع رأسي معامله 2 ، وانسحاب الى اليمين بمقدار 4 وحدات ، واخيراً انسحاب الى الأسفل بمقدار 3 وحدات .
|
أستعملُ التمثيل البياني المجاور الذي يُبيّن منحنى (f(x ؛ لتمثيل منحنى كُلّ من الاقترانات الآتية:
|
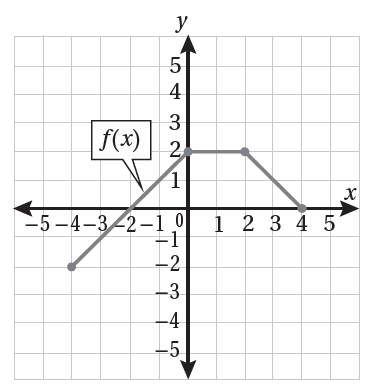 |
الحل:
|
7)
|
8)
|
|
9)
|
10)
|
11) سكّان: يُمثّل الاقتران عدد سكّان أحد التجمّعات السكنية؛ إذ يُمثّل t عدد السنوات منذ تأسيس هذا التجمّع في عام 1985 م.
أصف التحويلات التي تمّت على الاقتران للحصول على الاقتران .
الحل:
تضييق رأسي معامله 0.1 ، وانسحاب الى الاعلى بمقدار 3000 وحدة .
|
أستعملُ التمثيل البياني المجاور الذي يُبيّن منحنى (g(x ؛ لتمثيل منحنى كُلّ من الاقترانات الآتية: |
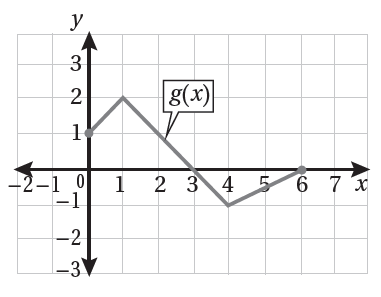 |
الحل:
12)

13)