رياضيات أدبي فصل ثاني

التزايد والتناقص لكثيرات الحدود

Increasing and Decreasing of Polynomials

فكرة الدرس : تحديد النقاط الحرجة ، وفترات التزايد والتناقص لكثيرات الحدود حتى الدرجة الثالثة.

أولًا  : النقاط الحرجة

توجد على منحنى اقتران كثير الحدود  f المبين جانبًا نقطة واحدة على الأقل يُمكن رسم مماس أفقي

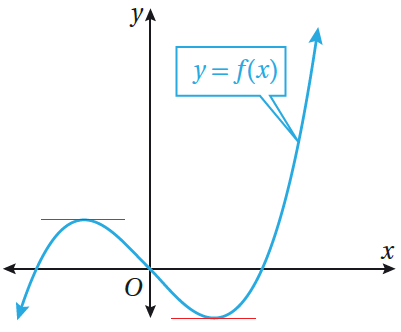عندها في ما يعرف بالنقطة الحرجة ، وهذا يعني أنّ مشتقة الاقتران عند هذه النقطة تساوي صفرًا ،

وأنه توجد قيمة حرجة للاقتران عند الإحداثي x  للنقطة الحرجة.

إيجاد النقاط الحرجة لكثيرات الحدود (جبريًا) :  

مثال : 

أجد النقاط الحرجة للاقتران : f(x)=3x²+ 12x

الحل : 

1) اشتقاق الاقتران	$f\text{'}\left(x\right) = 6x +12$
2)  المشتقة = صفر	$6x +12 = 0$
3) حل المعادلة الناتجة لإيجاد قيمة x	$6x+12 = 0$ $6x +12 -12 = 0 -12$ $$\begin{gathered} \mathrm{} \\ 6x = -12 \end{gathered}$$ $x = -2$

 

 

 

 

 

 

 

 

 

 

إذن عند x  = - 2  قيمة حرجة للاقتران f(x) ، قيمتها :

$f(-2)= 3{(-2)}^2 +12(-2)= -12$  

وعليه فالنقطة الحرجة على منحنى الاقتران f(x)  ، هي : $(-2 , f(-2\left)\right)$ ، أي : $(-2,-12)$

 

الرسم المجاور يوضح موقع النقطة الحرجة للاقتران f ، والتي منها يُمكن رسم مماس أفقي (يوازي محور x).

 

 

 

 

 

 

 

 

 

ثانيًا : تزايد الاقتران وتناقصه  

يبين الشكل المجاور التمثيل البياني لاقتران كثير الحدود $y = f\left(x\right)$   ، ألاحظ أن قيم y  تزداد في الفترة  $-\infty < x < a$  والفترة $b< x <\infty$ وأنّ منحنى الاقتران يرتفع من اليسار إلى اليمين في هاتين الفترتين ؛ لذا يكون الاقتران f متزايدًا فيهما .  ألاحظ أيضًا أنّ قيم y تقل في الفترة $a < x < b$  ، وأن منحنى الاقتران ينخفض من اليسار إلى اليمين ؛ لذا يكون الاقتران f  متناقصًا في هذه الفترة .

 

 

 

 

 

 

 

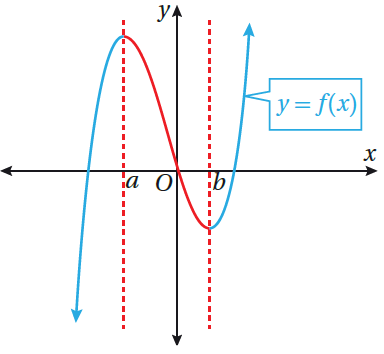 مفهوم أساسي (تزايد الاقتران وتناقصه)

• يكون الاقتران f متناقصًا في الفترة المفتوحة I  ، إذا كان لكل $x_{1 }< x_2$  في الفترة $f\left(x_1\right) > f\left(x_2\right)$

• يكون الاقتران f متزايدًا في الفترة المفتوحة I  ، إذا كان لكل $x_1< x_2$ في الفترة $f\left(x_1\right) < f\left(x_2\right)$
 

                                             

---

تعلّمتُ سابقًا أنّ مشتقة الاقتران عند نقطة ما تساوي ميل المماس عند هذه النقطة. ولكن، كيف يُمكن استخدام المشتقة لدراسة تزايد الاقتران وتناقصه على مجاله ؟

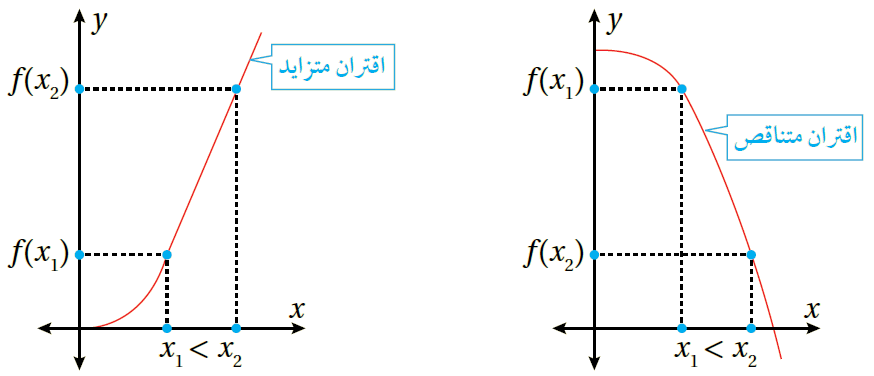
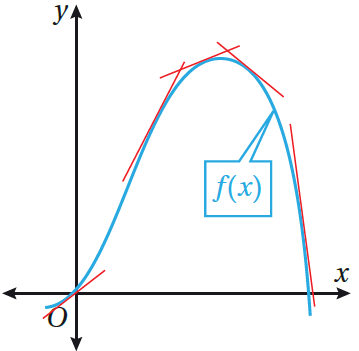
يُبيّن الشكل المجاور بعض مماسات منحنى الاقتران $y = f\left(x\right)$ أُلاحظ من الشكل أنّ :   · المماسات ذات الميل الموجب مرتبطة بالجزء المتزايد من منحنى الاقتران.        · المماسات ذات الميل السالب مرتبطة بالجزء المتناقص من منحنى الاقتران. ومن ثمّ ، يُمكن استعمال إشارة المشتقة لتحديد فترات التزايد والتناقص للاقتران.

 

 

 

 

 

 

 

 

 

نظرية 

• إذا كان $f\text{'}\left(x\right) > 0$ لقيم x  جميعها في الفترة I ، فإنّ الاقتران f  يكون متزايدً على الفترة I 

• إذا كان $f\text{'}\left(x\right) < 0$ لقيم x  جميعها في الفترة I ، فإنّ الاقتران f  يكون متناقصًا على الفترة I 

 

مثال : 

أحدد فترات التزايد والتناقص لكل اقتران مما ياتي :  

 

الحل : 

$\mathbf{1}\mathbf{)} f(x) = 3x^2- 12x+1$

الخطوة 1 : أجد مشتقة الاقتران ، ثم أجد أصفارها.

مشتقة الاقتران	$f\text{'}\left(x\right) = 6x -12$
بمساواة المشتقة بالصفر	$6x-12 = 0$
حل المعادلة الناتجة وإيجاد قيمة x	$6x = 12$ $x = 2$

إذن : صفر المشتقة هو  x = 2 

الخطوة 2 : أبحث في إشارة المشتقة حول أصفارها.

أختار قيمة أكبر من صفر المشتقة  (أيْ أكبر من 2) ، وقيمة أُخرى أصغر منها، ثم أختبر إشارة
المشتقة عند القيمتين :

$x > 2$		$x < 2$		القترة
$x = 3$		$x = 1$		قيم الاختبار (x)
$f\text{'}\left(3\right) > 0$		$f\text{'}\left(1\right) < 0$		إشارة $f\text{'}\left(x\right)$
متزايد		متناقص		سلوك الاقتران

 

 

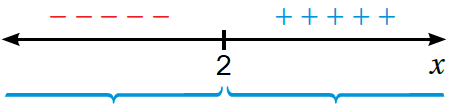
إذن : الاقتران f متناقص في الفترة $(-\infty , 2)$ ، ومتزايد في الفترة $(2 , \infty )$

---

f(x)=$\frac{1}{3}$  x³+ 2x²+3x

الخطوة 1 : أجد مشتقة الاقتران ، ثم أجد أصفارها.

$f\text{'}\left(x\right) = {\mathrm{x<sup>2</sup>}}^{}+ 4x +3$	مشتقة الاقتران
$x^{2 }+ 4x + 3 = 0$	بمساواة المشتقة بالصفر
$x^{2 }+ 4x + 3 = 0$ $$\begin{gathered} \mathrm{} \\ (x+1)(x+3) =0 \\ \Rightarrow x = - 1 , x = -3 \end{gathered}$$	حل المعادلة الناتجة (تحليل ثلاثي الحدود) وإيجاد قيم x

إذن : أصفار المشتقة هي : $x = - 1 , x = -3$  

الخطوة 2 : أبحث في إشارة المشتقة حول أصفارها.

$x > -1$		$-1>x>-3$$$		$x<-3$		الفترة
$x = 0$		$x = -2$		$x = -4$		(x) قيم الاختبار
$f\text{'}( 0) > 0$		$f\text{'}(-2) < 0$		$f\text{'}(-4) > 0$		$f\text{'}\left(x\right)$ إشارة
متزايد		متناقص		متزايد		سلوك الاقتران

 

إذن : الاقتران f متزايد في الفترتين $(-\infty , -3) , (-1 , \infty )$ ومتناقص في الفترة $(-3 , -1)$ 

---

 

•• يُمكن استعمال المشتقة لتصنيف النقاط الحرجة لكثيرات الحدود كما يأتي :

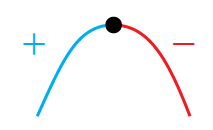
النقطة العظمى المحلية : نقطة حرجة يتزايد منحنى الاقتران عن يسارها، ويتناقص عن يمينها؛ ما يعني أنّ إشارة المشتقة تتغير من الموجب إلى  السالب عند الحركة من يسار النقطة إلى يمينها.
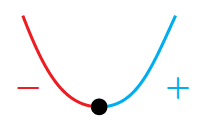
النقطة  صغرى المحلية : نقطة حرجة يتناقص منحنى الاقتران عن يسارها، ويتزايد عن يمينها؛ ما يعني  أنّ إشارة المشتقة تتغير من السالب إلى الموجب عند الحركة من يسار  النقطة إلى يمينها.

 

 

 

 

 

 

 

 

 

مثال : 

إذا كان الاقتران :  f(x)= $\frac{1}{3}$x³ - x  ، فاستخدم المشتقة لإيجاد كل مما يأتي : 

a)  النقاط الحرجة للاقتران h.
b) تصنيف النقاط الحرجة إلى عظمى محلية ، وصغرى محلية.

الحل : 

a)  النقاط الحرجة للاقتران h.

مشتقة الاقتران	$h\text{'}\left(x\right) = x^2 - 1$
مساواة المشتقة بالصفر	$x^2 - 1 = 0$
حل المعادلة الناتجة (تحليل فرق مربعين) وإيجاد قيم x	$x^2 - 1 = 0$ $$\begin{gathered} \mathrm{} \\ (x-1) (x+1) = 0 \\ \Rightarrow x = 1 , x = -1 \end{gathered}$$

إذن : أصفار المشتقة هي : $x = -1 , x = 1$

النقاط الحرجة : عند x = 1  ، فإنّ $h\left(1\right) = -\frac{2}{3}$   ، إذن النقطة الحرجة الأولى : $(1 , -\frac{2}{3})$

وعند x = -1  ، فإنّ  $h(-1) = \frac{2}{3}$  ، إذن النقطة الحرجة الثانية : $(-1 , \frac{2}{3})$  

---

b) تصنيف النقاط الحرجة إلى عظمى محلية ، وصغرى محلية.

$x > 1$	$-1<x<1$	$x< -1$	الفترة
$x = 2$	$x = 0$	$x = -2$	قيم الاختبار (x)
$h\text{'}( 2) > 0$	$h\text{'}( 0) < 0$	$h\text{'}(-2) > 0$	إشارة $h\text{'}\left(x\right)$
متزايد	متناقص	متزايد	سلوك الاقتران

 

 

إذن، النقطة $(-1 , \frac{2}{3})$ عظمى محلية ؛ لأنَّ الاقتران متزايد عن يسارها ومتناقص عن يمينها ، والنقطة $(-1 , \frac{2}{3})$ صغرى محلية ؛ لأنَّ الاقتران متناقص عن يسارها، ومتزايد عن يمينها.

---