التطابق

تذكير: درسْتُ سابقًا أنَّ الشكلَ الأصليَّ وَصورتَهُ تحتَ تأثيرِ التحويلاتِ الهندسيةِ (الدّورانِ، والانعكاسِ، والانسحابِ) لهما الشكلُ وَالمقاسُ نفسُهُما، إذنْ، فَهُما متطابقانِ، وبالتالي، يمكنُنا التحققُ مِنْ تطابقِ شكلَينِ بِإجراءِ انسحابٍ، أَوْ دَوَرانٍ، أَوِ انعكاسٍ لِاحدِهِما وَالتأكدِ مِنِ انطباقِهِ على الشكلِ الآخَرِ تمامًا

المضلعاتُ المتطابقةُ :مضلعاتٌ أجزائها المتقابلةُ متطابقةٌ، فَالأضلاعُ المتقابلةُ تُسمّى الأضلاعَ المتناظِرةَ وَالزوايا المتقابلةُ تُسمّى الزوايا المتناظِرةَ ويُستعمَلُ الرمزُ (≅) للدلالةِ على أنَّ الشكلَينِ متطابقانِ. 

مفاهيم أساسية 

يكونُ المضلعانِ متطابقَينِ إذا كانَتِ الأضلاعُ المتناظِرةُ متطابقةً وَالزوايا المتناظِرةُ متطابقةً.

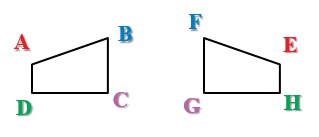
إذا كانَ ABCD ≅ EFGH فإنَّ:

∠A ≅ ∠E, ∠B ≅ ∠F, ∠C ≅ ∠G, ∠D ≅ ∠H: الزوايا المتطابقةَ

$\overline{\mathrm{AB}} \cong \overline{ \mathrm{EF} },\overline{ \mathrm{BC}} \cong \overline{\mathrm{FG}} , \overline{\mathrm{CD}} \cong \overline{\mathrm{GH} }, \overline{\mathrm{DA}} \cong \overline{\mathrm{HE}}$: وَالأضلاعَ المتطابقةَ

 

مثال 1:أكتبُ جُملَ التطابقِ لِكلٍّ مِنْ أزواجِ المضلعاتِ المتطابقةِ الآتيةِ:

1)

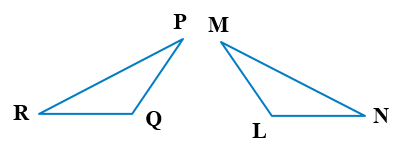
الْخُطْوَةُ 1: استخدم عددًا متساويًا مِنَ الأقواسِ لِلدلالةِ على الزوايا المتناظرةِ المتطابقةِ، وَعددًا متساويًا مِنَ الخطوطِ الصغيرةِ لِلدلالةِ على الأضلاعِ المتناظرةِ المتطابقة.

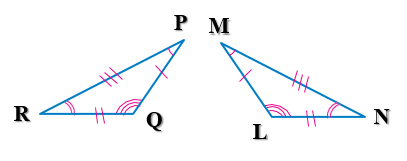
الْخُطْوَةُ 2: أكتبُ جُمَلَ التطابقِ 

∠M ≅ ∠P, ∠L ≅ ∠Q, ∠N ≅ ∠R: الزوايا المتناظرةُ

$\overline{\mathrm{ML} }\cong \overline{\mathrm{PQ}} , \overline{\mathrm{LN}} \cong \overline{ \mathrm{QR}} ,\overline{ \mathrm{MN}} \cong \overline{\mathrm{PR}}$: الأضلاعُ المتناظرةُ

 

يُمكنُني استخدامُ خواصِّ تطابقِ المضلعاتِ لِايجادِ قياساتِ زوايا وَأضلاعٍ مجهولةٍ.

مثال 2: في الشكلِ المجاورِ إذا كانَ FCDE ≅ NOPM وَكانَ °CD = 7 cm، m∠P = 104

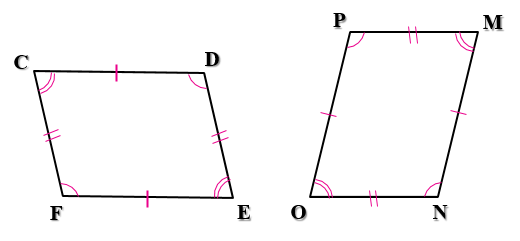
1) قياسَ$\angle D$

  متناظرتانِ في مضلعَينِ متطابقَينِ، ∠P وَ ∠D بما أنَّ

m∠D = إذنْ، فَهُما متطابقتانِ. وَمنهُ ° 104

2) طول $\overline{\mathbf{OP}}$

بِما أنَّ $\overline{\mathrm{OP}}$ و$\overline{\mathrm{CD}}$  متناظرانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقانِ. ومنه OP=7cm

 

يمكنُ استعمالُ مجموعِ قياساتِ زوايا المضلعِ في إيجادِ زوايا مفقودةٍ.

مثال3: في الشكلِ المجاورِ: ΔWYS ≅ ΔMKV  أَجِدُ m∠V

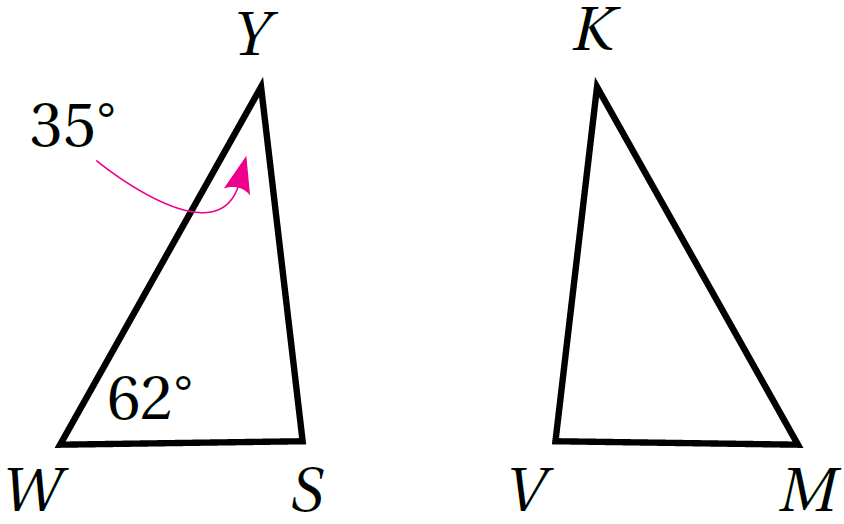
m∠S الْخُطْوَةُ 1: أَجِدُ قياسَ الزاويةِ

$\mathrm{m}\angle \mathrm{Y} + \mathrm{m}\angle \mathrm{W} + \mathrm{m}\angle \mathrm{S} ={180}^{°}$                مجموعُ قياساتِ زوايا المثلثِ 

$35° + 62° + \mathrm{m}\angle \mathrm{S} = 180°$                        أعوّضُ $\mathrm{m}\angle \mathrm{W}={62}^{°}$ و $m\angle Y={35}^{°}$

$97° + m\angle S = {180}^{°}$                                   أجمعُ    

$\mathrm{m}\angle \mathrm{S} = {83}^{°}$                                                 أطرحُ ° 97 مِنَ الطرفَينِ 

الْخُطْوَةُ 2: أستخدمُ خواصَّ المثلثاتِ المتطابقةِ.

m∠V = متناظرتانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقتانِ، وَمِنْهُ ° 83 ∠S وَ ∠V بِما أنَّ

 

يمكنُ استعمالُ المعادلاتِ في إيجادِ قياساتِ زوايا وَأضلاعٍ مجهولةٍ في المضلعاتِ المتطابقِة.

مثال4: في الشكلِ المجاورِ ABCD ≅ PQRS أَجِدُ:

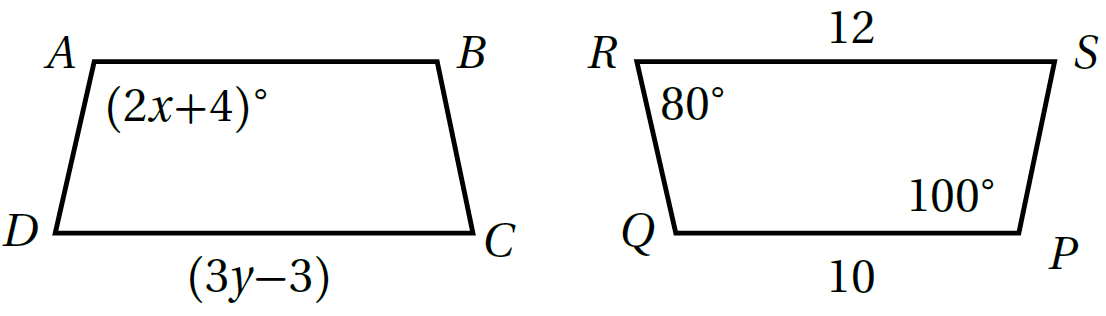
1) قيمة المتغير x

 بما أنَّ $\angle \mathrm{A}, \angle \mathrm{P}$ متناظرتانِ في شكلَينِ متطابقَينِ، إذنْ ${\left(2\mathrm{x}+4\right)}^{°}={100}^{°}$

100=2x+4                                                    أكتبُ المعادلةَ 

2x=96                                                          أطرح 4 من الطرفين 

$$\begin{gathered} \frac{2\mathrm{x}=96}{÷2 ÷2} \\ \mathrm{x}=48 \end{gathered}$$                                                  بقسمة الطرفين على 2 نجد قيمة x