رياضيات فصل ثاني

حلول أسئلة أتحقق من فهمي

2)

  

الْخُطْوَةُ 1 : استخدم عددًا متساويًا مِنَ الأقواسِ لِلدلالةِ على الزوايا المتناظرةِ المتطابقةِ، وَعددًا متساويًا مِنَ الخطوطِ الصغيرةِ لِلدلالةِ على الأضلاعِ المتناظرةِ المتطابقة.

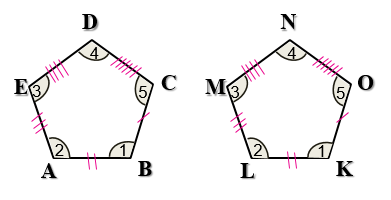
الْخُطْوَةُ 2: أكتبُ جُمَلَ التطابقِ  

∠A ≅ ∠L , ∠B ≅ ∠K , ∠C ≅ ∠O , ∠D ≅ ∠N , ∠E ≅ ∠M الزوايا المتناظرة

الأضلاع المتناظرة $\overline{\mathrm{AB} }\cong \overline{\mathrm{LK}} , \overline{\mathrm{BC} }\cong \overline{\mathrm{KO}} , \overline{\mathrm{CD} }\cong \overline{\mathrm{ON}} , \overline{\mathrm{DE}} \cong \overline{ \mathrm{NM}} , \overline{\mathrm{EA} }\cong \overline{ \mathrm{ML}}$

3)

الْخُطْوَةُ 1 : أستخدمُ عددًا متساويًا مِنَ الأقواسِ لِلدلالةِ على الزوايا المتناظرةِ المتطابقةِ، وَعددًا متساويًا مِنَ الخطوطِ الصغيرةِ لِلدلالةِ على الأضلاعِ المتناظرةِ المتطابقة.

 

 

 

 

 

 

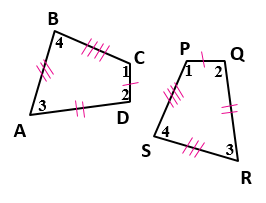
الْخُطْوَةُ 2: أكتبُ جُمَلَ التطابقِ  

 ∠A ≅ ∠R , ∠B ≅ ∠S , ∠C ≅ ∠P , ∠D ≅ ∠Q الزوايا المتناظرة

الأضلاع المتناظرة: $\overline{\mathrm{AB}} \cong \overline{\mathrm{RS}} , \overline{\mathrm{BC} }\cong \overline{\mathrm{SP} }, \overline{\mathrm{CD}} \cong \overline{\mathrm{PQ}} , \overline{\mathrm{DA}} \cong \overline{\mathrm{QR}}$

 

 

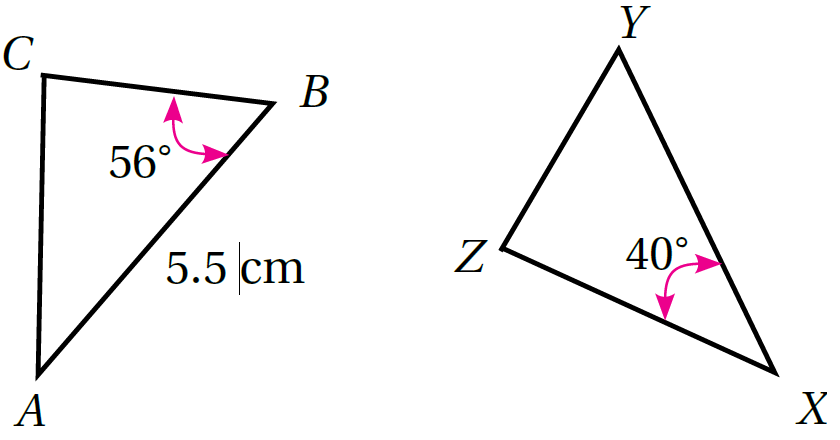
3)قياس$\mathbf{\angle }\mathbf{A}\mathbf{ }$

بما أنَّ $\angle \mathrm{A} ,\angle \mathrm{X}$ متناظرتانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقتانِ. وَمنهُ $\angle \mathrm{A} ={40}^{°}$m

4) طول $\overline{\mathbf{XY}}$

بما أنَّ $\overline{\mathrm{XY}},\overline{\mathrm{AB}}$  متناظرانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقانِ.وَمنهُ XY=5.5cm

 

2)في الشكل المجاور ΔCAB ≅ ΔZXY أَجِدُ $\mathbf{m}\mathbf{\angle }\mathbf{A}\mathbf{ }$

$$\begin{gathered} \mathrm{m}\angle \mathrm{X}+ \mathrm{m}\angle \mathrm{Y}+ \mathrm{m}\angle \mathrm{Z} ={180}^{°} \\ \mathrm{m}\angle \mathrm{X} +66°+35°=180° \end{gathered}$$                        مجموع زوايا المثلث = 180 درجة 

$$\begin{gathered} \mathrm{m}\angle \mathrm{X}+101°=180° \\ \mathrm{m}\angle \mathrm{X}=79° \end{gathered}$$

 

 

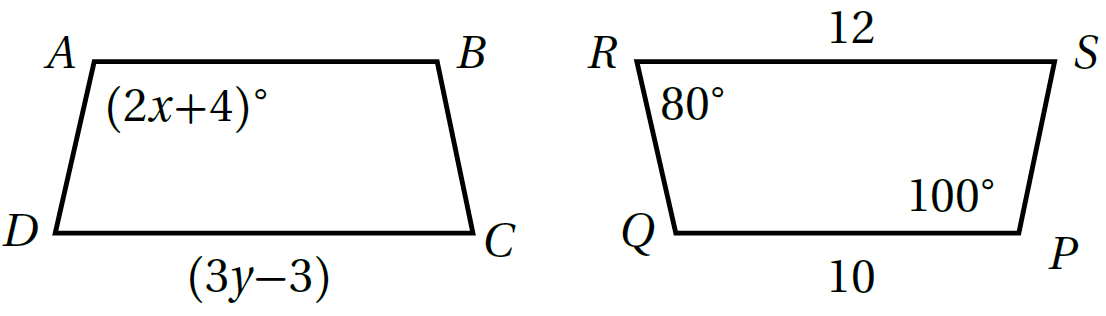
2) قيمة المتغير y

بما أنَّ $\overline{\mathrm{DC}},\overline{\mathrm{SR}}$  ضلعين متناظرتانِ في شكلَينِ متطابقَينِ فإن 12=3-3y

بحل المعادلة 

$$\begin{gathered} 3\mathrm{y}-3=12 \\ 3\mathrm{y}=15 \\ \mathrm{y}=5 \end{gathered}$$

---

حلول أسئلة أتدرب وأحل المسائل 

أكتبُ جُمَلَ التطابقِ لِكلٍّ مِنْ أزواجِ المضلعاتِ المتطابقةِ الآتيةِ:

1)

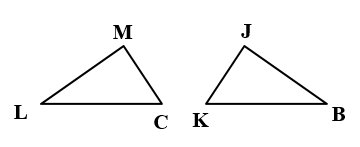
الْخُطْوَةُ 1 : أستخدمُ عددًا متساويًا مِنَ الأقواسِ لِلدلالةِ على الزوايا المتناظرةِ المتطابقةِ، وَعددًا متساويًا مِنَ الخطوطِ الصغيرةِ لِلدلالةِ على الأضلاعِ المتناظرةِ المتطابقة.

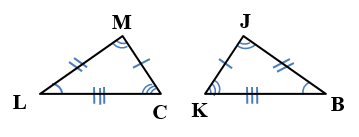
الْخُطْوَةُ 2: أكتبُ جُمَلَ التطابقِ  

∠C ≅ ∠K , ∠L ≅ ∠B , ∠M ≅ ∠J الزوايا المتناظرة

الأضلاع المتناظرةُ: $\overline{\mathrm{CL}}\cong \overline{\mathrm{KB}} , \overline{\mathrm{LM}}\cong \overline{\mathrm{BJ}} , \overline{\mathrm{MC}}\cong \overline{\mathrm{JK}}$

 

2)

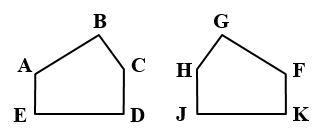
الْخُطْوَةُ 1 : أستخدمُ عددًا متساويًا مِنَ الأقواسِ لِلدلالةِ على الزوايا المتناظرةِ المتطابقةِ، وَعددًا متساويًا مِنَ الخطوطِ الصغيرةِ لِلدلالةِ على الأضلاعِ المتناظرةِ المتطابقة.

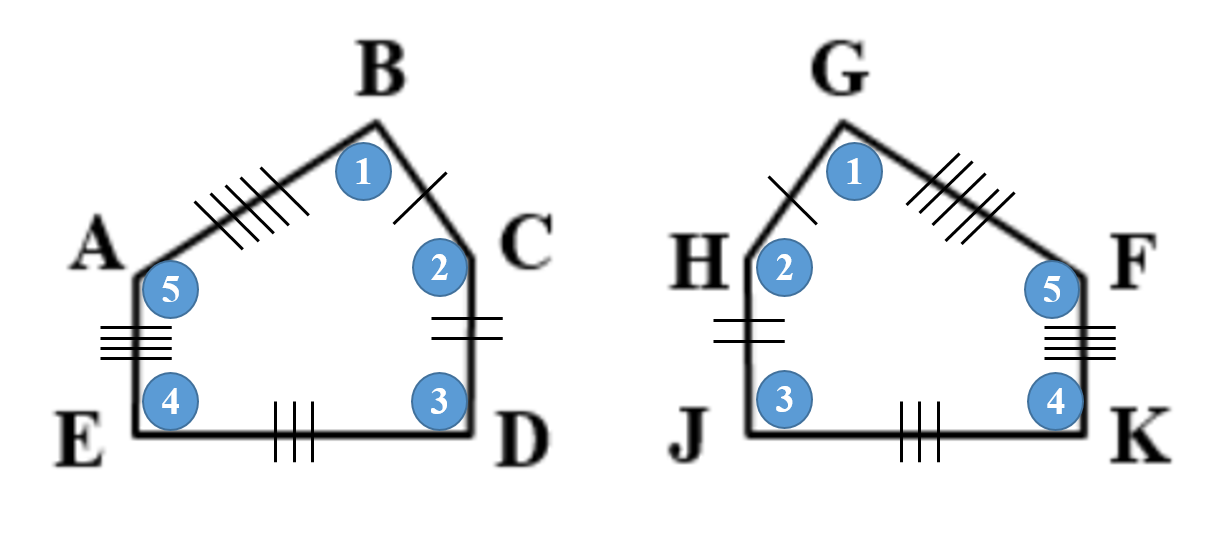
الْخُطْوَةُ 2: أكتبُ جُمَلَ التطابقِ  

∠B ≅ ∠G , ∠C ≅ ∠H, ∠D ≅ ∠J ,∠E ≅ ∠K , ∠A ≅ ∠F , الزوايا المتناظرة

الأضلاع المتناظرةُ: $\overline{\mathrm{BC}}\cong \overline{\mathrm{G}}\mathrm{H} ,\overline{\mathrm{CD}}\cong \overline{\mathrm{HJ}} , \overline{\mathrm{D}}\mathrm{E}\cong \overline{\mathrm{JK}} ,\overline{\mathrm{EA}}\cong \overline{\mathrm{KF}} , \overline{\mathrm{AB}}\cong \overline{\mathrm{FG}}$

 

إشاراتُ مرورٍ: يبيّنُ الشكلُ المجاورُ إشارتَيْ مرورٍ متطابقتَينِ، إذا كانَ $\mathbf{m}\mathbf{\angle }\mathbf{Y}\mathbf{=}{\mathbf{60}}^{\mathbf{°}}\mathbf{,}\mathbf{ }\mathbf{ZX}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{55}\mathbf{ }\mathbf{cm}$ فَأَجِدُ:

 

 

 

 

 

3)قياسَ $\mathbf{\angle }\mathbf{S}$

بما أنَّ $\angle \mathrm{S}, \angle \mathrm{Y}$ متناظرتانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقتانِ. وَمنهُ $\mathrm{m}\angle \mathrm{S}={60}^{°}$

4) طولَ $\overline{\mathbf{TR}}$

بما أنَّ  $\overline{\mathrm{TR}},\overline{\mathrm{ZX}}$ متناظرانِ في مضلعَينِ متطابقَينِ، إذنْ، فَهُما متطابقانِ.وَمنهُ TR=55 cm 

 

يبيّنُ الشكلُ الآتي مضلعًا سداسيًّا منتظمًا مقسَّمًا إلى 17 مثلثًا:

 

 

 

 

 

 

 

 

 

 

 

5) أحدّدُ المثلثاتِ جميعَها المتطابقةَ معَ المثلثِ C

Q المثلث ، M المثلث ، B المثلث

6) أيُّ المثلثاتِ يتطابقُ معَ المثلثِ D

P المثلث

7) أيُّ المثلثاتِ يطابقُ المثلثَ H

المثلث K ، المثلث I

 

 أَجِدُ: ، ΔABC ≅ ΔNML في الشكلِ المجاورِ

 

 

 

 

 

 

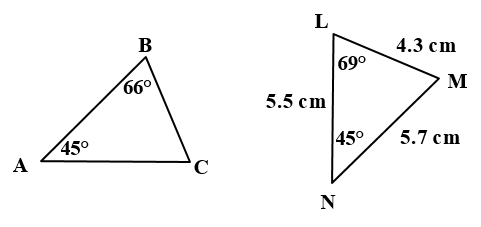
8) قياس $\mathbf{\angle }\mathbf{M}$

مجموع زوايا المثلث = 180 درجة

$$\begin{gathered} \angle \mathrm{M} = 180-(69+45) \\ \angle \mathrm{M} = {66}^{°} \end{gathered}$$

أو من تطابق $\angle \mathrm{M} , \angle \mathrm{B}$

9) طول $\overline{\mathbf{BC}}$

$\overline{\mathrm{BC}},\overline{\mathrm{ML}}$ متطابقان ومنه BC=4.3cm

10)طول $\overline{\mathbf{AB}}$

$\overline{\mathrm{AB}},\overline{\mathrm{NM}}$ متطابقان ومنه BC=5.7cm

 

فَأَجِدُ: ، ABCD ≅ ZWXY في الشكلِ المجاورِ

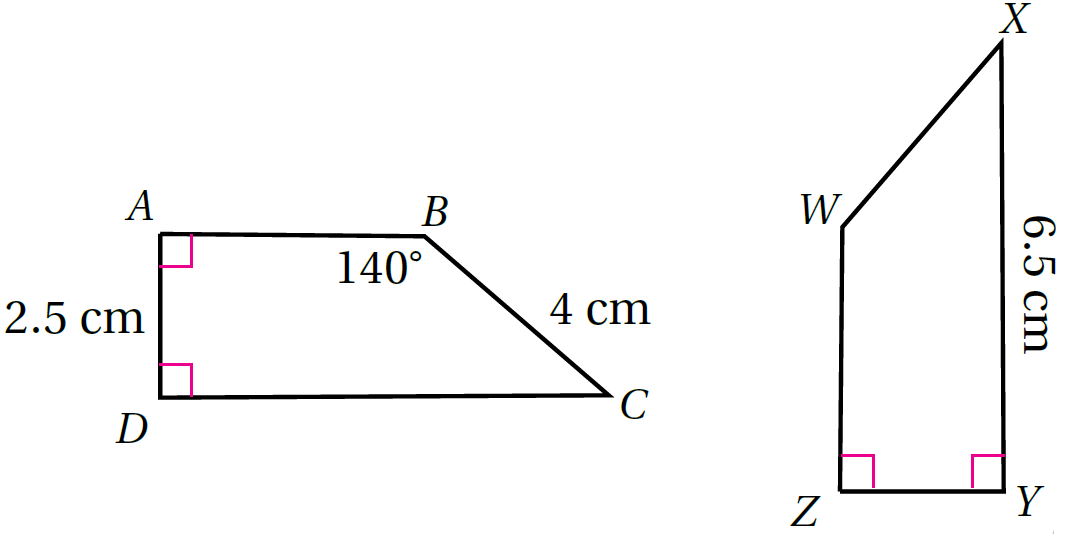
11) طول $\overline{\mathbf{WX}}$

$\overline{\mathrm{WX}},\overline{\mathrm{BC}}$  متطابقان ومنه WX=4cm

12) قياس $\mathbf{\angle }\mathbf{W}$

$\angle \mathrm{W} ,\angle \mathrm{B}$ متطابقتان ومنه $\angle \mathrm{W}={140}^{°}$

13) قياس $\mathbf{\angle }\mathbf{X}$

مجموع الزوايا في الشكل الرباعي = 360 درجة ومنه يمكن ايجاد قياس الزاوية X

$$\begin{gathered} \angle \mathrm{X}=360 - (\angle \mathrm{Y}+\angle \mathrm{Z}+\angle \mathrm{W}) \\ =360-(90+90+140) \\ ={40}^{°} \end{gathered}$$

14) في الشكلِ الآتي إذا كانَ ABCD ≅ EFGH فأَجِدُ قيمةَ كلٍّ مِنَ المتغيِّرَينِ x,y

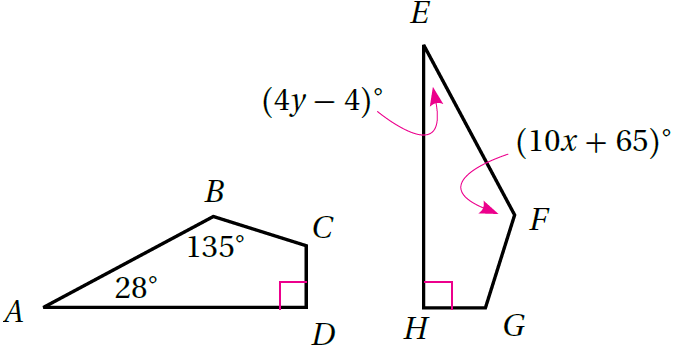
ايجاد قيمة x

$$\begin{gathered} \mathrm{m}\angle \mathrm{B}\cong \mathrm{m}\angle \mathrm{F} \\ {(10\mathrm{x}+65)}^{°}={135}^{°} \\ 10\mathrm{x}=70 \\ \mathrm{x}=7 \end{gathered}$$                           من تطابق الزاويتين B,F نعوض في المعادلة لايجاد x

ايجاد قيمة y

$$\begin{gathered} \mathrm{m}\angle \mathrm{A}\cong \mathrm{m}\angle \mathrm{E} \\ {(4\mathrm{y}-4)}^{°}={28}^{°} \\ 4\mathrm{y}=32 \\ \mathrm{y}=8 \end{gathered}$$                                  من تطابق الزاويتين A,E نعوض في المعادلة لايجاد y

15) تبريرٌ: في الشكلِ المجاورِ إذا كانَ ABCM ≅ XYKM فَأَجِدُ $\mathbf{m}\mathbf{\angle }\mathbf{KMC}$ مبررًا إجابتي.

 

 

 

 

 

 

 

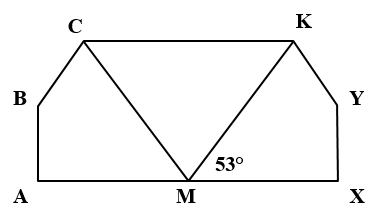
m∠XMK = m∠AMC = 53°                           من التطابق

m∠XMK+m∠KMC+m∠AMC = 180°  قياس الزاوية المستقيمة

53° + m∠KMC + 53° = 180°                                 أعوض

106° + m∠KMC = أجمع                                  ° 180

m∠KMC = 180°-106° = أحل المعادلة                       ° 74

m∠KMC = 74° اذن

 

16)أكتشفُ الخطأَ: أحدّدُ الخطأَ في الحلِّ الآتي، وَأصححُهُ:

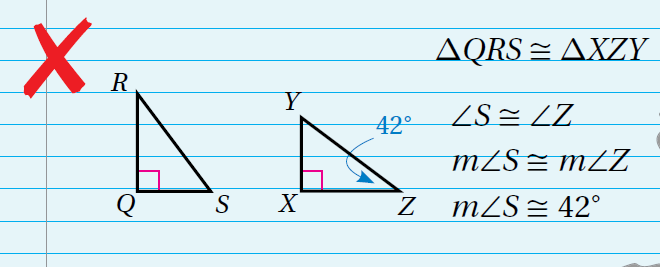
 العبارة خاطئة  ∠S ≅ ∠Z

 العبارة الصحيحة ∠S ≅ ∠Y

m∠Y=180°-(90°+42°) = 48°

m∠S = إذن : ° 48

 

17) تحدٍّ: في ما يلي وصفٌ للمثلثَينِ ΔABC و ΔZXW قائمَيِ الزاوية:

ΔZXW	ΔABC
طولُ الوتَرِ 10cm	طولُ الوتَرِ 10cm
وَقياسا زاويتَينِ فيهِ${25}^{°},{65}^{°}$	طولُ أحدِ أضلاعِهِ 6cm

أحدّدُ ما إذا كانَ المثلثانِ  ΔABC و ΔZXW متطابقَينِ، مبررًا إجابتي.

نجد طول الضلع الثالث في المثلث قائم الزاوية ABC باستخدام قانون فيثاغورس 

$$\begin{gathered} 10=\sqrt{{\left(6\right)}^2+{\left(\mathrm{x}\right)}^2} \\ \mathrm{x}=8 \mathrm{cm} \end{gathered}$$

باستخدام النسب المثلثية في المثلث نجد الزوايا 

$$\begin{gathered} \sin {\left(\frac{6}{10}\right)}^{-1}=36.8^{°} \\ \cos {\left(\frac{6}{10}\right)}^{-1}=53.1^{°} \end{gathered}$$

قياس الزوايا غير متساوي لأي حالة اذن المثلثين غير متطابقين 

 

18) أكتبُُ: كيفَ أحدّدُ ما إذا كانَ مضلعانِ متطابقينِ أَمْ لا؟

أقارن الأضلاع المتناظرة والزوايا المتناظرة فإذا تساوت أطوال الأضلاع المتناظرة وتساوت قياسات الزوايا المتناظرة يكون المضلعان متطابقين.

---

---

حلول أسئلة كتاب التمارين 

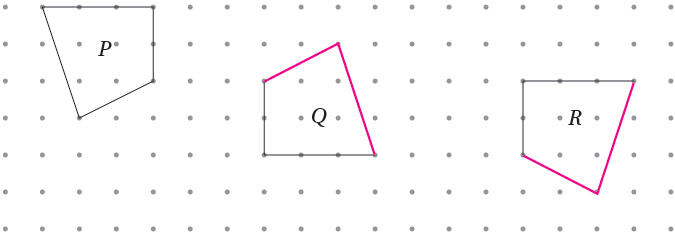
1) إذا كانَتِ الأشكالُ P و Q و R متطابقةً، أُكملُ الشكلَينِ Q و R

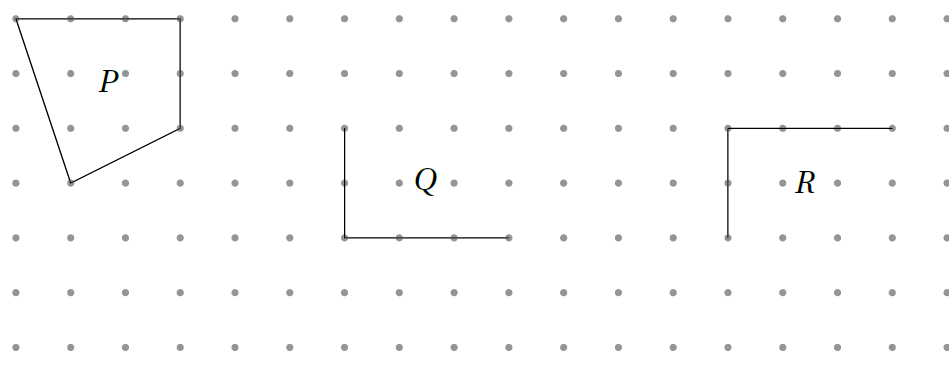
الحل : 

 

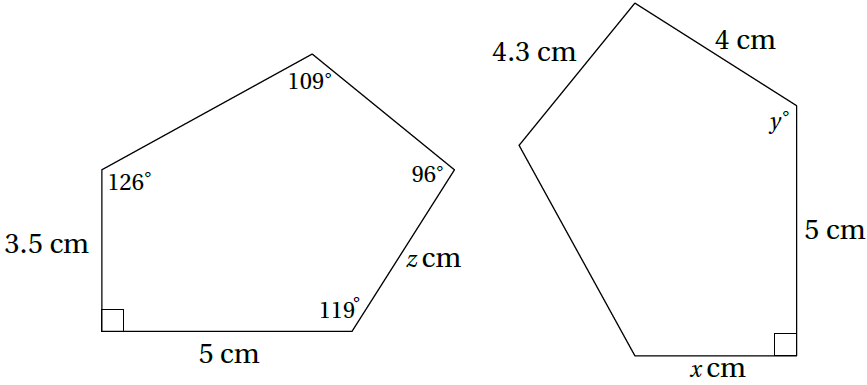
2)يبيّنُ الشكلُ المجاورُ مضلّعَينِ متطابقَينِ، أَجِدُ قيمةَ كلٍّ مِنْ x,y,z 

الحل :

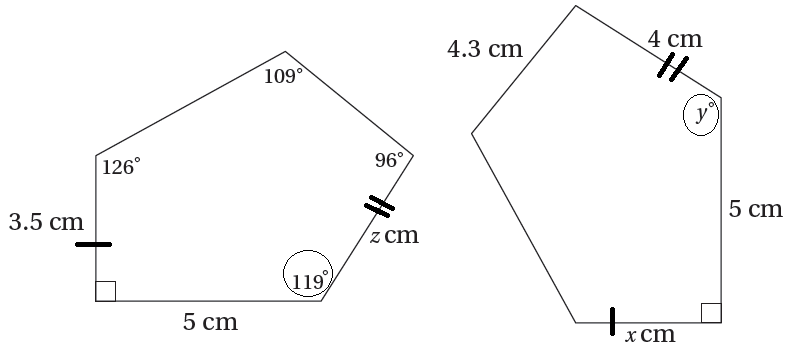
من التطابق : x = 3.5 , y = 119°, z = 4

 

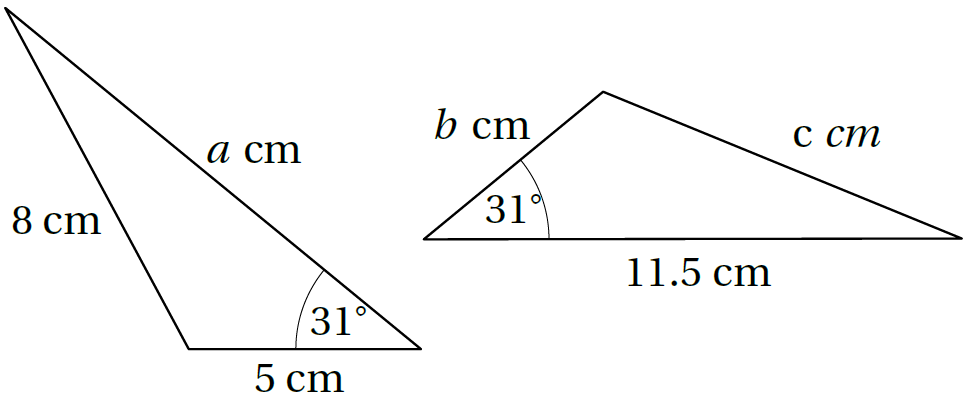
3) يبيّنُ الشكلُ الآتي مثلَّثَينِ متطابقَينِ، أَجِدُ قيمةَ كلٍّ مِنْ a,b,c

الحل:

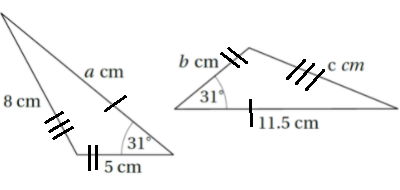
من التطابق: a = 11.5 , b = 5 , c = 8

 

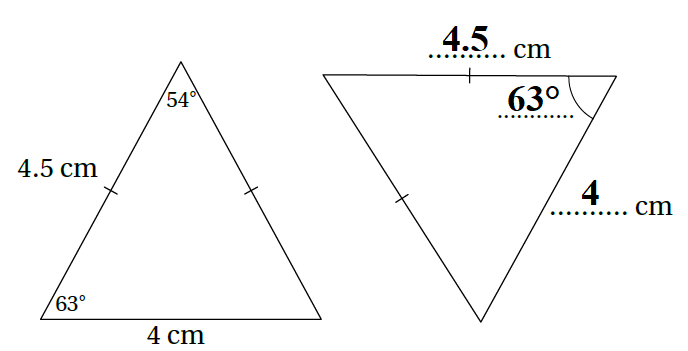
4) يبيّنُ الشكلُ الآتي مثلَّثَينِ متطابقَينِ كلٌّ مِنْهُما متساوِي الساقَينِ. أَجِدُ القياساتِ المجهولةَ في الشكلِ:

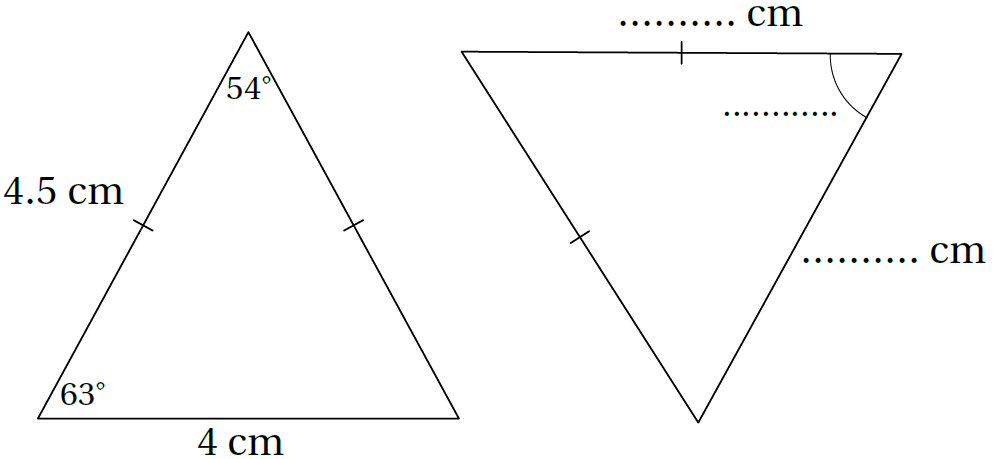
الحل:

 

أيُّ الجُملِ الآتيةِ صحيحةٌ وَأيُّها خطأٌ؟ أبرّرُ إجابتي. ، ΔABC ≅ ΔRQP في الشكلِ المجاورِ

 

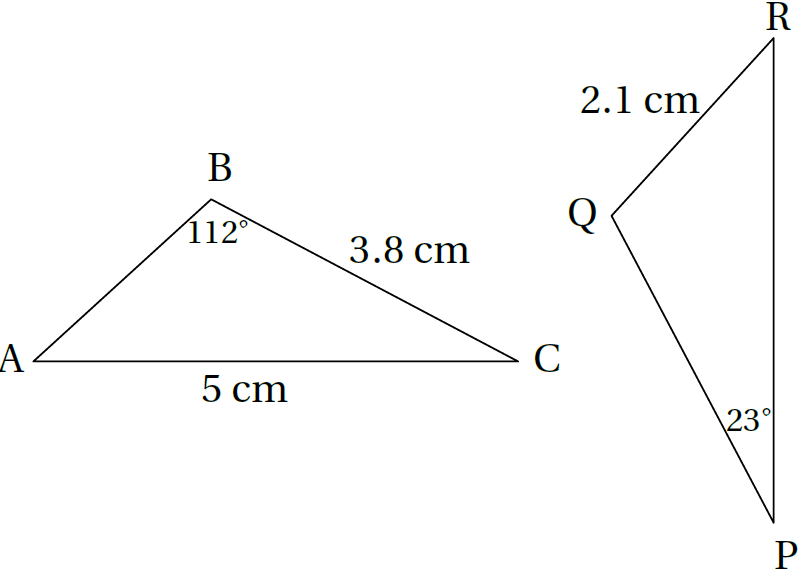
5)m∠BAC = 23°

الحل: العبارة خطأ لأن نظير $\angle \mathrm{BAC}$ هي $\angle \mathrm{QRP} = 180-(112+23) = {45}^{°}$ 

6) PQ = 5 cm

الحل:العبارة خطأ لأن نظير PQ هي CB=3.8cm وليست AC 

7) m∠PQR =112°

الحل: العبارة صحيحة لأن الزاويتان $\angle \mathrm{PQR} \cong \angle \mathrm{CBA}$

 

8) أيُّ المثلَّثاتِ الآتيةِ يطابقُ المثلَّثَ T أبرّرُ إجابتي.

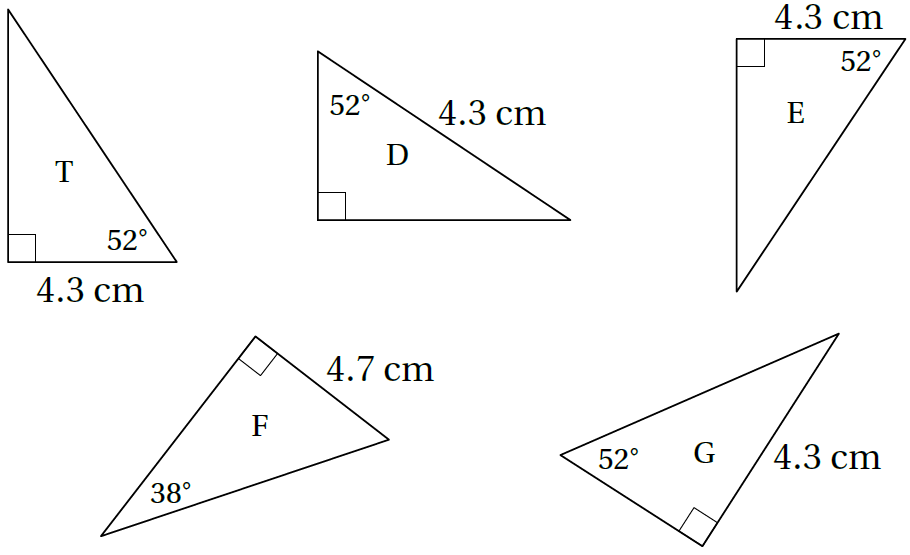
الحل: المثلث E لأن العناصر المتناظرة متطابقة

 

9) أكتشفُ الخطأَ: تقولُ هديلُ: إِنَّ المثلَّثَينِ الآتيَينِ متطابقانِ. هلْ ما قالَتْهُ هديلُ صحيحٌ؟ أبرّرُ إجابتي.

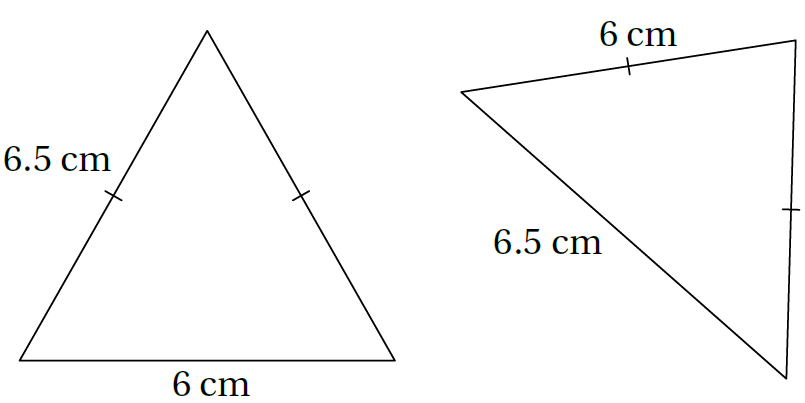
الحل: خطأ لأن طول كل من الضلعين المتطابقين في المثلث الأيمن = 6cm  بينما طول كل من الضلعين المتطابقين في المثلث الأيسر = 6cm

 

تبريرٌ: أعطي سببًا واحدًا على الأقلِّ لِعدمِ صحةِ كلِّ جُملةٍ في ما يأتي:
10) المربَّعاتُ متطابقةٌ دائمًا؛ لِنَّ زواياها متطابقةٌ.

الحل: يمكن أن نرسم مربعين أطوال اضلاعهما غير متطابقة (شرط الاضلاع المتناظرة غير متحقق في هذه الحالة)

11)شكلانِ رباعيّانِ، طولُ كلِّ ضلعٍ فيهما 4cm إذنْ، هُما متطابقانِ.

الحل:يمكن أن يكون أحدهما مربع والآخر معين غير قائم الزوايا. (شرط الزوايا المتناظرة غير متحقق في هذه الحالة)