رياضيات 7 فصل ثاني

مفهوم أساسي: 

تمثّلُ العلاقةُ بينَ الكمّيتَينِ المتغيّرتَينِ x,y  تغيرًا طرديًّا إذا كانَتِ النسبةُ بينَ جميعِ قِيَمِهِما ثابتةً ولتكن k حيثُ , k ≠0  بحيثُ تؤدي الزيادةُ في إحدى الكمّيتَينِ إلى زيادةِ الأُخرى وكذلكَ العكسُ ، و يُسمّى k ثابتَ التغير (Constant of variation) وهو يمثل معدل الوحدة 

التغير الطرديُّ (Direct variation) هُوَ علاقةٌ بينَ المتغيرَينِ x,y  تكونُ فيها النسبةُ y : x ثابتةً

 $\mathbf{k}=\frac{\mathrm{y}}{\mathrm{x}}$ حيث k ≠0 

وَتمثّلُ المعادلةُ y = k x معادلةَ التغير الطرديِّ.

 

مثال 1: يمثّلُ الجدولُ المجاورُ علاقةً بينَ المتغيّرَينِ x,y 

y	x
8	1
16	2
24	3
??	10

1) أبين أن العلاقة بين x و  y تمثل تغيّرًا طرديًا، ثم أجد ثابت التغير .k

أَجِدُ النسبةَ $\frac{\mathrm{y}}{\mathrm{x}}$ لِلقيمِ المتناظرةِ جميعِها

$\frac{\mathrm{y}}{\mathrm{x}} \Rightarrow \frac{8}{1}=8 , \frac{16}{2} = 8 , \frac{24}{3} = 8$

النسبةُ y : x  ثابتةً ، اذن تمثل العلاقة بين y,x  تغيّرًا طرديًا، وثابتُ التغير k=8

2) أكتبُ معادلةَ التغير الطرديِّ، ثم أَجِدُ القيمةَ المجهولةَ في الجدولِ 

     $\mathrm{y}=8\mathrm{x}$                أكتبُ معادلةَ التغير الطرديِّ

   $\mathrm{y}=8\left(10\right)$               أُعوّضُ X=10 في المعادلةِ

        $\mathrm{y}=80$              أَجِدُ الناتجَ

 

مثال 2: منَ الحياةِ يمثّلُ الجدولُ المجاورُ علاقةَ تناسُبٍ بينَ عددِ السيّاراتِ في محطةِ غسيلٍ  للسيّاراتِ وَالمبلغِ المستحَقِّ مقابلَ تقديمِ الخدمةِ:

المبلغ JD	عدد السيارات
20	5
40	10
60	15
80	20

1) أبيّنُ أنَّ العلاقة بين عددَ السيّاراتِ والمبلغَ تمثل تغيرًا طرديًّا، ثمَّ أَجِدُ ثابتَ التناسُبِ K

$\frac{\mathrm{المبلغ}}{\mathrm{السيارات} \mathrm{عدد} } \Rightarrow \frac{20}{5}=4 , \frac{40}{10} = 4 , \frac{60}{15} = 4 , \frac{80}{20} = 4$

.k = النسبةُ بينَ جميعِ القِيَمِ ثابتةٌ، إذنْ، العلاقة بين المبلغُ وعددُ السيّاراتِ تمثل علاقة تغير طرديّ، وثابتُ التغير 4

2) أكتبُ معادلةَ التغير الطرديِّ.

y = 4x

يُمكنُنا إيجادُ ثابتِ التغير لعلاقةِ تغير طرديٍّ ممثَّلةٍ بيانيًّا:

1) بتحديدِ قيمةِ y عندَما تكونُ x=1 

2) إيجادِ معدَّلِ الوحدةِ لأيِّ نقطةٍ على التمثيلِ البيانيِّ.

 

مثال 3: يبيّنُ التمثيلُ البيانيُّ المجاورُ العلاقةَ بينَ الزمنِ بالدقائقِ والسُّعراتِ الحراريةِ الّتي يحرقُها شخصٌ في أثناءِ ممارستِهِ التمارينَ الرياضيةَ:
1) أبيّنُ أنَّ العلاقةَ تمثّلُ تغيرًا طرديًّا.
تمثّلُ العلاقةُ في التمثيلِ البيانيِّ المجاورِ علاقةَ تغير طرديٍّ؛ لأنَّ النقاطَ الممثَّلةَ تقعُ على مستقيمٍ يمرُّ بنقطةِ الأصلِ.

2) أَجِدُ ثابتَ التغير k

الطريقةُ 1: لإيجادِ ثابتِ التغير k أحددُ قيمةَ y عندَما x=1

إذنْ، ثابتُ التغير k=10 

الطريقةُ 2: أختارُ النقطةَ (2,20)  ثمَّ أَجِدُ منها ثابتَ التغير k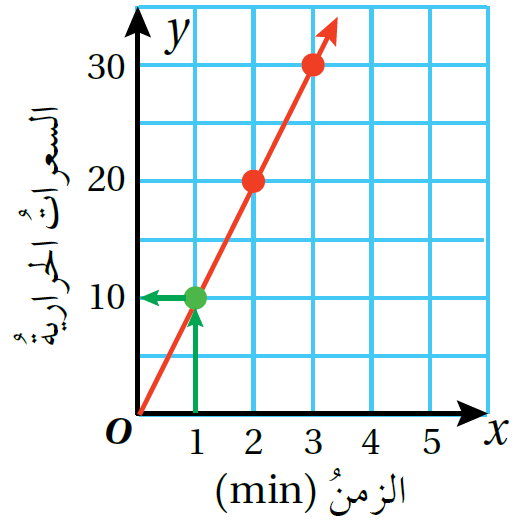        

$k=\frac{y}{x}$             أكتبُ معادلةَ التغير الطرديِّ

$=\frac{20}{2}$k           أُعوّضُ y=20 , x=2

k=10            أَجِدُ الناتجَ

3) أكتبُ معادلةَ التغير الطرديِّ.

y=10x 

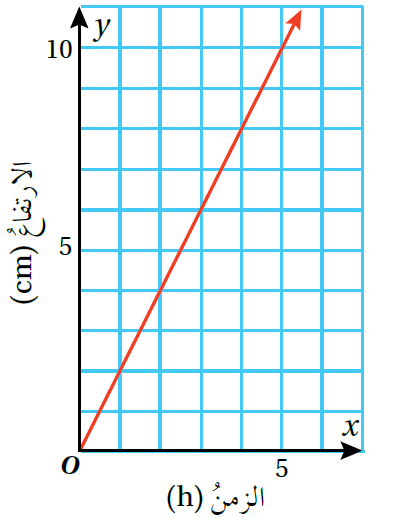
مثال 4: منَ الحياةِ رُصِدَ ارتفاعُ الثلوجِ على قمةِ أحدِ الجبالِ في أثناءِ عاصفةٍ ثلجيةٍ،فَوُجدَ أنَّهُ يزدادُ بمقدارِ 2cm  كلَّ ساعةٍ

1) أمثّلُ العلاقةَ بيانيًّا.
أُنشئُ جدولً، وأكتبُ النِّسَبَ فيهِ على شكلِ أزواجٍ مرتَّبةٍ:

الزمن (h)	1	2	3	4
ارتفاع الثلوج (cm)	2	4	6	8

(1 , 2), (2 , 4), (3 , 6), (4 , الأزواجُ المرتبةُ: ( 8

2) أبيّنُ أنَّ العلاقةَ تمثّلُ تغيرًا طرديًّا.
تمثّلُ العلاقةُ تغيرًا طرديَّا؛ لأنَّ النقاطَ الممثِّلةَ لها تقعُ على مستقيمٍ يمرُّ بنقطةِ الأصلِ.
3)أكتبُ معادلةَ التغير الطرديِّ.

بما أنَّ العلاقةَ تمثل علاقة تغير طرديٌّ، إذنْ، يُمكنُ إيجادُ معادلةٍ لها. وباستخدامِ النقطةِ (1,2) نجدُ أنَّ ثابتَ التناسُبِ k=2 

إذنْ، المعادلة y=2x         

4)أَجِدُ ارتفاعَ الثلجِ بعدَ مرورِ 10 ساعاتٍ

$\mathrm{y}=2\times 10$               أعوض x=10 

y=20                       أَجِدُ الناتجَ  

20 cm إذنْ، ارتفاعُ الثلجِ بعدَ مرورِ 10 ساعاتٍ هُوَ