رياضيات فصل ثاني

اجابات أسئلة أتحقق من فهمي 

أقسمُ مبلغَ 1400JD بينَ سُهى وجميلٍ بنسبةٍ 3:7 

$3+7=10$                  أَجِدُ عددَ الأجزاءِ جميعِها  

$\frac{1400}{10}=140\mathrm{JD}$        أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

ولإيجادِ المبلغ الّذي سيحصلُ عليْهِ كلٌّ مِنْ سُهى وجميلٍ؛ أَضربُ النسبةَ الخاصةَ بكلٍّ منهُما في حصة الجزءِ الواحدِ:

$3\times 140=420\mathrm{JD}\hspace{0.17em}$     نصيب سهى من المبلغ 420JD

$7\times 140=980\mathrm{JD}\hspace{0.17em}$     نصيب جميل من المبلغ 980JD 

للتحقق من صحة الحل $$\begin{gathered} 420+980 =1400 \mathrm{JD} \\ 1400\mathrm{JD}=1400\mathrm{JD} \end{gathered}$$

 

اشتركَ ثلاثةُ أشخاصٍ في شراءِ سيارةِ أجرةٍ بِمبلغِ 45000JD واتّفقوا على أنَّ نِسَبَ مُلكيةِ السيارةِ بينَهُمْ الأولُ إلى الثاني إلى الثالثِ بالشكلِ 3:4:2 ، وأنْ يدفعَ كلٌّ منهُمْ مِنْ ثَمَنِها حسبَ نسبةِ ملكيّتِهِ. أَجِدُ المبلغَ الّذي دفعَهُ كلٌّ منهُمْ، وأتحققُ مِنْ صحةِ الحلِّ.

 أَجِدُ مقدارَ الجزءِ الواحدِ مِنَ الربحِ.

$2+4+3=9$                 أَجِدُ عددَ الأجزاءِ جميعِها   

$\frac{45000}{9}=5000\mathrm{JD}$      أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

ولإيجادِ المبلغ الّذي سيحصلُ سيدفعه كلٌّ مِنْ الشركاء؛ أَضربُ النسبةَ الخاصةَ بكلٍّ منهُما في حصة الجزءِ الواحدِ:

$3\times 5000=15000\mathrm{JD}$             المبلغ الذي سيدفعه الشريك الأول  15000JD

$4\times 5000=20000\mathrm{JD}$            المبلغ الذي سيدفعه الشريك الثاني   20000JD

$2\times 5000=10000\mathrm{JD}$            المبلغ الذي سيدفعه الشريك الثالث  10000JD 

للتحقق من صحة الحل $$\begin{gathered} 15000+20000+10000=45000 \\ 45000=45000 \end{gathered}$$

 

تُوُفِّيَ رجلٌ وتركَ 30000JD لورثتِهِ وهم: ولدٌ، وثلاثُ بناتٍ، إذا أوصى بِسُدُسِ تَرِكَتِهِ للجمعياتِ الخيريةِ، فأحسبُ نصيبَ كلٍّ مِنَ الوَرَثةِ.

الْخُطْوَةُ 1: أجد النصيب الموصى به للجمعيات الخيرية 

$\frac{30000}{6}=5000 \mathrm{JD}$                       المبلغ الموصى به للجمعيات الخيرية 5000JD 

الْخُطْوَةُ 2:أَجِدُ ما تبقّى مِنَ التَّرِكَةِ بعد اخراج نصيب الجمعيات 

$30000-5000=25000\mathrm{JD}$          نطرح حصة الجمعيات من التركة 

الْخُطْوَةُ 3: أُوزّعُ ما تبقّى مِنَ التَّرِكَةِ على الولد و البنات الثلاثة بحيثُ تكونُ النِّسَبُ 2:1:1:1

$2+1+1+1=5$                            أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{25000}{5}=5000\mathrm{JD}$                      أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$2\times 5000=10000$                       أَجِدُ نصيب الولد بالضرب في 2 

نصيب كل بنت 5000JD ونصيب الولد 10000JD 

للتحقق من صحة الحل  $$\begin{gathered} 10000+3\times 5000+\left(5000\right)=30000 \mathrm{JD} \\ 30000=30000 \mathrm{JD} \end{gathered}$$

 

إذا كانَتْ نسبةُ المُذيبِ إلى المُذابِ في محلولٍ 3:2 وكانَتْ كمّيةُ المحلولِ 250mL ، أَجِدُ كمّيةَ كلٍّ مِنَ المُذيبِ وَالمُذابِ. 

$3+2=5$                                       أَجِدُ عددَ الأجزاءِ جميعِها      

$250÷5=50$                               أَجِدُ مقدارَ الجزءِ الواحدِ بالقسمةِ على 5        

$3\times 50=150\mathrm{mL}$                          أَجِدُ كمّيةَ المُذيبِ بالضربِ في عددِ أجزائِهِ

 $2\times 5=100\mathrm{mL}$                           أَجِدُ كمّيةَ المُذابِ بالضربِ في عددِ أجزائِهِ

للتحقق من صحة الحل $$\begin{gathered} 100+150=250\mathrm{mL} \\ 250\mathrm{mL}=250\mathrm{mL} \end{gathered}$$

---

---

اجابات أسئلة أتدرب وأحل المسائل

 

1) طعامٌ: وُزّعَ طَبَقُ بيتزا مكوّنٌ مِنْ 14 جزءًا متماثلً بينَ شخصَينِ بنسبةِ 3:4 أَجِدُ نصيبَ كلِّ واحدٍ منهُما.

$3+4=7$                                أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{14}{7}=2$                                 أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$2\times 3=6$                                نصيب الأول 6 أجزاء 

$2\times 4=8$                                نصيب الثاني 8 أجزاء 

 

2) حدائقُ: حديقةٌ مثلَّثةُ الشكلِ، النسبةُ بينَ أطوالِ أضلاعِها 3:4:5 ،فإذا كانَ محيطُها 120m، أحسبُ أطوالَ أضلاعِ هذهِ الحديقةِ.

$3+4+5=12$                    أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{120}{12}=10$                         أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 3\times 10=30\mathrm{cm} \\ 4\times 10=40\mathrm{cm} \\ 5\times 10=50\mathrm{cm} \end{gathered}$$                 أطوال الاضلاع بالترتيب 

 

3) معادنُ:معدِنٌ كُتلتُهُ 187g مكوَّنٌ مِنْ نحاسٍ وفضةٍ بنسبةِ$\frac{\mathbf{1}}{\mathbf{4}}\mathbf{:}\frac{\mathbf{1}}{\mathbf{7}}$ما كمّيةُ كلٍّ مِنَ النحاسِ والفضةِ في المعدِنِ؟

بالضرب في المضاعف المشترك الأصغر للعددين في المقام 28 لتكافئ النسبة 7:4 

$7+4=11$                     أَجِدُ عددَ الأجزاءِ جميعِها

$\frac{187}{11}=17$                    أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 17\times 7=119\mathrm{g} \\ 17\times 4=68\mathrm{g} \end{gathered}$$             كمّيةُ  النحاسِ 119g  والفضةِ 68g في هذا المعدِنِ

 

4) مشاريعُ صغيرةٌ: اشتركَتْ ثلاثُ سيّداتٍ في مشروعٍ بيتيٍّ لصناعةِ الصابونِ وبَيعِهِ،فدفعَتِ الأولى 500JD والثانيةُ 300JD والثالثةُ 400JD وفي نهايةِ العامِ كانَ ،صافي الأرباحِ 2400JD أَجِدُ نصيبَ كلِّ واحدةٍ منهُنَّ إذا وُزّعَتِ الأرباحُ حسبَ مساهمةِ كلٍّ منهُنَّ في رأسِ مالِ المشروعِ، وأتحققُ مِنْ صحةِ الحلِّ.

$\frac{500}{100}:\frac{300}{100}:\frac{400}{100}=5:3:4$                 أَجِدُ النسب بين الدفعات 

12=3+4+5                                              أَجِدُ عددَ الأجزاءِ جميعِها  

$\frac{2400\mathrm{JD}}{12}=200\mathrm{JD}$                            أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 5\times 200=1000\mathrm{JD} \\ 3\times 200=600\mathrm{JD} \\ 4\times 200=800\mathrm{JD} \end{gathered}$$                            نصيب الأولى 1000JD والثانية 600JD والثالثة 800JD 

للتحقق من صحة الحل $$\begin{gathered} 1000+600+800=2400\mathrm{JD} \\ 2400\mathrm{JD}=2400\mathrm{JD} \end{gathered}$$

5) قُسّمَ مبلغُ 2800JD بينَ عاملٍ وَفنّيٍّ وَمهندسٍ بنسبةِ $\frac{\mathbf{1}}{\mathbf{4}}\mathbf{:}\frac{\mathbf{1}}{\mathbf{2}}\mathbf{:}\mathbf{1}$ أَجِدُ نصيبَ كلِّ واحدٍ منهُمْ مِنَ المبلغِ.

$\frac{1}{4}+\frac{1}{2}+1=1.75$                       أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{2800}{1.75}=1600$                              أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 1600\times \frac{1}{4}=400\mathrm{JD} \\ 1600\times \frac{1}{2}=800\mathrm{JD} \\ 1600\times 1=1600\mathrm{JD} \end{gathered}$$                    نصيب العامل 400JD والفني 800JD والمهندس 1600JD 

 

6) ميراثٌ: تُوُفّيَتْ سيدةٌ، وتركَتْ لِوَرَثَتِها، وَهُمْ زوجٌ وولدٌ وبنتٌ، مبلغَ 18000JD أحسبُ نصيبَ كلٍّ مِنَ الوَرَثةِ علمًا أنَّ للزوجِ $\frac{\mathbf{1}}{\mathbf{4}}$التَّرِكَةِ، وَللولدِ مِثْلَيِ البنتِ.

نصيب الزوج    $\frac{18000}{4}=4500\mathrm{JD}$

$$\begin{gathered} 18000-4500=13500 \\ 2+1=3 \\ \frac{13500}{3}=4500 \end{gathered}$$                أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ بعد طرح نصيب الزوج من التركة 

الابن $4500\times 2=9000\mathrm{JD}$

البنت 4500JD 

 

7) قُطِّعَ أنبوبٌ بلاستيكيٌّ طولُهُ 1.2m إلى ثلاثةِ أجزاءٍ بنسبةِ 5:3:2 ، أَجِدُ طولَ كلِّ جزءٍ بالسّنتيمترِ.

$2+3+5=10$                             أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{120\mathrm{cm}}{10}=12\mathrm{cm}$                        أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 5\times 12=60\mathrm{cm} \\ 3\times 12=36\mathrm{cm} \\ 2\times 12=24\mathrm{cm} \end{gathered}$$                           الجزء الاول 60cm  و الثاني 36cm والثالث 24cm                      

 

8) هندسةٌ: مثلثٌ متطابقُ الضّلعَينِ، نسبةُ طولِ أحدِ الضّلعَينِ المتطابقَينِ إلى طولِ الضّلعِ الثالثِ هِيَ 2:3 إذا كانَ محيطُ المثلَّثِ 70cm أَجِدُ أطوالَ أضلاعِهِ.

$2+2+3=7$                             أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{70}{7}=10$                                  أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 2\times 10=20\mathrm{cm} \\ 2\times 10=20\mathrm{cm} \\ 3\times 10=30\mathrm{cm} \end{gathered}$$                        الضلع المتطابقين (الاول و الثاني) 20cm لكل منهما  والثالث 30cm         

 

9) طقسٌ: إذا كانَتْ نسبةُ عددِ الأيامِ العاصفةِ إلى عددِ الأيامِ المُشمِسةِ إلى عددِ الأيامِ الماطرةِ في شهرِ نَيسانَ هِيَ 3:2:5 أَجِدُ عددَ الأيامِ العاصفةِ، وَعددَ الأيامِ الماطرةِ.

$3+2+5=10$                         أَجِدُ عددَ الأجزاءِ جميعِها 

$\frac{30\mathrm{day}}{10}=3$                            أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 3\times 3=9 \mathrm{days} \\ 3\times 2=6 \mathrm{days} \\ 3\times 5= 15 \mathrm{days} \end{gathered}$$                   عدد الأيام العاصفة 9 أيام وعدد الأيام الماطرة 15 يوم 

 

10) إذا كانَتِ النسبةُ بينَ قياساتِ زوايا مثلَّثٍ 1:2:3 أَجِدُ قياساتِ زواياه.

$1+2+3=6$                         أَجِدُ عددَ الأجزاءِ جميعِها  

$\frac{{180}^{°}}{6}={30}^{\circ }$                        أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

$$\begin{gathered} 1\times {30}^{°}={30}^{°} \\ 2\times {30}^{°}={60}^{°} \\ 3\times {30}^{°}={90}^{°} \end{gathered}$$                       الزاوية الصغرى 30درجة والوسطى 60 درجة والكبرى 90 درجو 

 

11) أعودُ إلى فقرةِ (أستكشفُ)بدايةَ الدرسِ، وأحلُّ المسألةَ.

توزع الأرباح 1400دينار بالنسبة 2:4:1  نصيب حسن 400 وسعيد 800 وسليم 200 

 

أكتشفُ الخطأَ: خليطٌ مكوَّنٌ مِنْ ثلاثةِ ألوانٍ: الأحمرِ، والأزرقِ، والأبيضِ، بِنِسَبةِ 3:2:1 كمّيتُهُ 660mL لتحديدِ الكمّيةِ المستخدَمةِ مِنْ كلِّ لونٍ في الخليطِ،استخدمَ سليمٌ طريقتَينِ، وحصلَ على إجابةٍ خاطئةٍ في كلٍّ منهُما: 

الطريقة الأولى	الطريقة الثانية
3+2+1=6	الأحمر 220=660/3
660/6=110	الأزرق330 = 660/2
الأحمر 220 =110$\times$2	الأبيض 660=660/1
الازرق 110=110$\times$1
الأبيض330=110$\times$3

12) أوضّحُ الخطأَ الّذي وقعَ فيهِ سليمٌ في كلِّ طريقةٍ.

الطريقة الأولى : الخطأ أنه وزع حجم الخليط على الألوان بشكل غير صحيح.أعطيت نسبة الأحمر للأبيض، الأبيض للأزرق، الأزرق للأحمر.

الطريقة الثانية :الخطأ أنه قسم حجم الخليط على النسب مباشرة.يجب جمع الأجزاء أولا 

13) ما الإجابةُ الصحيحةُ؟

مجموع الأجزاء 6=1+2+3

الأحمر 330 الأزرق 220 والأبيض 110 

 

14) تحدٍّ: قطعةُ أرضٍ مستطيلةُ الشكلِ، نسبةُ طولِها إلى عَرضِها 5:3 فإذا كانَ محيطُها 160m ، أَجِدُ مساحتَها.

8=5+3                                    أَجِدُ عددَ الأجزاءِ جميعِها  

20=160/8                              أَجِدُ قيمةَ الجزءِ الواحدِ بالقسمةِ على عددِ الأجزاءِ

100=20$\times$5                           أجد الطول 

60=20$\times$3                             أجد العرض 

المساحة = الطول $\times$العرض  = 100 $\times$ 60 = 6000m²

 

15) تبريرٌ: أعدَّ رامي خليطًا مِنَ العصيرِ الطبيعيِّ يحتوي البرتقالَ والليمونَ والزَّنجبيلَ 40:9:1 وأعدَّتْ مَيْسُ خليطًا مِنَ المكوِّناتِ نفسِها ولكنْ بالنسبةِ 10:2:1 أيُّ الخليطَينِ فيهِ نسبةٌ أكبرُ مِنَ الزَّنجبيلِ؟ أبرّرُ إجابتي

نجمع الأجزاء لخليط رامي ونجد نسبة الزنجبيل فيها 50= 1+9+40 $\underset{}{\leftarrow }$ 1/50

نجمع الأجزاء لخليط ميس ونجد نسبة الزنجبيل فيها 13=1+2+10  $\underset{}{\leftarrow }$1/13

$\frac{1}{13}>\frac{1}{50}$ نسبة الزنجبيل في خليط ميس أكبر.

 

16) تحدٍّ: أقسمُ شبكةَ المربّعاتِ المجاورةَ إلى ثلاثةِ أجزاءٍ مستخدِمًا خطَّينِ، بحيثُ تكونُ النسبةُ بينَ المساحاتِ الناتج 2:3:4 

 

       أقسم الشبكة إلى 3 مناطق مستعملا التقسيم التناسبِيَّ.

       9=2+3+4  عدد الأجزاء 

       4 = 36/9    قيمة الجزء الواحد 

       الجزء الأول 8 مربعات الجزء الثاني 12 مربع والثالث 16 مربع 

 

17) أكتبُُ كيفَ أوظّفُ التقسيمَ التناسُبِيَّ في حلِّ مسائلَ حياتيةٍ؟

نستطيع توظيفه في مسائل حياتية  مثل: تقسيم الميراث، ورأس المال،ونسب المواد الداخلة في تكوين الأدوية والمحاليل.

---

---

اجابات أسئلة كتاب التمارين

1) يحتوي طعامٌ على خليطٍ مِنَ الشوفانِ وَالمكسَّراتِ وَرقائقِ القمحِ بِنسبةِ 3:2:1 إذا احتوَتْ عُبُوّةٌ على 720g مِنْ هذا الطعامِ، أَجِدُ كَمْ غرامًا مِنْ كلِّ نوعٍ في هذِهِ العُبُوّةِ.

$$\begin{gathered} 3+2+1=6 \\ \frac{720}{6}=120 \end{gathered}$$

الشوفانِ $120\times 3=360\mathrm{g}$          

المكسَّراتِ $120\times 2=240\mathrm{g}$

رقائقِ القمحِ $120\times 1=120\mathrm{g}$

 

2) اشتركَ ثلاثةُ أشخاصٍ في تجارةٍ، فَدفعَ الأولُ 5000JD وَدفعَ الثاني 8000JD وَدفعَ الثالثُ 7000JD ثمَّ اتفقوا على أَنْ يأخذَ الأولُ $\frac{\mathbf{1}}{\mathbf{7}}$الأرباحِ بَدلَ إدارتِهِ التجارةَ، وَتوزَّعُ باقي الأرباحِ حسبَ مساهمةِ كلٍّ مِنْهُمْ في رأسِ المالِ. إذا كانَ صافي أرباحِ تجارتِهِمْ نِهايةَ العامِ 4900JD أَجِدُ نصيبَ كلٍّ مِنْهُمْ.

$$\begin{gathered} \frac{4900}{7}=700 \\ 4900-700=4200 \end{gathered}$$

$$\begin{gathered} 5+8+7=20 \\ \frac{4200}{20}=210 \end{gathered}$$

الاول $210\mathrm{JD}\times 5+700\mathrm{JD}=1750\mathrm{JD}$

الثا ني $210\mathrm{JD}\times 8=1680\mathrm{JD}$

الثالث $210\mathrm{JD}\times 7=1470\mathrm{JD}$

 

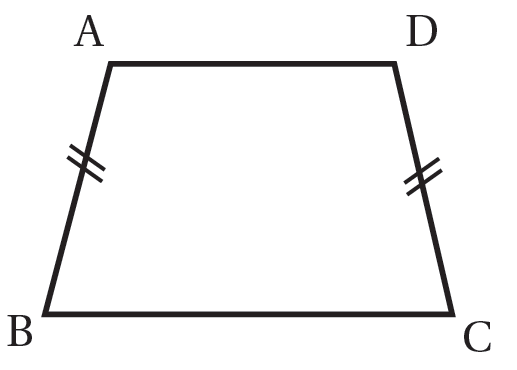
3) في الشكلِ المجاورِ شبهُ منحرفٍ متساوي الساقَينِ، إذا كانَتْ نسبةُ طولِ $\overline{\mathrm{AD}}$ إِلى طولِ $\overline{\mathrm{AB}}$ إِلى طولِ $\overline{\mathrm{BC}}$  هِيَ 2:3:4 وَكانَ محيطُهُ 60cm أَجِدُ طولَ كلِّ ضلعٍ مِنْ أضلاعِهِ .

$\overline{\mathrm{AB}}=\overline{\mathrm{DC}}$

$$\begin{gathered} 2+3+3+4=12 \\ 60÷12=5 \\ \overline{\mathrm{AD}} \underset{}{\to }2\times 5=10 \\ \underset{}{\overline{\mathrm{DC}}\to }3\times 5=15 \\ \underset{}{\overline{\mathrm{AB}}\to }3\times 5=15 \\ \underset{}{\overline{\mathrm{BC}}\to }4\times 5=20 \end{gathered}$$ 

 

4) قُسِّمَتْ قطعةُ أرضٍ بينَ شريكَينِ بِنسبةِ 4:7 إذا كانَ نصيبُ الثاني يزيدُ 300m² عَنْ نصيبِ الأولِ، أَجِدُ مساحةَ قطعةِ الأرضِ وَنصيبَ الأولِ وَالثاني.

$$\begin{gathered} 7+4=11 \\ 7\times \frac{\mathrm{X}}{11}=4\times \frac{\mathrm{X}}{11}+300 \\ \mathrm{X}=1100{\mathrm{m}}^2 \end{gathered}$$

المساحة الكلية للارض    1100m²

نصيب الأول                    $\frac{1100}{11}\times 4=400{\mathrm{m}}^2$

نصيب الثاني                    $400+300=700{\mathrm{m}}^2$                  

 

5) تُوُفّيَتْ سيدةٌ عَنْ أبٍ وَزوجٍ وَولدٍ وَبنتٍ، وَتركَتْ مبلغَ 18000JD إذا علمْتُ أَنَّ قسمَةَ الميراثِ: السُّدُسُ لِلأبِ،وَالرُّبُعُ لِلزوجِ، وَللولدِ مِثْلَيِ البنتِ، فَأَجِدُ نصيبَ كلِّ وريثٍ لِلسيدةِ.

الأب     $\frac{18000}{6}=3000\mathrm{JD}$

الزوج    $\frac{18000}{4}=4500\mathrm{JD}$

$$\begin{gathered} 18000-\left(3000+4500\right)=10500 \\ 2+1=3 \\ \frac{10500}{3}=3500 \end{gathered}$$

الإبن      $2\times 3500=7000\mathrm{JD}$

البنت     3500JD

 

6) يريدُ منذرٌ وَماجدةُ تقسيمَ 12870JD بينَهُما بنسبةِ 3:2 . يقولُ منذرٌ: سوفَ أحصلُ على 4290JD وَسَتحصلُ ماجدةُ على 6435JD  $\mathbf{12870}\mathbf{÷}\mathbf{3}\mathbf{=}\mathbf{4290}\mathbf{JD}$ و $\mathbf{12870}\mathbf{÷}\mathbf{=}\mathbf{6435}\mathbf{JD}$  هلْ ما يقولُهُ منذرٌ صحيحٌ؟ أبرّرُ إجابتي

 .( غير صحيح لأن القسمة تتم على مجموع الأجزاء أولا ( 5

قيمة الجزء الواحد 2574JD

نصيب منذر 7722JD

نصيب ماجدة 5148JD

 

7) كيفَ أتحققُ مِنْ صحةِ إجابتي عَنْ سؤالٍ يتطلّبُ تقسيمَ مبلغٍ مِنَ المالِ بينَ شركاءَ بِنسبةٍ معطاةٍ؟

أجد مجموع ما أخذوه جميعا، يجب أم يطابق هذا المجموع المبلغ الذي تم توزيعه