رياضيات فصل ثاني

التوجيهي علمي

الشرح الملخص أوراق العمل حل اسئلة الدرس النتاجات

التكامل بالتعويض الدرس الثاني :

أجد كلاً من التكاملات الآتية :

أتحقق من فهمي صفحة 32 .

$a \int 4 x^{2} \sqrt{x^{3} - 5} d x S o l u t i o n : l e t u = x^{3} - 5 \Rightarrow d x = \frac{d u}{3 x^{2}} \int 4 x^{2} \sqrt{x^{3} - 5} d x = \int 4 x^{2} u^{\frac{1}{2}} \frac{d u}{3 x^{2}} = \frac{4}{3} \int x^{2} u^{\frac{1}{2}} \frac{d u}{x^{2}} = \frac{4}{3} \int u^{\frac{1}{2}} d u = \frac{4}{3} \times \frac{2}{3} u^{\frac{3}{2}} = \frac{8}{9} {(x^{3} - 5)}^{\frac{3}{2}} + c$

$b \int \frac{1}{2 \sqrt{x}} e^{\sqrt{x}} d x S o l u t i o n : l e t u = \sqrt{x} \Rightarrow d x = \frac{d u}{\frac{1}{2 \sqrt{x}}} = 2 \sqrt{x} d u \int \frac{1}{2 \sqrt{x}} e^{\sqrt{x}} d x = \int \frac{1}{2 \sqrt{x}} e^{u} \times 2 \sqrt{x} d u = \int \frac{1}{2 \sqrt{x}} e^{u} \times 2 \sqrt{x} d u = \int e^{u} d u = e^{u} = e^{\sqrt{x}} + c$

$c \int \frac{{(l n x)}^{3}}{x} d x S o l u t i o n : l e t u = l n x \Rightarrow d x = \frac{d u}{\frac{1}{x}} = x d u \int \frac{{(l n x)}^{3}}{x} d x = \int \frac{u^{3}}{x} x d u = \int \frac{u^{3}}{x} x d u = \int u^{3} d u = \frac{u^{4}}{4} = \frac{1}{4} {(l n x)}^{4} + c$

$d \int \frac{c o s (l n x)}{x} d x S o l u t i o n : l e t u = l n x \Rightarrow d x = \frac{d u}{\frac{1}{x}} = x d u \int \frac{c o s (l n x)}{x} d x = \int \frac{c o s u}{x} x d u = \int \frac{c o s u}{x} x d u = \int c o s u d u = s i n u = s i n (l n x) + c$

$e \int c o s^{4} 5 x s i n 5 x d x S o l u t i o n : l e t u = c o s 5 x \Rightarrow d x = \frac{d u}{- 5 s i n 5 x} \int c o s^{4} 5 x s i n 5 x d x = \int u^{4} s i n 5 x \frac{d u}{- 5 s i n 5 x} = - \frac{1}{5} \int u^{4} s i n 5 x \frac{d u}{s i n 5 x} = - \frac{1}{5} \int u^{4} d u = - \frac{1}{25} u^{5} = - \frac{1}{25} {(c o s 5 x)}^{5} + c$

$f \int x 2^{x^{2}} d x S o l u t i o n : l e t u = x^{2} \Rightarrow d x = \frac{d u}{2 x} \int x 2^{x^{2}} d x = \int x 2^{u} \frac{d u}{2 x} = \frac{1}{2} \int x 2^{u} \frac{d u}{x} = \frac{1}{2} \int 2^{u} d u = \frac{2^{u}}{l n 2} = \frac{2^{x^{2}}}{l n 2} + c$

أتحقق من فهمي صفحة 34 .

أجد كلاً من التكاملات الآتية :

$a \int \frac{x}{\sqrt{1 + 2 x}} d x S o l u t i o n : l e t u = \sqrt{2 x + 1} \Rightarrow d x = \frac{d u}{\frac{2}{2 \sqrt{2 x + 1}}} = \sqrt{2 x + 1} d u = u d u \Rightarrow d x = u d u b u t x = \frac{u^{2} - 1}{2} \int \frac{x}{\sqrt{2 x + 1}} d x = \int \frac{x}{u} u d u = \int \frac{x}{u} u d u = \int x d u = = \int \frac{u^{2} - 1}{2} d u = \frac{1}{2} (\frac{1}{3} u^{3} - u) = \frac{1}{6} {(\sqrt{2 x + 1})}^{3} - \sqrt{2 x + 1} + c$ ملاحظة : يمكن حل هذا السؤال (لاحقاً) بالأجزاء

$b \int x^{7} {(x^{4} - 8)}^{3} d x S o l u t i o n : l e t u = x^{4} - 8 \Rightarrow d x = \frac{d u}{4 x^{3}} b u t x^{4} = u - 8 \int x^{7} {(x^{4} - 8)}^{3} d x = \int x^{7} u^{3} \frac{d u}{4 x^{3}} = \frac{1}{4} \int {\overset{x^{4}}{x^{7}} u}^{3} \frac{d u}{x^{3}} = \int x^{4} u^{3} d u b u t x^{4} = u - 8 = \int (u - 8) u^{3} d u = \int (u^{4} - 8 u^{3}) d u = \frac{1}{5} u^{5} - \frac{8}{4} u^{4} = \frac{1}{5} {(x^{4} - 8)}^{5} - \frac{8}{4} {(x^{4} - 8)}^{4} + c$

$c \int \frac{e^{3 x}}{{(1 - e^{x})}^{2}} d x S o l u t i o n : l e t u = 1 - e^{x} \Rightarrow d x = \frac{d u}{- e^{x}} b u t e^{x} = 1 - u \int \frac{e^{3 x}}{{(1 - e^{x})}^{2}} d x = \int \frac{e^{3 x}}{u^{2}} \frac{d u}{- e^{x}} = - \int \frac{{(e^{x})}^{2}}{u^{2}} d u b u t e^{x} = 1 - u = - \int \frac{{(1 - u)}^{2}}{u^{2}} d u = - \int \frac{1 - 2 u + u^{2}}{u^{2}} d u = \int (u^{- 2} - \frac{2}{u} + 1) d u = - \frac{1}{u} - 2 l n u + u = - \frac{1}{1 - e^{x}} - 2 l n (1 - e^{x}) + 1 - e^{x} + c$

أتحقق من فهمي صفحة 35 .

أجد كلاً من التكاملات الآتية :

$a \int \frac{1}{x + \sqrt[3]{x}} d x S o l u t i o n : l e t u = x^{\frac{1}{3}} \Rightarrow u^{3} = x \Rightarrow 3 u^{2} d u = d x b u t x = u^{3} \int \frac{1}{x + x^{\frac{1}{3}}} d x = \int \frac{1}{u^{3} + u} 3 x^{\frac{2}{3}} d u = 3 \int \frac{u^{2}}{u^{3} + u} d u = \frac{3}{2} \int \frac{2 u}{u^{2} + 1} d u = \frac{3}{2} l n (u^{2} + 1) = \frac{3}{2} l n (x^{\frac{2}{3}} + 1) + c T h e f a s t s o l u t i o n : \int \frac{1}{x + x^{\frac{1}{3}}} d x = \int \frac{x^{\frac{- 1}{3}}}{x^{\frac{- 1}{3}} (x + x^{\frac{1}{3}})} d x = \frac{3}{2} \int \frac{\frac{2}{3} x^{\frac{- 1}{3}}}{x^{\frac{2}{3}} + 1} d x = \frac{3}{2} l n (x^{\frac{2}{3}} + 1) + c$

$b \int x \sqrt[3]{{(1 - x)}^{2}} d x S o l u t i o n : l e t u = {(1 - x)}^{\frac{2}{3}} \Rightarrow d x = \frac{d u}{\frac{2}{3} {(1 - x)}^{\frac{- 1}{3}}} = \frac{3}{2} {(1 - x)}^{\frac{1}{3}} d u b u t 1 - x = u^{\frac{3}{2}} \Rightarrow x = 1 - u^{\frac{3}{2}} \int x \sqrt[3]{{(1 - x)}^{2}} d x = \int x u \times \frac{3}{2} {(1 - x)}^{\frac{1}{3}} d u = \frac{3}{2} \int (1 - u^{\frac{3}{2}}) u \times {(u^{\frac{3}{2}})}^{\frac{1}{3}} d u = \frac{3}{2} \int (1 - u^{\frac{3}{2}}) u^{\frac{3}{2}} d u = \frac{3}{2} \int (u^{\frac{3}{2}} - u^{3}) d u = \frac{3}{2} (\frac{2}{5} u^{\frac{5}{2}} - \frac{1}{4} u^{4}) = \frac{3}{5} u^{\frac{5}{2}} - \frac{3}{8} u^{4} = \frac{3}{5} {(1 - x)}^{\frac{10}{6}} - \frac{3}{8} {(1 - x)}^{\frac{8}{3}} + c$

أتحقق من فهمي صفحة 37 .

يُمثل الاقتران p(x) ، سعر القطعة بالدينار ، تستعمل في أجهزة الحاسوب ، حيث x عدد القطع المبيعة بالمئات .

إذا كان $p' (x) = \frac{- 135 x}{\sqrt{9 + x^{2}}}$ هو معدل تغيّر سعر هذه القطعة ، فأجد p(x) . علماً بأن سعر القطعة الواحدة

هو 30 JD عندما يكون عدد القطع المعيبة منها 400 قطعة .

$S o l u t i o n : p' (x) = \frac{- 135 x}{\sqrt{9 + x^{2}}} \Rightarrow p (x) = \int \frac{- 135 x}{\sqrt{9 + x^{2}}} d x l e t u = 9 + x^{2} \Rightarrow d x = \frac{d u}{2 x} \int \frac{- 135 x}{\sqrt{9 + x^{2}}} d x = \int \frac{- 135 x}{\sqrt{u}} \frac{d u}{2 x} = \frac{- 135}{2} \int \frac{x}{\sqrt{u}} \frac{d u}{x} = \frac{- 135}{2} \int u^{- \frac{1}{2}} d u = - 135 u^{\frac{1}{2}} p (x) = - 135 {(9 + x^{2})}^{\frac{1}{2}} + c p (400) = - 135 {(9 + {(400)}^{2})}^{\frac{1}{2}} + c = 30 \Rightarrow c = 30 + 135 \sqrt{(9 + {(400)}^{2})} \approx 54031.5 \Rightarrow p (x) = - 135 \sqrt{9 + x^{2}} + 54031.5$

أتحقق من فهمي صفحة 39 .

أجد كلاً من التكاملات الآتية :

$a \int s i n^{3} x d x S o l u t i o n : l e t s i n^{3} x = s i n^{2} x \times s i n x = (1 - c o s^{2} x) s i n x l e t u = c o s x \Rightarrow d x = \frac{d u}{- s i n x} \int s i n^{3} x d x = \int (1 - c o s^{2} x) s i n x d x = \int (1 - u^{2}) s i n x \frac{d u}{- s i n x} = \int (1 - u^{2}) s i n x \frac{d u}{- s i n x} = - \int (1 - u^{2}) d u = - u + \frac{1}{3} u^{3} = - c o s x + \frac{1}{3} c o s^{3} x + c$

$b \int c o s^{5} x s i n^{2} x d x S o l u t i o n : l e t c o s^{5} x = c o s^{3} x \times c o s^{2} x = c o s^{3} x \times (1 - s i n^{2} x) l e t u = s i n x \Rightarrow d x = \frac{d u}{c o s x} \int c o s^{5} x s i n^{2} x d x = \int c o s^{3} x (1 - s i n^{2} x) s i n^{2} x d x = \int c o s^{3} x (1 - u^{2}) u^{2} \frac{d u}{c o s x} = \int c o s^{2} x (1 - u^{2}) u^{2} d u = \int (1 - u^{2}) (1 - u^{2}) u^{2} d u = \int (1 - 2 u^{2} + u^{4}) u^{2} d u = \int (u^{2} - 2 u^{4} + u^{6}) d u = \frac{1}{3} u^{3} - \frac{2}{5} u^{5} + \frac{1}{7} u^{7} = \frac{1}{3} s i n^{3} x - \frac{2}{5} s i n^{5} x + \frac{1}{7} s i n^{7} x + c$

أتحقق من فهمي صفحة 41 .

أجد كلاً من التكاملات الآتية :

$a \int t a n^{4} x d x S o l u t i o n : l e t t a n^{4} x = t a n^{2} x \times t a n^{2} x = (s e c^{2} x - 1) t a n^{2} x = t a n^{2} x s e c^{2} x - t a n^{2} x l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int t a n^{4} x d x = \int (t a n^{2} x s e c^{2} x - t a n^{2} x) d x = \int (t a n^{2} x s e c^{2} x) d x - \int (t a n^{2} x) d x = \int (t a n^{2} x s e c^{2} x) d x - \int (s e c^{2} x - 1) d x = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} - t a n x + x = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} - t a n x + x = \int u^{2} d u - t a n x + x = \frac{1}{3} u^{3} - t a n x + x = \frac{1}{3} t a n^{3} x - t a n x + x + c$

$b \int c o t^{5} x d x S o l u t i o n : l e t c o t^{5} x = c o t^{2} x \times c o t^{3} x = (c s c^{2} x - 1) c o t^{3} x = c o t^{3} x c s c^{2} x - c o t^{2} x \times c o t x = c o t^{3} x c s c^{2} x - (c s c^{2} x - 1) \times c o t x = c o t^{3} x c s c^{2} x - c o t x c s c^{2} x - c o t x l e t u = c o t x \Rightarrow d x = - \frac{d u}{c s c^{2} x} \int c o t^{5} x d x = \int (c o t^{3} x c s c^{2} x - c o t x c s c^{2} x) d x - \int c o t x d x = - \int u^{3} x c s c^{2} x \frac{d u}{c s c^{2} x} + \int u c s c^{2} x \frac{d u}{c s c^{2} x} - \int \frac{c o s x}{s i n x} d x = - \int u^{3} x c s c^{2} x \frac{d u}{c s c^{2} x} + \int u c s c^{2} x \frac{d u}{c s c^{2} x} - l n (s i n x) = - \int u^{3} d u + \int u d u - l n (s i n x) = - \frac{1}{4} u^{4} + \frac{1}{2} u^{2} - l n (s i n x) = - \frac{1}{4} c o t^{4} x + \frac{1}{2} c o t^{2} x - l n (s i n x) + c$

$c \int s e c^{4} x t a n^{6} x d x S o l u t i o n : l e t s e c^{4} x t a n^{6} x = s e c^{2} x s e c^{2} x t a n^{6} x = s e c^{2} x (t a n^{2} x + 1) t a n^{6} x = s e c^{2} x t a n^{8} x + s e c^{2} x t a n^{6} x l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int s e c^{4} x t a n^{6} x d x = \int (s e c^{2} x u^{8}) \frac{d u}{s e c^{2} x} - \int (s e c^{2} x u^{6}) \frac{d u}{s e c^{2} x} = \int (s e c^{2} x u^{8}) \frac{d u}{s e c^{2} x} - \int (s e c^{2} x u^{6}) \frac{d u}{s e c^{2} x} = \int u^{8} d u - \int u^{6} d u = \frac{1}{9} u^{9} + \frac{1}{7} u^{7} = \frac{1}{9} t a n^{9} x + \frac{1}{7} t a n^{7} x + c$

أتحقق من فهمي صفحة 43.

أجد كلاً من التكاملات الآتية :

$a \int_{0}^{2} x {(x + 1)}^{3} d x S o l u t i o n : l e t u = x + 1 \Rightarrow d x = d u x = u - 1 \int x {(x + 1)}^{3} d x = \int x u^{3} d u = \int (u - 1) u^{3} d u = \int (u^{4} - u^{3}) d u = \frac{1}{5} u^{5} - \frac{1}{4} u^{4} = \frac{1}{5} {(x + 1)}^{5} - \frac{1}{4} {(x + 1)}^{4} 2 0 = \frac{1}{5} ({(3)}^{5} - {(1)}^{5}) - \frac{1}{4} ({(3)}^{4} - {(1)}^{4}) = \frac{242}{5} - 20 = \frac{162}{5}$

$b \int_{0}^{\frac{π}{3}} t a n x s e c x \sqrt{s e c x + 2} d x S o l u t i o n : l e t u = s e c x + 2 \Rightarrow d x = \frac{d u}{s e c x t a n x} \int t a n x s e c x \sqrt{s e c x + 2} d x = \int t a n x s e c x u^{\frac{1}{2}} \frac{d u}{s e c x t a n x} = \int t a n x s e c x u^{\frac{1}{2}} \frac{d u}{s e c x t a n x} = \int u^{\frac{1}{2}} d u = \frac{2}{3} u^{\frac{3}{2}} = \frac{2}{3} {(s e c x + 2)}^{\frac{3}{2}} \frac{π}{3} 0 = \frac{2}{3} {(4)}^{\frac{3}{2}} - \frac{2}{3} {(3)}^{\frac{3}{2}} = \frac{16}{3} - 2 \sqrt{3}$

أتدرب وأحل المسائل .

أجد كلاً من التكاملات الآتية :

$1 \int x^{2} {(2 x^{3} + 5)}^{4} d x S o l u t i o n : l e t u = 2 x^{3} + 5 \Rightarrow d x = \frac{d u}{6 x^{2}} \int x^{2} {(2 x^{3} + 5)}^{4} d x = \int x^{2} u^{4} \frac{d u}{6 x^{2}} = \frac{1}{6} \int x^{2} u^{4} \frac{d u}{x^{2}} = \frac{1}{6} \int u^{4} d u = \frac{1}{30} u^{5} = \frac{1}{30} {(2 x^{3} + 5)}^{5} + c$

$2 \int x^{2} \sqrt{x + 3} d x S o l u t i o n : l e t u = x + 3 \Rightarrow d x = d u b u t x = u - 3 x^{2} = u^{2} - 6 u + 9 \int x^{2} \sqrt{x + 3} d x = \int x^{2} u^{\frac{1}{2}} d x = \int (u^{2} - 6 u + 9) u^{\frac{1}{2}} d x = \int (u^{\frac{5}{2}} - 6 u^{\frac{3}{2}} + 9 u^{\frac{1}{2}}) d u = \frac{2}{7} u^{\frac{5}{2}} - \frac{12}{5} u^{\frac{3}{2}} + 6 u^{\frac{1}{2}} = \frac{2}{7} {(x + 3)}^{\frac{5}{2}} - \frac{12}{5} {(x + 3)}^{\frac{3}{2}} + 6 {(x + 3)}^{\frac{1}{2}} + c$

$3 \int x {(x + 2)}^{3} d x S o l u t i o n : l e t u = x + 2 \Rightarrow d x = d u b u t x = u - 2 \int x {(x + 2)}^{3} d x = \int x u^{3} d u = \int (u - 2) u^{3} d u = \int (u^{4} - 2 u^{3}) d u = \frac{1}{5} u^{5} - \frac{2}{4} u^{4} = \frac{1}{5} {(x + 2)}^{5} - \frac{1}{2} {(x + 2)}^{4} + c$

$4 \int \frac{x}{\sqrt{x + 4}} d x S o l u t i o n : l e t u = x + 4 \Rightarrow d x = d u b u t x = u - 4 \int \frac{x}{\sqrt{x + 4}} d x = \int x u^{- \frac{1}{2}} d u = \int (u - 4) u^{- \frac{1}{2}} d u = \int (u^{\frac{1}{2}} - 4 u^{^{- \frac{1}{2}}}) d u = \frac{2}{3} u^{\frac{3}{2}} - 8 u^{\frac{1}{2}} = \frac{2}{3} {(x + 4)}^{\frac{3}{2}} - 8 {(x + 4)}^{\frac{1}{2}} + c$

$5 \int e^{s i n x} c o s x d x S o l u t i o n : l e t u = s i n x \Rightarrow d x = \frac{d u}{c o s x} \int e^{s i n x} c o s x d x = \int e^{u} \cos x \frac{d u}{\cos x} = \int e^{u} \cos x \frac{d u}{\cos x} = \int e^{u} d u = e^{u} + c = e^{s i n x} + c$

$6 \int \frac{e^{3 x}}{1 + e^{x}} d x S o l u t i o n : l e t u = 1 + e^{x} \Rightarrow d x = \frac{d u}{e^{x}} b u t e^{x} = u - 1 \int \frac{e^{3 x}}{1 + e^{x}} d x = \int \frac{e^{3 x}}{u} \frac{d u}{e^{x}} = \int \frac{{(e^{x})}^{3}}{u} d u b u t e^{x} = u - 1 = \int \frac{{(u - 1)}^{3}}{u} d u = \int \frac{u^{3} - 3 u^{2} + 3 u - 1}{u} d u = \int (u^{2} - 3 u + 3 - \frac{1}{u}) d u = \frac{1}{3} u^{3} - \frac{3}{2} u^{2} + 3 u - l n u = \frac{1}{3} {(1 + e^{x})}^{3} - \frac{3}{2} {(1 + e^{x})}^{2} - l n (1 + e^{x}) + 3 e^{x} + 3 + c$

$7 \int s e c^{4} x d x S o l u t i o n : l e t s e c^{4} x = s e c^{2} x \times s e c^{2} x = (t a n^{2} x + 1) s e c^{2} x = t a n^{2} x s e c^{2} x + s e c^{2} x l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int s e c^{4} x d x = \int (t a n^{2} x s e c^{2} x + s e c^{2} x) d x = \int (t a n^{2} x s e c^{2} x) d x + \int (s e c^{2} x) d x = \int (t a n^{2} x s e c^{2} x) d x + t a n x = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} + t a n x = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} + t a n x = \int u^{2} d u + t a n x = \frac{1}{3} u^{3} + t a n x = \frac{1}{3} s e c^{3} x + t a n x + c$

$8 \int \frac{t a n x}{c o s^{2} x} d x S o l u t i o n : l e t \frac{1}{c o s^{2} x} = s e c^{2} x \int t a n x s e c^{2} x d x = l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int s e c^{4} x d x = \int (t a n x s e c^{2} x) d x = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} = \int (u^{2} s e c^{2} x) \frac{d u}{s e c^{2} x} = \int u^{2} d u = \frac{1}{3} u^{3} = \frac{1}{3} s e c^{3} x + c$

$9 \int \frac{s i n (l n x)}{x} d x S o l u t i o n : l e t u = l n x \Rightarrow d x = \frac{d u}{\frac{1}{x}} \Rightarrow d x = x d u \int \frac{s i n (l n x)}{x} d x = \int \frac{s i n u}{x} x d u = \int \frac{s i n u}{x} x d u = \int s i n u d u = - c o s u = - c o s (l n x) + c$

$10 \int \sin 2 x {(4 + \sin^{2} x)}^{3} d x S o l u t i o n : l e t u = \sin^{2} x \Rightarrow d x = \frac{d u}{2 \sin x \cos x} = \frac{d u}{\sin 2 x} \int s i n 2 x {(4 + s i n^{2} x)}^{3} d x = \int \sin 2 x u^{3} \frac{d u}{\sin 2 x} = \int \sin 2 x u^{3} \frac{d u}{\sin 2 x} = u^{3} d u = \frac{u^{4}}{4} + c = \frac{\sin^{8} x}{4} + c$

$11 \int \frac{2 e^{x} - 2 e^{- x}}{{(e^{x} + e^{- x})}^{2}} d x S o l u t i o n : l e t u = e^{x} + e^{- x} \Rightarrow d x = \frac{d u}{e^{x} - e^{- x}} \int \frac{2 e^{x} - 2 e^{- x}}{{(e^{x} + e^{- x})}^{2}} d x = 2 \int \frac{e^{x} - e^{- x}}{u^{2}} \frac{d u}{e^{x} - e^{- x}} = 2 \int \frac{e^{x} - e^{- x}}{u^{2}} \frac{d u}{e^{x} - e^{- x}} = 2 \int u^{- 2} d u = - \frac{2}{u} = - \frac{2}{e^{x} + e^{- x}} + c$

$12 \int \frac{- x}{(x + 1) \sqrt{x + 1}} d x S o l u t i o n : \int \frac{- x}{(x + 1) \sqrt{x + 1}} d x = - \int x {(x + 1)}^{\frac{3}{2}} d x l e t u = x + 1 \Rightarrow d x = d u a n d x = u - 1 \int x {(x + 1)}^{\frac{3}{2}} d x = \int x u^{\frac{3}{2}} d u = \int (u - 1) u^{\frac{3}{2}} d u = \int (u^{\frac{5}{2}} - u^{^{\frac{3}{2}}}) d u = \frac{2}{7} u^{\frac{7}{2}} - \frac{2}{5} u^{\frac{5}{2}} = - \frac{2}{7} (x + 1)^{\frac{7}{2}} + \frac{2}{5} {(x + 1)}^{\frac{5}{2}} + c$

$13 \int x^{2} \sqrt[3]{x + 10} d x S o l u t i o n : l e t u = x + 10 \Rightarrow d x = d u b u t x = u - 10 x^{2} = u^{2} - 20 u + 100 \int x^{2} \sqrt[3]{x + 10} d x = \int x^{2} u^{\frac{1}{3}} d u = \int (u^{2} - 20 u + 100) u^{\frac{1}{3}} d u = \int (u^{\frac{7}{3}} - 20 u^{\frac{4}{3}} + 100 u^{\frac{1}{3}}) d u = \frac{3}{10} u^{\frac{10}{3}} - \frac{60}{7} u^{\frac{7}{3}} + 75 u^{\frac{4}{3}} = \frac{3}{10} {(x + 10)}^{\frac{10}{3}} - \frac{60}{7} {(x + 10)}^{\frac{7}{3}} + 75 {(x + 10)}^{\frac{4}{3}} + c$

$14 \int s e c^{2} \frac{x}{2} t a n^{7} \frac{x}{2} d x S o l u t i o n : l e t u = t a n \frac{x}{2} \Rightarrow d x = 2 \frac{d u}{s e c^{2} \frac{x}{2}} \int s e c^{2} \frac{x}{2} t a n^{7} \frac{x}{2} d x = 2 \int s e c^{2} \frac{x}{2} u^{7} \frac{d u}{s e c^{2} \frac{x}{2}} = 2 \int s e c^{2} \frac{x}{2} u^{7} \frac{d u}{s e c^{2} \frac{x}{2}} = 2 \int u^{7} d u = \frac{1}{4} u^{8} = \frac{1}{4} t a n^{8} x + c$

$15 \int \frac{s e c^{3} x + e^{s i n x}}{s e c x} d x S o l u t i o n : \int \frac{s e c^{3} x + e^{s i n x}}{s e c x} d x = \int s e c^{2} x d x + \int c o s x e^{s i n x} d x I_{1} = \int s e c^{2} x d x = t a n x I_{2} = \int c o s x e^{s i n x} d x l e t u = s i n x \Rightarrow d x = \frac{d u}{c o s x} \int c o s x e^{s i n x} d x = \int c o s x e^{u} \frac{d u}{c o s x} = \int c o s x e^{u} \frac{d u}{c o s x} = \int e^{u} d u = e^{u} = e^{s i n x} \int \frac{s e c^{3} x + e^{s i n x}}{s e c x} d x = I_{1} + I_{2} = t a n x + e^{s i n x} + c$

$16 \int (1 + \sqrt[3]{s i n x}) c o s^{3} x d x S o l u t i o n : c o s^{3} x = c o s x . c o s^{2} x b u t c o s^{2} x = 1 - s i n^{2} x \int (1 + \sqrt[3]{s i n x}) c o s^{3} x d x = \int c o s x (1 + \sqrt[3]{s i n x}) (1 - s i n^{2} x) d x l e t u = s i n x \Rightarrow d x = \frac{d u}{c o s x} \int c o s x (1 + \sqrt[3]{s i n x}) (1 - s i n^{2} x) d x = \int c o s x (1 + u^{\frac{1}{3}}) (1 - u^{2}) \frac{d u}{c o s x} = \int c o s x (1 + u^{\frac{1}{3}}) (1 - u^{2}) \frac{d u}{c o s x} = \int (1 + u^{\frac{1}{3}}) (1 - u^{2}) d u = \int (1 + u^{\frac{1}{3}} - u^{2} - u^{\frac{7}{3}}) d u = u + \frac{3}{4} u^{\frac{4}{3}} - \frac{u^{3}}{3} - \frac{3}{10} u^{\frac{10}{3}} = s i n x + \frac{3}{4} {(s i n x)}^{\frac{4}{3}} - \frac{s i n^{3} x}{3} - \frac{3 {(s i n x)}^{\frac{10}{3}}}{10} + c$

$17 \int s i n x s e c^{5} x d x S o l u t i o n : \int s i n x s e c^{5} x d x = \int \frac{s i n x}{c o s^{5} x} d x l e t u = \cos x \Rightarrow d x = - \frac{d u}{\sin x} \int \frac{s i n x}{c o s^{5} x} d x = \int \frac{s i n x}{u^{5}} \times - \frac{d u}{\sin x} = \int \frac{\sin x}{u^{5}} \times - \frac{d u}{\sin x} = - \int \frac{d u}{u^{5}} = \frac{1}{4 u^{4}} = \frac{1}{4 \cos^{4} x} + c$

$18 \int \frac{s i n x + t a n x}{c o s^{3} x} d x S o l u t i o n : b u t s i n x = \frac{t a n x}{s e c x}, a n d s e c x = \frac{1}{c o s x} \int \frac{s i n x + t a n x}{c o s^{3} x} d x = \int s e c^{3} x (\frac{t a n x}{s e c x} + t a n x) d x = \int (s e c^{2} x t a n x + s e c^{3} x t a n x) d x = \int (s e c x t a n x) (s e c x + s e c^{2} x) d x l e t u = s e c x \Rightarrow d x = \frac{d u}{s e c x t a n x} = \int (s e c x t a n x) (u + u^{2}) \frac{d u}{s e c x t a n x} = \int (s e c x t a n x) (u + u^{2}) \frac{d u}{s e c x t a n x} = \int (u + u^{2}) d u = \frac{u^{2}}{2} + \frac{u^{3}}{3} = \frac{s e c^{2} x}{2} + \frac{s e c^{3} x}{3} + c$

$19 \int_{1}^{\sqrt{e}} \frac{s i n (π l n x)}{x} d x S o l u t i o n : l e t u = π l n x \Rightarrow d x = \frac{d u}{\frac{π}{x}} = \frac{x}{π} d u \int \frac{s i n (π l n x)}{x} d x = \int \frac{s i n u}{x} \frac{x}{π} d u = \int \frac{s i n u}{x} \frac{x}{π} d u = \frac{1}{π} \int s i n u d u = - \frac{1}{π} c o s u = - \frac{1}{π} c o s (π l n x) \sqrt{e} 1 = - \frac{1}{π} (c o s (π l n \sqrt{e}) - c o s (π l n \sqrt{1})) = - \frac{1}{π} (c o s (\frac{π}{2}) - c o s (0)) = - \frac{1}{π} (0 - 1) = \frac{1}{π}$

$20 \int_{0}^{\frac{π}{2}} x s i n x^{2} d x S o l u t i o n : l e t u = x^{2} \Rightarrow d x = \frac{d u}{2 x} \int x s i n x^{2} d x = \int x s i n u \frac{d u}{2 x} = \frac{1}{2} \int x s i n u \frac{d u}{x} = \frac{1}{2} \int s i n u d u = - \frac{1}{2} c o s u = - \frac{1}{2} c o s u = - \frac{1}{2} c o s x^{2} \frac{π}{2} 0 = - \frac{1}{2} ({c o s {(\frac{π}{2})}^{2} - c o s (0)}^{2}) = - \frac{1}{2} (c o s {(\frac{π}{2})}^{2} - 1)$

$21 \int_{0}^{1} \frac{x^{3}}{\sqrt{x^{2} + 1}} d x S o l u t i o n : l e t u = x^{2} + 1 \Rightarrow d x = \frac{d u}{2 x} a n d x^{2} = u - 1 \int \frac{x^{3}}{\sqrt{x^{2} + 1}} d x = \int x^{3} u^{\frac{- 1}{2}} \frac{d u}{2 x} = \frac{1}{2} \int x^{2} u^{\frac{- 1}{2}} d u = \frac{1}{2} \int (u - 1) u^{\frac{- 1}{2}} d u = \frac{1}{2} \int (u^{\frac{1}{2}} - u^{- \frac{1}{2}}) d u = \frac{1}{3} u^{\frac{3}{2}} - u^{\frac{1}{2}} = \frac{1}{3} {(x^{2} + 1)}^{\frac{3}{2}} - {(x^{2} + 1)}^{\frac{1}{2}} 1 0 = \frac{1}{3} ({(2)}^{\frac{3}{2}} - 1) - {((2)}^{\frac{1}{2}} - 1) = \frac{\sqrt{8}}{3} + \frac{2}{3} - \sqrt{2}$

$22 \int_{0}^{\frac{π}{3}} s e c^{2} x t a n^{5} x d x S o l u t i o n : l e t u = t a n x \Rightarrow d x = \frac{d u}{s e c^{2} x} \int s e c^{2} x t a n^{5} x d x = \int s e c^{2} x u^{5} \frac{d u}{s e c^{2} x} = \int s e c^{2} x u^{5} \frac{d u}{s e c^{2} x} = \int u^{5} d u = \frac{1}{6} u^{6} = \frac{1}{6} t a n^{6} x \frac{π}{3} 0 = \frac{1}{6} (t a n^{6} (\frac{π}{3}) - 0) = \frac{9}{2}$

$23 \int_{0}^{2} (x - 1) e^{{(x - 1)}^{2}} d x S o l u t i o n : l e t u = {(x - 1)}^{2} \Rightarrow d x = \frac{d u}{2 (x - 1)} \int (x - 1) e^{{(x - 1)}^{2}} d x = \int (x - 1) e^{u} \frac{d u}{2 (x - 1)} = \frac{1}{2} \int (x - 1) e^{u} \frac{d u}{(x - 1)} = \frac{1}{2} \int e^{u} d u = \frac{1}{2} e^{u} = \frac{1}{2} e^{{(x - 1)}^{2}} 2 0 = \frac{1}{2} (e - e) = 0$

$24 \int_{1}^{4} \frac{\sqrt{\sqrt{x} + 2}}{\sqrt{x}} d x S o l u t i o n : l e t u = \sqrt{x} + 2 \Rightarrow d x = 2 \sqrt{x} d u \int \frac{\sqrt{\sqrt{x} + 2}}{\sqrt{x}} d x = \int \frac{\sqrt{u}}{\sqrt{x}} 2 \sqrt{x} d u = 2 \int \sqrt{u} d u = 2 \int (u^{\frac{1}{2}}) d u = \frac{4}{3} u^{\frac{3}{2}} = \frac{4}{3} {(\sqrt{x} + 2)}^{\frac{3}{2}} 4 0 = \frac{4}{3} (8 - \sqrt{27})$

$25 \int_{0}^{1} \frac{10 \sqrt{x}}{{(\sqrt{x^{3}} + 1)}^{2}} d x S o l u t i o n : \int \frac{10 \sqrt{x}}{{(\sqrt{x^{3}} + 1)}^{2}} d x = \int \frac{10 \sqrt{x}}{{({(\sqrt{x})}^{3} + 1)}^{2}} d x l e t u = \sqrt{x} \Rightarrow d x = \frac{d u}{\frac{1}{2 \sqrt{x}}} = 2 \sqrt{x} d u = 2 u d u \int \frac{10 \sqrt{x}}{{({(\sqrt{x})}^{3} + 1)}^{2}} d x = \int \frac{10 u}{{(u^{3} + 1)}^{2}} 2 u d u = 20 \int \frac{u^{2}}{{(u^{3} + 1)}^{2}} d u N o w l e t v = u^{3} + 1 \Rightarrow d u = \frac{d v}{3 u^{2}} = 20 \int \frac{u^{2}}{v^{2}} \frac{d v}{3 u^{2}} = \frac{20}{3} \int \frac{u^{2}}{v^{2}} \frac{d v}{u^{2}} = \frac{20}{3} \int \frac{u^{2}}{v^{2}} \frac{d v}{u^{2}} = \frac{20}{3} \int v^{- 2} d v = - \frac{20}{3 v} = - \frac{20}{3 (u^{3} + 1)} = - \frac{10}{3 ({(\sqrt{x})}^{3} + 1)} 1 0 = - \frac{20}{6} + \frac{20}{3} = \frac{10}{3}$

$26 \int_{0}^{\frac{π}{6}} 2^{c o s x} s i n x d x S o l u t i o n : l e t u = c o s x \Rightarrow d x = - \frac{d u}{s i n x} \int 2^{c o s x} s i n x d x = - \int 2^{u} s i n x \frac{d u}{s i n x} = - \int 2^{u} s i n x \frac{d u}{s i n x} = - \int 2^{u} d u = - \frac{2^{u}}{l n 2} = - \frac{2^{c o s x}}{l n 2} \frac{π}{6} 0 = - \frac{2^{c o s (\frac{π}{6})} - 2^{c o s (0)}}{l n 2} = \frac{1 - 2^{\frac{\sqrt{3}}{2}}}{l n 2}$

$27 \int_{\frac{π}{4}}^{\frac{π}{2}} c s c^{2} x c o t^{5} d x S o l u t i o n : l e t u = c o t x \Rightarrow d x = - \frac{d u}{c s c^{2} x} \int c s c^{2} x c o t^{5} d x = - \int c s c^{2} x u^{5} \frac{d u}{c s c^{2} x} = - \int c s c^{2} x u^{5} \frac{d u}{c s c^{2} x} = - \int u^{5} d u = - \frac{1}{6} u^{6} = - \frac{1}{6} c o t^{6} x \frac{π}{2} \frac{π}{4} = - \frac{1}{6} (c o t^{6} (\frac{π}{2}) - c o t^{6} (\frac{π}{4})) = - \frac{1}{6} (0 - 1) = \frac{1}{6}$

أجد مساحة المنطقة المظللة في كلٍ من التمثيلات البيانية الآتية :

$28 S o l u t i o n : A = \int_{- 1}^{0} 6 x {(x^{2} + 3)}^{3} d x + \int_{0}^{1} 6 x {(x^{2} + 3)}^{3} d x = 2 \int_{0}^{1} 6 x {(x^{2} + 3)}^{3} d x l e t u = x^{2} + 3 \Rightarrow d x = \frac{d u}{2 x} 2 \int 6 x {(x^{2} + 3)}^{3} = 2 \int 6 x u^{3} \frac{d u}{2 x} = 6 \int x u^{3} \frac{d u}{x} = 6 \int u^{3} d u = \frac{3}{2} u^{4} = \frac{3}{2} {(x^{2} + 3)}^{4} 1 0 = \frac{3}{2} (256 - 81) = 262.5$

$29 S o l u t i o n : A = \int_{2}^{4} \frac{x}{{(x - 1)}^{3}} d x A = \int_{2}^{4} x {(x - 1)}^{- 3} d x l e t u = x - 1 \Rightarrow d x = d u x = u + 1 \int x {(x - 1)}^{- 3} d x = \int x u^{- 3} d u = \int (u + 1) u^{- 3} d u = \int (u^{- 2} + u^{- 3}) d u = - \frac{1}{u} - \frac{1}{2 u^{2}} 4 2 = - (\frac{1}{4} - \frac{1}{2}) - (\frac{1}{32} - \frac{1}{8}) = \frac{1}{4} + \frac{3}{32} = \frac{11}{32}$

$30 S o l u t i o n : A = \int_{- 1}^{0} x e^{x^{2}} d x + \int_{0}^{2} x e^{x^{2}} d x l e t u = x^{2} \Rightarrow d x = \frac{d u}{2 x} A = \int_{1}^{0} x e^{u} \frac{d u}{2 x} + \int_{0}^{4} x e^{u} \frac{d u}{2 x} = \frac{1}{2} \int_{1}^{0} x e^{u} \frac{d u}{x} + \frac{1}{2} \int_{0}^{4} x e^{u} \frac{d u}{x} = \frac{1}{2} e^{u} 0 1 + \frac{1}{2} e^{u} 4 0 = | \frac{1}{2} (e^{0} - e^{1}) | + \frac{1}{2} (e^{4} - e^{0}) = \frac{e^{4} + e - 2}{2}$

$31 S o l u t i o n : A = \int_{0}^{\sqrt{\frac{π}{6}}} 2 x c o s (x^{2} + \frac{π}{6}) d x l e t u = x^{2} + \frac{π}{6} \Rightarrow d x = \frac{d u}{2 x} A = \int 2 x c o s u \frac{d u}{2 x} = \int 2 x c o s u \frac{d u}{2 x} = s i n u = s i n (x^{2} + \frac{π}{6}) \sqrt{\frac{π}{6}} 0 = s i n (\frac{2 π}{6}) - s i n (0 + \frac{π}{6}) = \frac{\sqrt{3}}{2} - \frac{1}{2} = \frac{\sqrt{3} - 1}{2}$

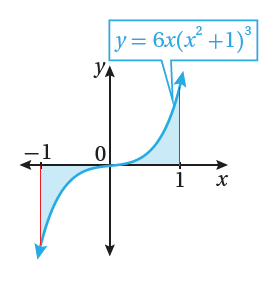
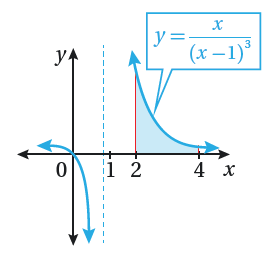
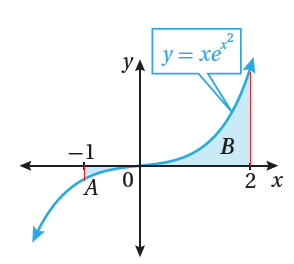
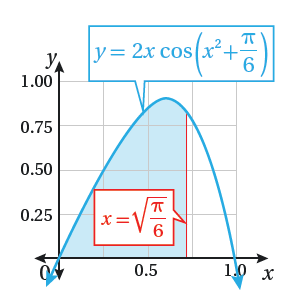
في كلٍ مما يأتي المشتقة الأولى للاقتران f(x) ونقطة يمر بها منحنى y=f(x) .

إستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران .

$32 f' (x) = 2 x {(4 x^{2} - 10)}^{2}, (2, 10) S o l u t i o n : f (x) = \int 2 x {(4 x^{2} - 10)}^{2} d x l e t u = 4 x^{2} - 10 \Rightarrow d x = \frac{d u}{8 x} f (x) = \int 2 x u^{2} \frac{d u}{8 x} = \frac{1}{4} \int x u^{2} \frac{d u}{x} = \frac{1}{12} u^{3} f (x) = \frac{1}{12} {(4 x^{2} - 10)}^{3} + c b u t f (2) = 10 t o s o l v e c f (x) = \frac{1}{12} (216) + c = 10 18 + c = 10 \Rightarrow c = - 8 T h e n f (x) = \frac{1}{12} {(4 x^{2} - 10)}^{3} - 8$

$33 f' (x) = x^{2} e^{- 0.2 x^{3}}, (0, \frac{3}{2}) S o l u t i o n : f (x) = \int x^{2} e^{- 0.2 x^{3}} d x l e t u = - 0.2 x^{3} - 10 \Rightarrow d x = \frac{d u}{- 0.6 x^{2}} f (x) = \int x^{2} e^{u} \frac{d u}{- 0.6 x^{2}} = - \frac{1}{0.6} \int x^{2} e^{u} \frac{d u}{x^{2}} = - \frac{1}{0.6} e^{u} = - \frac{1}{0.6} e^{- 0.2 x^{3}} + c f (x) = - \frac{1}{0.6} e^{- 0.2 x^{3}} + c b u t f (0) = \frac{3}{2} t o s o l v e c f (0) = - \frac{1}{0.6} e^{0} + c = \frac{3}{2} - \frac{5}{3} + c = \frac{3}{2} \Rightarrow c = \frac{19}{6} T h e n f (x) = - \frac{1}{0.6} e^{- 0.2 x^{3}} + \frac{19}{6}$

يبين الشكل المجاور جزءا من منحنى الاقتران 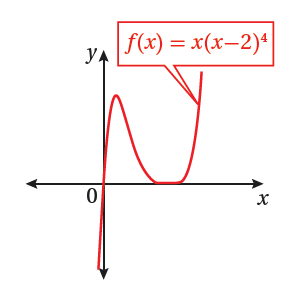$f (x) = x {(x - 2)}^{4}$

$34$ أجد إحداثيي نقطة تماس الاقتران مع محور x .

من الشكل x = 2 .

$35$ أجد مساحة المنطقة المحصورة بين منحنى الاقتران ومحور x .

$S o l u t i o n : A = \int_{0}^{2} x {(x - 2)}^{4} d x l e t u = x - 2 \Rightarrow d x = d u x = u + 2 A = \int (u + 2) u^{4} d u = \int (u^{5} + 2 u^{4}) d u = \frac{1}{6} u^{6} + \frac{2}{5} u^{5} = \frac{1}{6} {(x - 2)}^{6} + \frac{2}{5} {(x - 2)}^{5} 2 0 = - \frac{64}{6} + \frac{64}{5} = \frac{64}{30}$

$36$ يتحرك جسيم في خط مستقيم ، وتعطى سرعته المتجهة بالاقتران : $v (t) = s i n w t c o s^{2} w t$

حيث t الزمن بالثواني ، و v سرعته المتجهة بالمتر لكل ثانية ، و w ثابت .

إذا انطلق الجسيم من نقطة الأصل ، فأجد موقعه بعد t ثانية .

$S o l u t i o n : \int v (t) d t = \int s i n w t c o s^{2} w t d t s (t) = \int s i n w t c o s^{2} w t d t l e t u = c o s w t \Rightarrow d t = - \frac{d u}{w s i n w t} \int s i n w t c o s^{2} w t d t = - \int s i n w t u^{2} \frac{d u}{w s i n w t} = - \int s i n w t u^{2} \frac{d u}{w s i n w t} = - \frac{1}{w} \int u^{2} d u = - \frac{u^{3}}{3 w} + c = - \frac{c o s^{3} w t}{3 w} + c t o s o l v e c s (t) = - \frac{c o s^{3} w t}{3 w} + c s (t) = - \frac{c o s^{3} w (0)}{3 w} + c = 0 \Rightarrow c = \frac{1}{3 w} s (t) = \frac{1}{3 w} - \frac{c o s^{3} w t}{3 w}$

$37$ يمثل الاقتران C(t) تركيز دواء في الدم بعد t دقيقة من حقنه في جسم مريض ،

حيث C مقاسة بالملغرام لكل سنتمتر مكعب (cm3/mg ) .

إذا كان تركيز الدواء لحظة حقنه في جسم المريض $0.5 m g / c m^{3}$ ،

وأخذ يتغير بمعدل $C' (t) = \frac{- 0.01 e^{- . 001 t}}{{(1 + e^{- 0.01 t})}^{2}}$ . فأجد C(t)

$S o l u t i o n : C (t) = \int \frac{- 0.01 e^{- . 001 t}}{{(1 + e^{- 0.01 t})}^{2}} d t l e t u = 1 + e^{- 0.01 t} \Rightarrow d t = - \frac{d u}{e^{- 0.01 t}} C (t) = - 0.01 \int \frac{e^{- . 001 t}}{u^{2}} \frac{d u}{e^{- 0.01 t}} = - 0.01 \int \frac{e^{- . 001 t}}{u^{2}} \frac{d u}{e^{- 0.01 t}} = - 0.01 \int \frac{1}{u^{2}} d u = - 0.01 \int u^{- 2} d u = \frac{0.01}{u} = \frac{0.01}{1 + e^{- 0.01 t}} + c b u t C (0) = 0.5 t o s o l v e c C (t) = \frac{0.01}{1 + e^{- 0.01 t}} + c C (0) = \frac{0.01}{1 + e^{- 0.01 (0)}} + c = 0.5 \frac{0.01}{2} + c = 0.5 0.005 + c = 0.5 \Rightarrow c = 0.495 C (t) = \frac{0.01}{1 + e^{- 0.01 t}} + 0.495$

$38$ أجد قيمة $\int_{l n 3}^{l n 4} \frac{e^{4 x}}{e^{x} - 2} d x$ ، ثم أكتب الإجابة بالصيغة $\frac{a}{b} + c l n d$

حيث a .b . c. d ثوابت صحيحة

$S o l u t i o n : \int \frac{e^{4 x}}{e^{x} - 2} d x = \int \frac{{(e^{x})}^{4}}{e^{x} - 2} d x l e t u = e^{x} \Rightarrow d x = \frac{d u}{e^{x}} = \frac{d u}{u} \int \frac{{(e^{x})}^{4}}{e^{x} - 2} d x = \int \frac{u^{4}}{u - 2} \frac{d u}{u} = \int \frac{u^{3}}{u - 2} d u = \int (u^{2} + 2 u + 4 + \frac{8}{u - 2}) d u = (\frac{u^{3}}{3} + u^{2} + 4 u + 8 l n (u - 2)) = (\frac{e^{3 x}}{3} + e^{2 x} + 4 e^{x} + 8 l n (e^{x} - 2)) \ln 4 \ln 3 = (\frac{e^{3 l n 4}}{3} + e^{2 l n 4} + 4 e^{l n 4} + 8 l n (e^{l n 4} - 2)) - (\frac{e^{3 l n 3}}{3} + e^{2 l n 3} + 4 e^{l n 3} + 8 l n (e^{l n 3} - 2)) = (\frac{64}{3} + 16 + 16 + 8 l n (2)) - (\frac{27}{3} + 9 + 12) = (\frac{37}{3} + 11 + 8 l n (2)) = \frac{70}{3} + 8 l n 2$

$39$ إذا كان $f' (x) = t a n x$ ، وكان $f (3) = 5$ ، فأثبت أن: $f (x) = l n |\frac{c o s 3}{c o s x}| + 5$

$f' (x) = t a n x, f (3) = 5 S o l u t i o n : f (x) = \int t a n x d x = \int \frac{\sin x}{\cos x} d x = - l n (\cos x) + c b u t f (3) = 5 \Rightarrow 5 = - \ln (\cos 3) + c \Rightarrow c = 5 + \ln (\cos 3) f (x) = - l n (\cos x) + 5 + l n (\cos 3) = l n |\frac{c o s 3}{c o s x}| + 5$

تبرير : إذا كان الشكل المجاور يمثل منحنى الاقتران $f (x) = 3 c o s x \sqrt{1 + s i n x}$

فأجيب عن الاسئلة التالية تباعاً :

$40$ أجد قيمة كل من A . B . C .D .

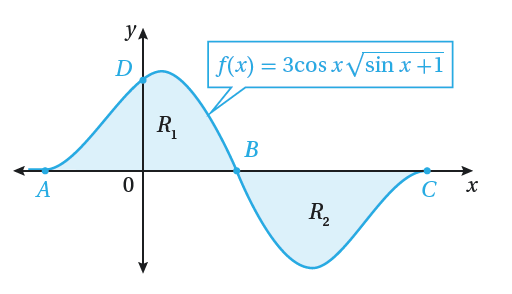
$S o l u t i o n : f (x) = 3 c o s x \sqrt{1 + s i n x} = 0 \Rightarrow 3 c o s x = 0 O r \sqrt{1 + s i n x} = 0 c o s x = 0 \Rightarrow x = - \frac{π}{2}, x = \frac{π}{2} 1 + s i n x = 0 s i n x = - 1 \Rightarrow x = \frac{3 π}{2} t h e n A = - \frac{π}{2}, B = 0 a n d C = \frac{π}{2} n o w t o s o l v e D : f (x) = 3 c o s x \sqrt{1 + s i n x} f (0) = 3 c o s (0) \sqrt{1 + s i n (0)} = 3$

$41$ أجد مساحة المنطقة المظللة .

$S o l u t i o n : A = A_{1} + A_{2} = 2 A_{1} b e c a u s e o f s y m e t r i c A_{1} = \int_{- \frac{π}{2}}^{\frac{π}{2}} 3 c o s x \sqrt{1 + s i n x} d x l e t u = 1 + s i n x \Rightarrow d x = \frac{d u}{c o s x} A_{1} = \int 3 c o s x {(1 + s i n x)}^{\frac{1}{2}} d x = \int 3 c o s x {(u)}^{\frac{1}{2}} \frac{d u}{c o s x} = 3 \int u^{\frac{1}{2}} d u = 2 u^{\frac{3}{2}} = 2 {(1 + s i n x)}^{\frac{3}{2}} \frac{π}{2} - \frac{π}{2} = 2 {(1 + s i n (\frac{π}{2}))}^{\frac{3}{2}} - 2 {(1 + s i n (- \frac{π}{2}))}^{\frac{3}{2}} = 2 \sqrt{8} A = 2 A_{1} = 4 \sqrt{8}$

$42$ أبين أن للمنطقة $R_{1}, R_{2}$ المساحة نفسها .

$S o l u t i o n : A_{1} = \int_{- \frac{π}{2}}^{\frac{π}{2}} 3 c o s x \sqrt{1 + s i n x} d x = 2 \sqrt{8} A_{2} = \int_{\frac{π}{2}}^{3 \frac{π}{2}} 3 c o s x \sqrt{1 + s i n x} d x = | - 2 \sqrt{8} | = 2 \sqrt{8}$

$43$ تحد: أجد قيمة

$\int_{1}^{16} \frac{\sqrt{x}}{\sqrt[4]{x^{3}} + 1} d x S o l u t i o n : \int \frac{\sqrt{x}}{\sqrt[4]{x^{3}} + 1} d x = \int \frac{x^{\frac{1}{2}}}{x^{\frac{3}{4}} + 1} d x l e t u = x^{\frac{3}{4}} + 1 \Rightarrow d x = \frac{d u}{\frac{3}{4} x^{\frac{- 1}{4}}} = \frac{4}{3} x^{\frac{1}{4}} d u B u t x^{\frac{3}{4}} = u - 1 \int \frac{x^{\frac{1}{2}}}{x^{\frac{3}{4}} + 1} d x = \int \frac{x^{\frac{1}{2}}}{u} \times \frac{4}{3} x^{\frac{1}{4}} d u = \frac{4}{3} \int \frac{x^{\frac{3}{4}}}{u} d u = \frac{4}{3} \int \frac{u - 1}{u} d u = \frac{4}{3} \int (1 - \frac{1}{u}) d u = \frac{4}{3} (u - l n u) = \frac{4}{3} (x^{\frac{3}{4}} + 1 - l n (x^{\frac{3}{4}} + 1)) 16 1 = \frac{4}{3} (9 - l n (9)) - \frac{4}{3} (2 - l n (2)) = 12 - \frac{4}{3} l n (9) - \frac{8}{3} + \frac{4}{3} l n (2) = \frac{28}{3} + \frac{4}{3} l n \frac{2}{9}$

$44$ تبرير : أذا كان f متصلا فأثبت أن : $\int_{0}^{\frac{π}{2}} f (c o s x) d x = \int_{0}^{\frac{π}{2}} f (s i n x) d x$

$S o l u t i o n : F o r \int_{0}^{\frac{π}{2}} f (c o s x) d x l e t u = \cos x \Rightarrow d x = \frac{d u}{- \sin x} B u t u^{2} = \cos^{2} x = 1 - \sin^{2} x \Rightarrow \sin x = \sqrt{1 - u^{2}} W h e n x = 0 \Rightarrow u = 1 x = \frac{π}{2} \Rightarrow u = 0 \int_{0}^{\frac{π}{2}} f (c o s x) d x = \int_{1}^{0} f (u) \frac{d u}{- s i n x} = \int_{0}^{1} \frac{f (u)}{\sqrt{1 - u^{2}}} d u . . . . * * F o r \int_{0}^{\frac{π}{2}} f (s i n x) d x l e t v = \sin x \Rightarrow d x = \frac{d v}{\cos x} B u t v^{2} = \sin^{2} x = 1 - \cos^{2} x \Rightarrow \cos x = \sqrt{1 - v^{2}} W h e n x = 0 \Rightarrow v = 0 x = \frac{π}{2} \Rightarrow v = 1 \int_{0}^{\frac{π}{2}} f (\sin x) d x = \int_{0}^{1} f (v) \frac{d v}{c o s x} = \int_{0}^{1} \frac{f (v)}{\sqrt{1 - v^{2}}} d v . . . . * * B o t h s i e d s h a v e s a m e f o r m u l a t h e r e f o r t h e y a r e e q u e l s .$

$45$ تبرير : أذا كان a . b عددين حقيقين موجبين فأثبت أن : $\int_{0}^{1} x^{a} {(1 - x)}^{b} d x = \int_{0}^{1} x^{b} {(1 - x)}^{a} d x$

$S o l u t i o n : l e t u = 1 - x \Rightarrow d x = d u x = 1 - u W h e n x = 0 \Rightarrow u = 1 x = 1 \Rightarrow u = 0 \int_{0}^{1} x^{a} {(1 - x)}^{b} d x = \int_{1}^{0} {(1 - u)}^{a} {(u)}^{b} d u = \int_{1}^{0} {u^{b} (1 - u)}^{a} d u$

تحد: أجد قيمة كل من التكاملات الآتية:

$46 \int \frac{1}{x l n x (l n (l n x))} d x S o l u t i o n : l e t u = \ln x \Rightarrow d x = \frac{d u}{\frac{1}{x}} = x d u \int \frac{1}{x l n x (l n (l n x))} d x = \int \frac{1}{x u (l n (u))} x d u = \int \frac{1}{x u (l n (u))} x d u = \int \frac{1}{u l n (u)} d u N o w l e t v = l n (u) \Rightarrow d u = \frac{d v}{\frac{1}{u}} = u d v \int \frac{1}{u l n (u)} d u = \int \frac{1}{u v} u d v = \int \frac{1}{u v} u d v = \int \frac{1}{v} d v = \ln v = \ln (\ln u) = \ln (\ln (\ln x)) + c$

$47 \int s i n 2 x {(1 + s i n x)}^{3} d x S o l u t i o n : \int 2 s i n x c o s x {(1 + s i n x)}^{3} d x l e t u = 1 + s i n x \Rightarrow d x = \frac{d u}{c o s x} = x d u a n d s i n x = u - 1 \int 2 s i n x c o s x {(1 + s i n x)}^{3} d x = \int 2 s i n x c o s x u^{3} \frac{d u}{c o s x} = 2 \int s i n x c o s x u^{3} \frac{d u}{c o s x} = 2 \int (u - 1) u^{3} d u = 2 \int (u^{4} - u^{3}) d u = \frac{2}{5} u^{5} - \frac{2}{4} u^{4} + c = \frac{2}{5} {(1 + s i n x)}^{5} - \frac{2}{4} {(1 + s i n x)}^{4} + c$

$48 \int \frac{1}{\sqrt{x} - \sqrt[3]{x}} d x S o l u t i o n : l e t u^{6} = x \Rightarrow 6 u^{5} d u = d x u^{3} = \sqrt{x} u^{2} = \sqrt[3]{x} \int \frac{1}{\sqrt{x} - \sqrt[3]{x}} d x = \int \frac{1}{u^{3} - u^{2}} 6 u^{5} d u = 6 \int \frac{u^{3}}{u - 1} d u = \int (6 u^{2} + 6 u + 6 + \frac{6}{u - 1}) d u = 2 u^{3} + 3 u^{2} + 6 u + 6 l n (u - 1) = 2 \sqrt{x} + 3 \sqrt[3]{x} + 6 \sqrt[6]{x} + 6 l n (\sqrt[6]{x} - 1) + c$

رياضيات فصل ثاني

التوجيهي علمي

التطبيق لنظام

MAC

التطبيق لنظام

WINDOWS