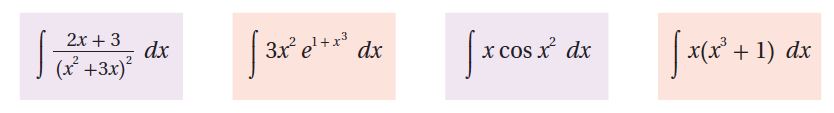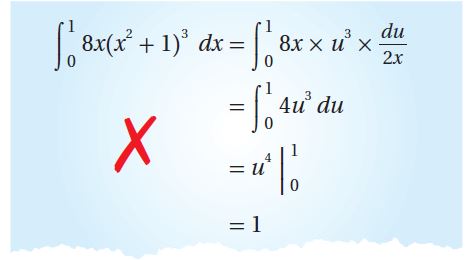الرياضيات فصل ثاني

حل أسئلة الدرس (6) التكامل بالتعويض

 

مسألة اليوم صفحة 54:

يمثل الاقتران $C\left(t\right)$ تركيز الدواء في الدم بعد $t$ ساعة من حقنه في جسم مريض،

حيث $C$ مقيسة بالمليغرام لكل سنتمتر مكعب $\left(mg /c{m}^3\right)$. إذا كان تركيز الدواء

في دم المريض يتغير بمعدل: $C \mathit{َ}\mathbf{ }\left(t\right)=\frac{0.3 t}{\sqrt{t^2+16}}$،فأجد مقدار التغير في تركيز الدواء

بالدم خلال الساعات الثلاث الأولى التي تلت حقنه في جسم المريض.

الحل:

الخطوة الأولى: أجد تكامل الاقتران $C \mathit{َ}\mathbf{ }\left(t\right)$ باستخدام طريقة التعويض:

                          $$\begin{gathered} C \left(t\right)=\int \frac{0.3 t}{\sqrt{t^2+16}} dt \\ let u=t^2+16 \Rightarrow \frac{du}{dt}=2t \\ \Rightarrow dt=\frac{du}{2t} \\ \therefore \int \frac{0.3 t}{\sqrt{t^2+16}} dt = \int \frac{0.3 t}{\sqrt{u}}\times \frac{du}{2t} \\ =\frac{0.3}{2}\int \frac{1}{u^{\frac{1}{2}}} du \\ =\frac{3}{20}\int u^{-\frac{1}{2}} du \\ =\frac{3}{20}\times 2u^{\frac{1}{2}} +K \\ =\frac{3}{10}\sqrt{u} +K \\ =0.3\sqrt{t^2+16} +K \end{gathered}$$

الخطوة الثانية: أجد ثابت التكامل C

بما أن مقدار تركيز الدواء في الدم في البداية هو 0 مليغرام، إذن $C\left(0\right)=0$ ومنه:

             $$\begin{gathered} C\left(t\right)=0.3\sqrt{t^2+16} +K \\ C\left(0\right)=0.3\sqrt{{\left(0\right)}^2+16} +K \\ 0=0.3\sqrt{16} +K \\ 0=0.3\left(4\right) +K \\ 0=1.2+K \\ \to K =-1.2 \end{gathered}$$

إذن، $C\left(t\right)=0.3\sqrt{t^2+16} -1.2$

الخطوة الثالثة:أجد مقدار التغير في تركيز الدواء بالدم خلال الساعات الثلاث

                         الأولى التي تلت حقنه في جسم المريض:

                        $$\begin{gathered} C\left(3\right)=0.3\sqrt{{\left(3\right)}^2+16} -1.2 \\ =0.3\sqrt{9+16}-1.2 \\ =0.3\sqrt{25} -1.2 \\ =0.3\left(5\right)-1.2 \\ =1.5-1.2 \\ =0.3 \end{gathered}$$

إذن مقدار التغير في تركيز الدواء بالدم خلال الساعات الثلاث الأولى من حقنه هي$0.3 mg/c{m}^3$

---

أتحقق من فهمي صفحة 58:

أجد كلًا من التكاملات الآتية:

                                                     $$\begin{gathered} a) \int 6x^2{(2x^3-3)}^4 dx \\ \hspace{0.17em} 2x^3-3=u \Rightarrow 6x^2 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{6 x^2} \\ \therefore \int 6x^2{(2x^3-3)}^4 dx=\int 6x^2{\left(u\right)}^4 \frac{du}{6 x^2} \\ =\int u^4 du \\ =\frac{u^5}{5}+C \\ =\frac{1}{5}{(2x^3-3)}^5+C \end{gathered}$$

 

 

                                                       $$\begin{gathered} b) \int x e^{x^2+1} dx \\ \hspace{0.17em} \\ x^2+1=u \Rightarrow 2x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2x} \\ \therefore \int x e^{{}^{x^2+1}} dx=\int x e^u \frac{du}{2x} \\ =\frac{1}{2}\int e^u du \\ =\frac{1}{2}{e}^u+C \\ =\frac{1}{2}{e}^{x^2+1}+C \end{gathered}$$

                                                 

 

                                                    $$\begin{gathered} c) \int \frac{4x+8}{\sqrt{2x^2+8x}} dx \\ \hspace{0.17em} \\ 2x^2+8x=u \Rightarrow 4x+8 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{4x+8} \\ \therefore \int \frac{4x+8}{\sqrt{2x^2+8x}} dx=\int \frac{4x+8}{\sqrt{u}} \times \frac{du}{4x+8} \\ =\int \frac{1}{\sqrt{u}} du=\int u^{-\frac{1}{2}} du \\ =2u^{\frac{1}{2}}+C \\ =2\sqrt{2x^2+8x}+C \end{gathered}$$

 

                                         $$\begin{gathered} d) \int \frac{{(\ln x)}^2}{x} dx \\ \hspace{0.17em} \\ \ln x=u \Rightarrow \frac{1}{x} = \frac{du}{dx} \\ \Rightarrow dx = x du \\ \therefore \int \frac{{(ln x)}^2}{x} dx=\int \frac{u^2}{x}\times x du \\ =\int u^2 du \\ =\frac{u^3}{3}+C \\ =\frac{1}{3}{(\ln x)}^3+C \end{gathered}$$

                

                                            $$\begin{gathered} e) \int x^3 \cos (x^4-5) dx \\ \hspace{0.17em} \\ x^4-5=u \Rightarrow 4x^3 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{4x^3} \\ \therefore \int x^3 \cos (x^4-5) dx=\int x^3 \cos \left(u\right) \frac{du}{4x^3} \\ =\frac{1}{4}\int \cos u du \\ =\frac{1}{4}\sin u+C \\ =\frac{1}{4} \sin (x^4-5)+C \end{gathered}$$

 

 

                                 $$\begin{gathered} f) \int co{s}^4 x sin x dx \\ \hspace{0.17em} \\ cos x=u \Rightarrow -sin x = \frac{du}{dx} \\ \Rightarrow dx =- \frac{du}{sin x} \\ \therefore \int co{s}^4 x sin x dx=\int u^4 sin x \times -\frac{du}{sin x} \\ =-\int u^4 du \\ =-\frac{1}{5}{u}^5+C \\ =-\frac{1}{5} co{s}^{5}x+C \end{gathered}$$

---

أتحقق من فهمي صفحة 60:

تجارة:يمثل الاقتران $p\left(x\right)$ سعر القطعة الواحدة (بالدينار) من منتج معين،

         حيث $x$ عدد القطع المبيعة (بالمئات) من المنتج.

         إذا كان: $p\mathit{َ}\mathbf{ }\left(x\right)=\frac{-300x}{\sqrt{{\left(36+x^2\right)}^3}}$ هو معدل التغير في سعر القطعة

        الواحدة من المنتج، فأجد $p\left(x\right)$ ، علمًا بأن سعر القطعة الواحدة $JD 75$

        عندما يكون عدد القطع المبيعة 800 قطعة.

الحل:

الخطوة الأولى: أجد تكامل الاقتران:$pَ\mathbf{ }\left(x\right)$

                          $$\begin{gathered} p\left(x\right)=\int \frac{-300x}{\sqrt{{(36+x^2)}^3}}dx \\ 36+x^2=u \Rightarrow 2x =\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{2x} \\ \therefore \int \frac{-300x}{\sqrt{{(36+x^2)}^3}}dx=\int \frac{-300 x}{\sqrt{u^3}}\times \frac{du}{2x} \\ =\frac{-300}{2}\int \frac{1}{u^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}du \\ =-150\int u^{-\frac{3}{2}} du \\ =-150 \left(-2\right) u^{-\frac{1}{2}} +C \\ =300 {\left(36+x^2\right)}^{-\frac{1}{2}}+C \\ =\frac{300}{\sqrt{36+x^2}}+C \end{gathered}$$

الخطوة الثانية: أجد ثابت التكامل C:

بما أن سعر القطعة الواحدة هو 75 دينارًا عندما يكون عدد القطع المبيعة 800قطعة،

  فإن:$p\left(8\right)=75$ (لأن قيمة $x$ بالمئات) ،ومنه:

                    $$\begin{gathered} p\left(8\right)=\frac{300}{\sqrt{36+{\left(8\right)}^2}}+C \\ 75=\frac{300}{\sqrt{36+64}}+C \\ 75=\frac{300}{\sqrt{100}}+C \\ 75=\frac{300}{10}+C \\ 75=30+C \\ 75-30=C \\ 45=C \end{gathered}$$

إذن، $p\left(x\right)=\frac{300}{\sqrt{36+x^2}}+45$

---

أتحقق من فهمي صفحة 62:

أجد كلًا من التكاملات الآتية:

                    $$\begin{gathered} a) {\int }_0^1{x}^2{(x^3-1)}^4 dx \\ x^3-1=u\Rightarrow 3x^2=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{3x^2} \\ x=0 \Rightarrow u=-1 \\ x=1\Rightarrow u=0 \\ \therefore {\int }_0^{1 }{x}^2{(x^3-1)}^4 dx ={\int }_{-1}^0{x}^2 {\left(u\right)}^4 \frac{du}{3x^2} \\ =\frac{1}{3}{\int }_{-1}^0{u}^4 du \\ =\frac{1}{3}\left(\frac{u^5}{5}\right)\overline{)\begin{array}{c}0\\ -1\end{array}} \\ =\frac{1}{15}\left(0^5-{\left(-1\right)}^5\right) \\ =\frac{1}{15} \end{gathered}$$

 

                     $$\begin{gathered} b) {\int }_{-1}^0\frac{x^3}{{(2-x^4)}^7} dx \\ 2-x^4=u\Rightarrow -4x^3=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{-4x^3} \\ x=-1 \Rightarrow u=2-{\left(-1\right)}^4=1 \\ x=0 \Rightarrow u=2-{\left(0\right)}^4=2 \\ \therefore {\int }_{-1}^{0 }\frac{x^3}{{(2-x^4)}^7} dx ={\int }_1^2\frac{x^3}{{\left(u\right)}^7} \frac{du}{-4x^3} \\ =-\frac{1}{4}{\int }_1^2\frac{1}{u^7} du \\ =-\frac{1}{4}{\int }_1^2{u}^{-7} du=-\frac{1}{4}\left(\frac{u^{-6}}{-6}\right)\overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\frac{1}{24}(\frac{1}{u^6})\overline{)\begin{array}{c}2\\ 1\end{array}}=\frac{1}{24}\left(\frac{1}{2^6}-\frac{1}{1^6}\right) \\ =\frac{1}{24}\left(\frac{1}{64}-1\right)=\frac{1}{24}\left(-\frac{63}{64}\right) =-\frac{21}{512} \end{gathered}$$

 

              $$\begin{gathered} c) {\int }_1^e\frac{\ln x}{x} dx \\ \ln x=u\Rightarrow \frac{1}{x}=\frac{du}{dx} \\ \Rightarrow dx=xdu \\ x=1 \Rightarrow u=\ln 1=0 \\ x=e \Rightarrow u=\ln e=1 \\ \therefore {\int }_1^{e }\frac{ln x}{x} dx ={\int }_0^1\frac{u}{x} x du \\ ={\int }_0^{1}u du \\ =\frac{1}{2}\left(u^2\right)\overline{)\begin{array}{c}1\\ 0\end{array}} \\ =\frac{1}{2}\left(1^2-0^2\right) \\ =\frac{1}{2} \end{gathered}$$

---

أتدرب وأحل المسائل صفحة 62:

أجد كلًّا من التكاملات الآتية:

                                        $$\begin{gathered} 1) \int \frac{x}{\sqrt{x^2+4}} dx \\ \hspace{0.17em} \\ x^2+4=u \Rightarrow 2x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2x} \\ \therefore \int \frac{x}{\sqrt{x^2+4}} dx=\int \frac{x}{\sqrt{u}} \times \frac{du}{2x} \\ =\frac{1}{2}\int \frac{1}{\sqrt{u}} du=\frac{1}{2}\int u^{-\frac{1}{2}} du \\ =\frac{2}{2}{u}^{\frac{1}{2}}+C \\ =\sqrt{x^2+4}+C \end{gathered}$$    

---

                 $$\begin{gathered} 2) \int x^2{(2x^3+5)}^4 dx \\ Solution:\hspace{0.17em} \\ let 2x^3+5=u \Rightarrow 6x^2 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{6 x^2} \\ \therefore \int x^2{(2x^3+5)}^4 dx=\int x^2{\left(u\right)}^4 \frac{du}{6 x^2} \\ =\frac{1}{6}\int u^4 du \\ =\frac{1}{6}\left(\frac{u^5}{5}\right)+C \\ =\frac{1}{30}{(2x^3+5)}^5+C \end{gathered}$$

---

                               $$\begin{gathered} 3) \int 3x\sqrt{x^2+7} dx \\ Solution:\hspace{0.17em} \\ let x^2+7=u \Rightarrow 2x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2 x} \\ \therefore \int 3x\sqrt{x^2+7} dx=\int 3\sqrt{u} \frac{du}{2x} \\ =\frac{3}{2}\int u^{\frac{1}{2}} du \\ =\frac{3}{2}\left(\frac{2}{3}{u}^{\frac{3}{2}}\right)+C \\ =\sqrt{u^3}+C \\ =\sqrt{{\left(x^2+7\right)}^3}+C \end{gathered}$$

---

                          $$\begin{gathered} 4) \int x^6 e^{1-x^7} dx \\ \hspace{0.17em} \\ 1-x^7=u \Rightarrow -7x^6 = \frac{du}{dx} \\ \Rightarrow dx = -\frac{du}{7 x^6} \\ \therefore \int x^6 e^{{}^{1-x^7}} dx=\int x^6 e^u \frac{-du}{7 x^6} \\ =-\frac{1}{7}\int e^u du \\ =-\frac{1}{7}{e}^u+C \\ =-\frac{1}{7}{e}^{1-x^7}+C \end{gathered}$$

---

                     $$\begin{gathered} 5) \int \frac{x^4}{{(x^5+9)}^3} dx \\ x^5+9=u\Rightarrow 5x^4=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{5x^4} \\ \therefore \int \frac{x^4}{{(x^5+9)}^3} dx =\int \frac{x^4}{{\left(u\right)}^3} \frac{du}{5x^4} \\ =\frac{1}{5}\int \frac{1}{u^3} du \\ =\frac{1}{5}\int u^{-3} du=\frac{1}{5}(\frac{u^{-2}}{-2}) +C \\ =-\frac{1}{10 u^2} +C \\ =-\frac{1}{10{\left(x^5+9\right)}^2}+C \end{gathered}$$

            

---

               

                         $$\begin{gathered} 6) \int \left(3x^2-1\right) e^{x^3-x} dx \\ \hspace{0.17em} \\ x^3-x=u \Rightarrow 3x^2-1 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{3x^2-1} \\ \therefore \int \left(3x^2-1\right) e^{{}^{x^3-x}} dx=\int (3x^2-1) e^u \frac{du}{\left(3x^2-1\right)} \\ =\int e^u du \\ =e^u+C \\ =e^{x^3-x}+C \end{gathered}$$

 

---

                   $$\begin{gathered} 7) \int \frac{3x-3}{\sqrt{x^2-2x+4}} dx \\ \hspace{0.17em} \\ x^2-2x+4=u \Rightarrow 2x-2 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2x-2} \\ \therefore \int \frac{3x-3}{\sqrt{x^2-2x+4}} dx=\int \frac{3x-3}{\sqrt{u}} \times \frac{du}{2x-2} \\ =\int \frac{3\left(x-1\right)}{\sqrt{u}} \times \frac{du}{2\left(x-1\right)} \\ =\frac{3}{2}\int \frac{1}{\sqrt{u}} du=\frac{3}{2}\int u^{-\frac{1}{2}} du \\ =\frac{3}{2}\left(2 u^{\frac{1}{2}}\right)+C \\ =3\sqrt{x^2-2x+4 } +C \end{gathered}$$

 

---

                            $$\begin{gathered} 8) \int \frac{1}{x lnx} dx \\ \hspace{0.17em} \\ ln x=u \Rightarrow \frac{1}{x} = \frac{du}{dx} \\ \Rightarrow dx = x du \\ \therefore \int \frac{1}{x lnx} dx=\int \frac{1}{x u}\times x du \\ =\int \frac{1}{u} du \\ =ln \left|u\right|+C \\ =ln \left|ln x\right|+C \end{gathered}$$

 

---

                        $$\begin{gathered} 9) \int sin x{(1+cos x)}^4 dx \\ \hspace{0.17em} \\ 1+cos x=u \Rightarrow -sin x = \frac{du}{dx} \\ \Rightarrow dx = -\frac{du}{sin x} \\ \therefore \int sin x{ (1+cos x)}^4 dx=\int sin x {\left(u\right)}^4 \frac{-du}{sin x} \\ =-\int u^4 du \\ =-\frac{u^5}{5}+C \\ =-\frac{1}{5} {(1+cos x)}^5+C \end{gathered}$$

---

                  $$\begin{gathered} 10) \int si{n}^5 2x cos 2x dx \\ \hspace{0.17em} \\ sin 2x=u \Rightarrow 2 cos 2x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2 cos 2x} \\ \therefore \int { (sin 2x)}^5 cos 2x dx=\int {\left(u\right)}^5 cos 2x \times \frac{du}{2 cos 2x} \\ =\frac{1}{2}\int u^5 du \\ =\frac{1}{2}\left(\frac{u^6}{6}\right)+C \\ =\frac{1}{12} u^6+C \\ =\frac{1}{12} {\left(sin 2x\right)}^6 +C \end{gathered}$$

---

                     $$\begin{gathered} 11) \int \frac{sin \left(\frac{1}{x}\right)}{x^2 } dx \\ \hspace{0.17em} \\ \frac{1}{x}=u \Rightarrow -\frac{1}{x^2} = \frac{du}{dx} \\ \Rightarrow dx = -x^2 du \\ \therefore \int \frac{sin \left(\frac{1}{x}\right)}{x^2 } dx=\int \frac{sin u}{x^2 }\times -x^2 du \\ =-\int sin u du \\ =-\left(- \cos u\right)+C \\ =cos \left(\frac{1}{x}\right)+C \end{gathered}$$

---

 

                        $$\begin{gathered} 12) \int \frac{cos x}{e^{sin x} } dx \\ \hspace{0.17em} \\ sin x=u \Rightarrow \cos x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{\cos x} \\ \therefore \int \frac{\cos x}{e^{sin x} } dx=\int \frac{cos x}{e^u }\times \frac{du}{cos x} \\ =\int \frac{ 1}{e^u} du \\ =\int e^{-u}du \\ =-e^{-u}+C \\ =- e^{-\sin x}+C \\ =-\frac{1}{e^{sin x}}+C \end{gathered}$$

---

                        $$\begin{gathered} 13) \int e^x {(2+ e^x)}^5 dx \\ \hspace{0.17em} \\ 2+e^x=u \Rightarrow e^x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{e^x} \\ \therefore \int e^x {(2+ e^x)}^5 dx=\int e^x {\left(u\right)}^5 \frac{du}{e^x} \\ =\int u^5 du \\ =\frac{1}{6}{u}^6+C \\ =\frac{1}{6}{\left(2+e^x\right)}^6+C \end{gathered}$$

---

 

                  $$\begin{gathered} 14) \int \frac{cos \left(ln\mathit{ }x\right)}{x } dx \\ \hspace{0.17em} \\ ln x=u \Rightarrow \frac{1}{x} = \frac{du}{dx} \\ \Rightarrow dx = x du \\ \therefore \int \frac{cos (ln x)}{x } dx=\int \frac{cos u}{x }\times x du \\ =\int \cos u du \\ =sin u + C \\ =sin \left(ln x\right)+C \end{gathered}$$

---

                 $$\begin{gathered} 15) \int \left(3x^2-2x-1\right){(x^3-x^2-x)}^4 dx \\ \hspace{0.17em} \\ x^3-x^2-x=u \Rightarrow 3x^2-2x-1 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{3x^2-2x-1} \\ \therefore \int \left(3x^2-2x-1\right){(x^3-x^2-x)}^4 dx=\int \left(3x^2-2x-1\right){\left(u\right)}^4 \frac{du}{3x^2-2x-1} \\ =\int u^4 du \\ =\frac{1}{5}{u}^5+C \\ =\frac{1}{5}{(x^3-x^2-x)}^5+C \end{gathered}$$

---

أجد كلًّا من التكاملات الآتية:

                     $$\begin{gathered} 16) {\int }_0^2\left(2x-1\right)e^{x^2-x} dx \\ x^2-x=u\Rightarrow 2x-1=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{2x-1} \\ x=0\Rightarrow u=0^2-0=0 \\ x=2\Rightarrow u=2^2-2=2 \\ \therefore {\int }_0^{2 }(2x-1)e^{x^2-x} dx ={\int }_0^2 (2x-1)e^u\frac{du}{2x-1} \\ ={\int }_0^2 e^u du \\ = e^{u }\overline{)\begin{array}{c}2\\ 0\end{array}} \\ =(e^2-e^0) \\ =e^2-1 \end{gathered}$$

---

                       $$\begin{gathered} 17) {\int }_1^{2 }\frac{e^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$x$}\right.}}{x^2} dx \\ \frac{1}{x}=u\Rightarrow -\frac{1}{x^2}=\frac{du}{dx} \\ \Rightarrow dx=-x^2 du \\ x=1 \Rightarrow u=1 \\ x=2 \Rightarrow u=\frac{1}{2} \\ \therefore {\int }_1^{\frac{1}{2} }\frac{e^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$x$}\right.}}{x^2} dx ={\int }_1^{\frac{1}{2}}\frac{e^u}{x^2} (-x^2 du) \\ =-{\int }_1^{\frac{1}{2}}{e}^u du \\ ={\int }_{\frac{1}{2}}^1{e}^u du=e^u\overline{)\begin{array}{c}1\\ \frac{1}{2}\end{array}} \\ =e^1 -e^{\frac{1}{2}} \\ =e-\sqrt{e} \end{gathered}$$

---

                     $$\begin{gathered} 18) {\int }_e^{e^3} \frac{\sqrt{\ln x}}{x} dx \\ \ln x=u\Rightarrow \frac{1}{x}=\frac{du}{dx} \\ \Rightarrow dx=x du \\ x=e \Rightarrow u=\ln e=1 \\ x=e^3 \Rightarrow u=\ln e^3=3 \\ \therefore {\int }_e^{e^3 }\frac{\sqrt{\ln x}}{x} dx ={\int }_1^3\frac{\sqrt{u}}{x} (x du) \\ ={\int }_1^3\sqrt{u} du \\ ={\int }_1^3{u}^{\frac{1}{2}} du=\frac{2}{3} u^{\frac{3}{2}}\overline{)\begin{array}{c}3\\ 1\end{array} } \\ =\frac{2}{3}\sqrt{u^3}\overline{)\begin{array}{c}3\\ 1\end{array} } \\ =\frac{2}{3}\left(\sqrt{3^3}-\sqrt{1^3}\right) \\ =\frac{2}{3}\left(3\sqrt{3}-1\right) \\ =2\sqrt{3}-\frac{2}{3} \end{gathered}$$

---

                      $$\begin{gathered} 19) {\int }_0^1 \left(x^3+x\right)\sqrt{x^4+2x^2+1} dx \\ x^4+2x^2+1=u\Rightarrow 4x^3+4x=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{4x^3+4x} \\ x=0 \Rightarrow u=0^3+2{\left(0\right)}^2+1=1 \\ x=1\Rightarrow u=1^3+2{\left(1\right)}^2+1=4 \\ \therefore {\int }_0^{1 }(x^3+x)\sqrt{x^4+2x^2+1} dx ={\int }_1^4 (x^3+x)\sqrt{u}\frac{du}{4x^3+4x} \\ ={\int }_1^4(x^3+x)\sqrt{u}\frac{du}{4\left(x^3+x\right)} \\ =\frac{1}{4}{\int }_1^4\sqrt{u }du \\ =\frac{1}{4}{\int }_1^4 u^{\frac{1}{2}} du \\ =\frac{1}{4} \left(\frac{2}{3}{u}^{\frac{3}{2} }\right)\overline{)\begin{array}{c}4\\ 1\end{array} } \\ =\frac{1}{6}\sqrt{u^3}\overline{)\begin{array}{c}4\\ 1\end{array} } \\ =\frac{1}{6}(\sqrt{4^3} -\sqrt{1^3}) \\ =\frac{1}{6}(\sqrt{64} -\sqrt{1}) \\ =\frac{1}{6}\left(8-1\right) \\ =\frac{1}{6}\left(7\right)=\frac{7}{6} \end{gathered}$$

---

                      $$\begin{gathered} 20) {\int }_0^3 \frac{x}{\sqrt{x^2+1}} dx \\ x^2+1=u\Rightarrow 2x=\frac{du}{dx} \\ \Rightarrow dx= \frac{du}{2x} \\ x=0 \Rightarrow u=0^2+1=1 \\ x=3 \Rightarrow u=3^2+1=10 \\ \therefore {\int }_0^{3 }\frac{x}{\sqrt{x^2+1}} dx ={\int }_1^{10 }\frac{x}{\sqrt{u}} \left(\frac{du}{2x}\right) \\ =\frac{1}{2}{\int }_1^{10 }\frac{1}{\sqrt{u}} du \\ =\frac{1}{2}{\int }_1^{10} u^{-\frac{1}{2}} du \\ =\frac{1}{2}\left(2 u^{\frac{1}{2}}\right)\overline{)\begin{array}{c}10\\ 1\end{array}} \\ =\sqrt{u} \overline{)\begin{array}{c}10\\ 1\end{array}} \\ =\sqrt{10}-\sqrt{1} \\ =\sqrt{10}-1 \end{gathered}$$

---

                     $$\begin{gathered} 21) {\int }_1^2 \frac{2x+1}{{\left(x^2+x+4\right)}^3} dx \\ x^2+x+4=u\Rightarrow 2x+1=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{2x+1} \\ x=1 \Rightarrow u=1^2+1+4=6 \\ x=2 \Rightarrow u=2^2+2+4=10 \\ \therefore {\int }_1^{2 }\frac{2x+1}{{(x^2+x+4)}^3} dx ={\int }_6^{10}\frac{2x+1}{{\left(u\right)}^3}\times \frac{du}{2x+1} \\ ={\int }_6^{10}\frac{1}{u^3} du \\ ={\int }_6^{10 }{u}^{-3} du=-\frac{1}{2}\left(u^{-2}\right)\overline{)\begin{array}{c}10\\ 6\end{array}} \\ =-\frac{1}{2}\left(\frac{1}{u^2}\right)\overline{)\begin{array}{c}10\\ 6\end{array}}=-\frac{1}{2}(\frac{1}{{10}^2}-\frac{1}{6^2}) \\ =-\frac{1}{2}(\frac{1}{100}-\frac{1}{36})=-\frac{1}{200}+\frac{1}{72} \\ =-\frac{72}{14400}+\frac{200}{14400}=\frac{128}{14400} \\ =\frac{128÷16}{14400÷16}=\frac{8÷4}{900÷4} \\ =\frac{2}{225} \end{gathered}$$

---

    أجد مساحة المنطقة المظللة في كل من التمثيلين البيانيين الآتيين:     

   

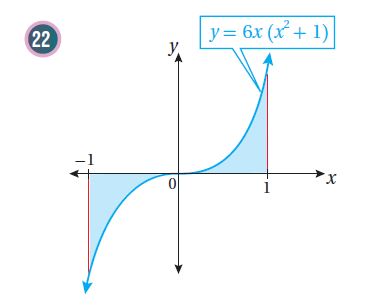
الحل:

 

$A=-{\int }_{-1}^{0}6x\left(x^2+1\right) dx +{\int }_0^{1}6x\left(x^2+1\right) dx$

هناك طريقتان للحل:

1) استخدام التكامل بالتعويض.

2)تكامل كثير الحدود بعد توزيع الأقواس.

 

* طريقة تكامل كثير الحدود:

باستخدام الخاصية التوزيعية                   $A=-{\int }_{-1}^0\left(6x^3+6x\right) dx +{\int }_0^1(6x^3+6x) dx$

تكامل كثير الحدود المضروب بثابت          $=-\left(\frac{6}{4}{x}^4+\frac{6}{2}{x}^2\right)\overline{)\begin{array}{c}0\\ -1\end{array}+} \left(\frac{6}{4}{x}^4+\frac{6}{2}{x}^2\right)\overline{)\begin{array}{c}1\\ 0\end{array}}$

بالتبسيط                                                        $=-\left(\frac{3}{2}{x}^4+3x^2\right)\overline{)\begin{array}{c}0\\ -1\end{array}+} \left(\frac{3}{2}{x}^4+3x^2\right)\overline{)\begin{array}{c}1\\ 0\end{array}}$

بالتعويض                            $=-\left(0-\left(\frac{3}{2}{\left(-1\right)}^4+3{\left(-1\right)}^2\right)\right)+ \left(\frac{3}{2}{\left(1\right)}^4+3{\left(1\right)}^2-0\right)$

بالتبسيط                                                                                                 $$\begin{gathered} =\left(\frac{3}{2}+3\right)+ \left(\frac{3}{2}+3\right) \\ =\frac{6}{2}+6 \\ =3+6 \\ =9 \end{gathered}$$

إذن مساحة المنطقة المظللة هي 9 وحدات مربعة.

---

 

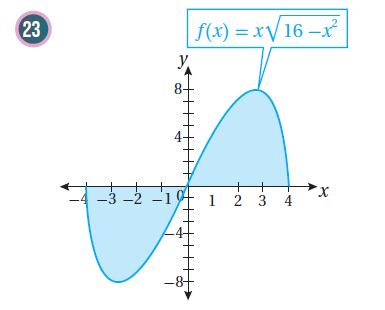
الحل:

$A=-{\int }_{-4}^{0}x\sqrt{16-x^2} dx +{\int }_0^{4}x\sqrt{16-x^2} dx$

* باستخدام طريقة التكامل بالتعويض:

افترض أنّ:$16-x^2=u$                        $$\begin{gathered} 16-x^2=u\Rightarrow -2x=\frac{du}{dx} \\ \Rightarrow dx=-\frac{du}{2x} \end{gathered}$$

 

بإيجاد الحدين العلوي والسفلي            $$\begin{gathered} x=-4 \Rightarrow u=16-{\left(-4\right)}^2=0 \\ x=0 \Rightarrow u=16-{\left(0\right)}^2=16 \\ x=4 \Rightarrow u=16-{\left(4\right)}^2=0 \end{gathered}$$

 

بالتعويض بالتكامل الأصلي                 $A=-{\int }_0^{16} x\sqrt{u} \left(-\frac{du}{2x}\right) +{\int }_{16}^{0}x\sqrt{u} \left(-\frac{du}{2x}\right)$

بالتبسيط واستخدام الصورة الأسية                             $=\frac{1}{2}{\int }_0^{16} u^{\frac{1}{2}} du -\frac{1}{2}{\int }_{16}^0{u}^{\frac{1}{2}} du$ 

باستخدام قوانين التكامل                                            $$\begin{gathered} =\frac{1}{2}{\int }_0^{16} u^{\frac{1}{2}} du +\frac{1}{2}{\int }_0^{16}{u}^{\frac{1}{2}} du \\ ={\int }_0^{16} u^{\frac{1}{2}} du \end{gathered}$$            

تكامل اقتران القوة المضروب بثابت                                                                      $=\frac{2}{3} u^{\frac{3}{2}} \overline{)\begin{array}{c}16\\ 0\end{array}}$

بالتعويض، الصورة الجذرية                                                                       $=\frac{2}{3}\left(\sqrt{{16}^3}-\sqrt{0^3}\right)$  

بالتبسيط                                                                                                                                                                                        $=\frac{2}{3}\left(64\right)=\frac{128}{3}$  

إذن مساحة المنطقة المظللة هي $\frac{128}{3}$ وحدة مربعة.

---

في كل مما يأتي المشتقة الأولى للاقتران $f\left(x\right)$، ونقطة يمر بها منحنى $y=f\left(x\right)$.

أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f\left(x\right)$:

 

$24) f \mathit{َ}\mathbf{ }(x)=x e^{4-x^2} , (-2 , 1)$

الحل:

الخطوة الأولى:أجد تكامل المشتقة الأولى باستخدام طريقة التعويض:

                           $$\begin{gathered} f\left(x\right)=\int x e^{4-x^2} dx \\ u = 4-x^{2 }\Rightarrow \frac{du}{dx}=-2x \\ \Rightarrow -\frac{du}{2x}= dx \\ \therefore \int x e^{4-x^2} dx =\int x e^u (-\frac{du}{2x}) \\ =-\frac{1}{2}\int e^u du \\ =-\frac{1}{2}{e}^u +C \\ =-\frac{1}{2}{e}^{4-x^2} +C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $\left(-2, 1\right)$:

                          $$\begin{gathered} f(-2)=-\frac{1}{2}{e}^{4-{\left(-2\right)}^2} +C \\ 1 =-\frac{1}{2}{e}^{4-4} +C \\ 1=-\frac{1}{2}+C \\ \Rightarrow C=1+\frac{1}{2}=\frac{3}{2} \end{gathered}$$       

الخطوة الثالثة :أكتب قاعدة الاقتران $f\left(x\right)$:

                           $f\left(x\right)=-\frac{1}{2}{e}^{4-x^2} +\frac{3}{2}$

---

$25) f \mathit{َ}\mathbf{ }(x)=\frac{2x}{{\left(1-x^2\right)}^2} ; \left(0 , -1\right)$

 

الحل:

الخطوة الأولى:أجد تكامل المشتقة الأولى باستخدام طريقة التعويض:

                          $$\begin{gathered} f\left(x\right)=\int \frac{2x}{{\left(1-x^2\right)}^2} dx \\ u = 1-x^{2 }\Rightarrow \frac{du}{dx}=-2x \\ \Rightarrow -\frac{du}{2x}= dx \\ \therefore \int \frac{2x}{{\left(1-x^2\right)}^2} dx =\int \frac{2x}{u^2} (-\frac{du}{2x}) \\ =-\int \frac{1}{u^2} du \\ =-\int u^{-2} du \\ =-\left(-u^{-1}\right)+C \\ =\frac{1}{u} +C \\ = \frac{1}{1-x^2}+C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $\left(0 , -1\right)$:

                            $$\begin{gathered} f\left(0\right)= \frac{1}{1-{\left(0\right)}^2}+C \\ -1 =1+C \\ \Rightarrow C=-1-1=-2 \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $f\left(x\right)$:

                                                           $f\left(x\right)= \frac{1}{1-x^2}-2$

---

26) يتحرك جسيم في مسار مستقيم، وتُعطى سرعته المتجهة بالاقتران:$v\left(t\right)=\frac{-2t}{\sqrt{{\left(1+t^2\right)}^3}}$،

      حيث $t$ الزمن بالثواني، و $v$ سرعته المتجهة بالمتر لكل ثانية.

      إذا كان الموقع الابتدائي للجسيم $4 m$ فأجد موقع الجسيم بعد $t$ ثانية من بدء الحركة.

 

الحل:

الخطوة الأولى: أجد اقتران الموقع $s\left(t\right)$

بإيجاد تكامل اقتران السرعة المتجهة                                 $s\left(t\right) = \int v\left(t\right) dt$

 

 بتعويض     $v\left(t\right)=\frac{-2t}{\sqrt{{(1+t^2)}^3}}$                                      $=\int \frac{-2t}{\sqrt{{(1+t^2)}^3}}dt$

 

استخدام طريقة التعويض لإيجاد التكامل           $$\begin{gathered} u = 1+t^{2 }\Rightarrow \frac{du}{dt}=2t \\ \Rightarrow \frac{du}{2t}= dt \end{gathered}$$   

                                                                                             

                                                              $$\begin{gathered} \therefore \int \frac{-2t}{\sqrt{{\left(1+t^2\right)}^3}} dt =\int \frac{-2t}{\sqrt{u^3}} \left(\frac{du}{2t}\right) \\ =-\int \frac{1}{\sqrt{u^3}} du \\ =-\int u^{-\frac{3}{2}} du \\ =-(-2u^{-\frac{1}{2}})+C \\ =\frac{2}{\sqrt{u}} +C \\ =\frac{2}{\sqrt{1+t^2}}+C \end{gathered}$$                

 

 

الخطوة الثانية: أجد قيمة ثابت التكامل $C$:

اقتران الموقع                                  $s\left(t\right)=\frac{2}{\sqrt{1+t^2}}+C$

 

الموقع الابتدائي يعني $s\left(0\right)$           $s\left(0\right)=\frac{2}{\sqrt{1+{\left(0\right)}^2}}+C$

بتعويض $t=0 , s\left(0\right)=4$                     $4=\frac{2}{\sqrt{1+0}}+C$

بحل المعادلة                                        $$\begin{gathered} 4=2+C \\ \Rightarrow C=4-2=2 \end{gathered}$$

 

الخطوة الثالثة: أكتب اقتران الموقع $s\left(t\right)$

اقتران الموقع بعد t ثانية من بدء الحركة هو: $s\left(t\right)=\frac{2}{\sqrt{1+t^2}}+2$

---

27)زراعة: يمثل الاقتران $V\left(t\right)$ سعر دونم أرض زراعية في الأغوار الأردنية (بالدينار) بعد t سنة من الآن.

                 إذا كان:$V \mathit{َ}\mathbf{ }\left(t\right)=\frac{0.4 t^3}{\sqrt[3]{0.2 t^4+8000}}$ هو معدل التغير في سعر دونم الأرض،

                فأجد $V\left(t\right)$ ، علمًا بأن سعره الآن $JD 5000$.

الحل:

الخطوة الأولى: أجد الاقتران $V\left(t\right)$، بإيجاد تكامل المشتقة :

                                         $$\begin{gathered} V\left(t\right)=\int \frac{0.4 t^3}{\sqrt[3]{0.2 t^4+8000}} dt \\ u=0.2 t^4 + 8000 \Rightarrow \frac{du}{dt}=0.8 t^{3 } \\ \Rightarrow \frac{du}{0.8 t^3}=dt \\ \therefore \int \frac{0.4 t^3}{\sqrt[3]{0.2 t^4+8000}} dt=\int \frac{0.4 t^3}{\sqrt[3]{u}}\times \frac{du}{0.8 t^3} \\ =\frac{0.4}{0.8}\int \frac{1}{\sqrt[3]{u}}du \\ =\frac{1}{2}\int u^{-\frac{1}{3}} du \\ =\frac{1}{2}\left(\frac{3}{2}{u}^{\frac{2}{3}}\right)+C \\ =\frac{3}{4}\sqrt[3]{u^2} +C \\ =\frac{3}{4} \sqrt[3]{{\left(0.2 t^4+8000\right)}^2} +C \end{gathered}$$

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $\left(0 , 5000\right)$:

                                            $$\begin{gathered} P\left(0\right)=\frac{3}{4} \sqrt[3]{{(0.2 t^4+8000)}^2} +C \\ 5000=\frac{3}{4} \sqrt[3]{({8000)}^2} +C \\ 5000=\frac{3}{4}{\left(\sqrt[3]{8000}\right)}^2+C \\ 5000=\frac{3}{4}{\left(20\right)}^2+C \\ 5000=\frac{3}{4}\left(400\right)+C \\ 5000=300+C \\ \Rightarrow C=5000-300=4700 \end{gathered}$$

الخطوة الثالثة :أكتب قاعدة الاقتران $V\left(t\right)$

                                                                                                                           $V\left(t\right)=\frac{3}{4} \sqrt[3]{{(0.2 t^4+8000)}^2} +4700$

---

28)سكان: أشارت دراسة إلى أنّ عدد السكان في إحدى المدن يتغير سنويًا بمعدل

     يمكن نمذجته بالاقتران:$P \mathit{َ}\mathbf{ }\left(t\right)=\frac{4 e^{0.2t}}{\sqrt{4+e^{0.2t}}}$ ، حيث t عدد السنوات منذ عام $2015$ م،

     وَ $P\left(t\right)$ عدد السكان بالآلاف.

     أجد مقدار الزيادة في عدد سكان المدينة من عام 2015 م إلى عام 2025م.

الحل:

أجد تكامل المشتقة باستخدام  طريقة التعويض:

                                                                                                                 $$\begin{gathered} P\left(t\right)={\int }_0^{10}\frac{4 e^{0.2t}}{\sqrt{4+ e^{0.2t}}} dt \\ u=4+e^{0.2 t} \Rightarrow \frac{du}{dt}=0.2 e^{0.2t } \\ \Rightarrow \frac{ du}{0.2 e^{0.2t}}=dt \\ t=0 \Rightarrow u=4+e^{0.2\left(0\right)} =4+1=5 \\ t=10\Rightarrow u=4+e^{0.2\left(10\right)} =4+e^2 \\ \therefore {\int }_0^{10}\frac{4 e^{0.2t}}{\sqrt{4+ e^{0.2t}}} dt={\int }_5^{4+e^2} \frac{4 e^{0.2t}}{\sqrt{u}}\times \frac{du}{0.2 e^{0.2t}} \\ =\frac{4}{0.2}{\int }_5^{4+e^2} \frac{1}{\sqrt{u}}du \\ =20 {\int }_5^{4+e^2} u^{-\frac{1}{2}} du \\ =20 (2 u^{\frac{1}{2}})\overline{)\begin{array}{c}4+e^2\\ 5\end{array}} \\ =40\left(\sqrt{u}\right) \overline{)\begin{array}{c}4+e^2\\ 5\end{array}} \\ =40\left(\sqrt{4+e^2} -\sqrt{5}\right) \\ =40\left(\sqrt{4+e^2}\right) -40\sqrt{5} \\ \approx 135 -89=46 \end{gathered}$$

إذن يزداد عدد سكان المدينة من عام 2015 م إلى عام 2025م بحوالي: 46 ألف شخص تقريبًا

---

مهارات التفكير العليا:

29) أكتشف المختلف: أي التكاملات الآتية مختلف ، مبررًا إجابتي؟

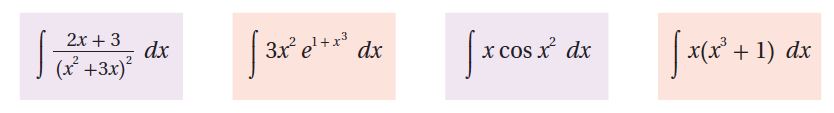
الحل:

التكامل المختلف هو: $\int x\left(x^3+1\right) dx$؛ لأنه الوحيد الذي لا يمكن حله بطريقة التكامل بالتعويض.

---

30) أكتشف الخطأ: أوجدت سعاد ناتج التكامل:${\int }_0^1 8x {(x^2+1)}^3 dx$ ، وكان حلها على النحو الآتي:

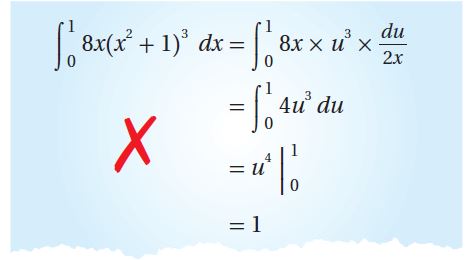
أكتشف الخطأ في حل سعاد، ثم أصححه.

 

الخطأ: لم تقم سعاد بتغيير حدود التكامل بعد أن فرضت أن $u=x^2+1$.

التصحيح:

                 $$\begin{gathered} u =x^2+1 \Rightarrow \frac{du}{dx}=2x \\ \Rightarrow \frac{du}{2x}=dx \\ x=0 \Rightarrow u={\left(0\right)}^2+1=1 \\ x=1 \Rightarrow u={\left(1\right)}^2+1=2 \\ \therefore {\int }_0^1 8x {(x^2+1)}^3 dx ={\int }_1^2 8x {\left(u\right)}^3 \frac{du}{2x} \\ ={\int }_1^2 \frac{8x}{2x} {\left(u\right)}^3 du \\ =4 {\int }_1^2 u^3 du \\ =4 \left(\frac{u^4}{4}\right) \overline{)\begin{array}{c}2\\ 1\end{array} } \\ = u^{4 }\overline{)\begin{array}{c}2\\ 1\end{array} } \\ =2^4-1^4 = 16-1=15 \end{gathered}$$

---

31) تحدٍّ: إذا كان: ${\int }_0^{k}k x^2 e^{x^3} dx = \frac{2}{3}\left(e^8-1\right)$ ، فأجد قيمة الثابت $k$ .

الحل:

                                                        $$\begin{gathered} u =x^3 \Rightarrow \frac{du}{dx}=3x^2 \\ \Rightarrow \frac{du}{3x^2}=dx \\ x=0 \Rightarrow u={\left(0\right)}^3=0 \\ x=k \Rightarrow u={\left(k\right)}^3=k^3 \\ \therefore {\int }_0^k k x^2 e^{x^3} dx ={\int }_0^{k^3} k x^2 e^u \frac{du}{3x^2} \\ ={\int }_0^{k^3} \frac{k x^2}{3 x^2} e^u du \\ =\frac{k}{3} {\int }_0^{k^3} e^u du \\ =\frac{k}{3} e^u \overline{)\begin{array}{c}{k}^3\\ 0\end{array} } \\ =\frac{k}{3}\left(e^{k^3}-e^0\right) = \frac{k}{3}\left(e^{k^3}-1\right) \\ \because {\int }_0^k k x^2 e^{x^3} dx = \frac{2}{3}\left(e^8-1\right) \\ \Rightarrow \frac{k}{3}\left(e^{k^3}-1\right) =\frac{2}{3}\left(e^8-1\right) \\ \therefore k = 2 \end{gathered}$$

---

كتاب التمارين صفحة 14:

أجد كلًا من التكاملات الآتية:

                                                              $$\begin{gathered} 1) \int x \sqrt{x^2+3} dx \\ \hspace{0.17em} \\ x^2+3=u \Rightarrow 2x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2x} \\ \therefore \int x \sqrt{x^2+3} dx=\int x \sqrt{u} \times \frac{du}{2x} \\ =\frac{1}{2}\int \sqrt{u} du=\frac{1}{2}\int u^{\frac{1}{2}} du \\ =\frac{1}{2}\left(\frac{2}{3}{u}^{\frac{3}{2}}\right)+C \\ =\frac{1}{3}\sqrt{u^3}+C \\ =\frac{1}{3}\sqrt{{\left(x^2+3\right)}^3}+C \end{gathered}$$

---

                                          $$\begin{gathered} 2) \int x^4 e^{x^5+2} dx \\ \hspace{0.17em} \\ x^5+2=u \Rightarrow 5x^4 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{5 x^4} \\ \therefore \int x^4 e^{{}^{x^5+2}} dx=\int x^4 e^u \frac{du}{5 x^4} \\ =\frac{1}{5}\int e^u du \\ =\frac{1}{5}{e}^u+C \\ =\frac{1}{5}{e}^{x^5+2}+C \end{gathered}$$

---

                                         $$\begin{gathered} 3) \int (x+1) {(x^2+2x+5)}^4 dx \\ \hspace{0.17em} \\ x^2+2x+5=u \Rightarrow 2x+2 = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{2x +2} \\ \therefore \int (x+1){(x^2+2x +5)}^4 dx=\int (x+1){\left(u\right)}^4 \frac{du}{2x+2} \\ =\int (x+1){\left(u\right)}^4 \frac{du}{2(x+1)} \\ =\frac{1}{2}\int u^4 du \\ =\frac{1}{2}(\frac{1}{5}{u}^5)+C \\ =\frac{1}{10}{(x^2+2x +5)}^5+C \end{gathered}$$

 

---

                                       $$\begin{gathered} 4) \int \frac{{\left(\ln x\right)}^3}{x} dx \\ \hspace{0.17em} \\ \ln x=u \Rightarrow \frac{1}{x} = \frac{du}{dx} \\ \Rightarrow dx = x du \\ \therefore \int \frac{{(ln x)}^3}{x} dx=\int \frac{u^3}{x}\times x du \\ =\int u^3 du \\ =\frac{u^4}{4}+C \\ =\frac{1}{4}{(ln x)}^4+C \end{gathered}$$

---

                                      $$\begin{gathered} 5) \int \frac{\cos x}{{\sin }^4 x} dx \\ \hspace{0.17em} \\ sin x=u \Rightarrow \cos x = \frac{du}{dx} \\ \Rightarrow dx = \frac{du}{\cos x} \\ \therefore \int \frac{\cos x}{{\sin }^4 x} dx=\int \frac{cos x}{u^4 }\times \frac{du}{cos x} \\ =\int \frac{ 1}{u^4} du \\ =\int u^{-4}du \\ =\frac{u^{-3}}{-3}+C \\ =-\frac{1 }{3 u^3}+C \\ =-\frac{1}{3 {\sin }^{3}x}+C \end{gathered}$$

---

                                $$\begin{gathered} 6) \int \sin x \sqrt{1+ 3\cos x} dx \\ \hspace{0.17em} \\ 1+3\cos x=u \Rightarrow -3\sin x = \frac{du}{dx} \\ \Rightarrow dx = -\frac{du}{3\sin x} \\ \therefore \int \sin x \sqrt{1+3\cos x} dx=\int \sin x \sqrt{u} \times \frac{-du}{3 \sin x} \\ =-\frac{1}{3}\int u^{\frac{1}{2}} du \\ =-\frac{1}{3}\left(\frac{2}{3}{u}^{\frac{3}{2}}\right)+C \\ =-\frac{2}{9}\sqrt{u^3} +C \\ =-\frac{2}{9} \sqrt{{(1+3 \cos x)}^3}+C \end{gathered}$$

---

أجد كلًا من التكاملات الآتية:

                          

                                   $$\begin{gathered} 7) {\int }_1^2 \frac{x^2}{{\left(x^3+1\right)}^2} dx \\ x^3+1=u\Rightarrow 3x^2=\frac{du}{dx} \\ \Rightarrow dx=\frac{du}{3 x^2} \\ x=1 \Rightarrow u=1^3+1=2 \\ x=2 \Rightarrow u=2^3+1=9 \\ \therefore {\int }_1^{2 }\frac{x^2}{{(x^3+1)}^2} dx ={\int }_2^{9 }\frac{x^2}{{\left(u\right)}^2}\times \frac{du}{3 x^2} \\ =\frac{1}{3}{\int }_2^9\frac{1}{u^2} du \\ =\frac{1}{3}{\int }_2^{9 }{u}^{-2} du=\frac{1}{3}(-u^{-1})\overline{)\begin{array}{c}9\\ 2\end{array}} \\ =-\frac{1}{3}\left(\frac{1}{u}\right)\overline{)\begin{array}{c}9\\ 2\end{array}}=-\frac{1}{3}(\frac{1}{9}-\frac{1}{2}) \\ =-\frac{1}{3}(\frac{2}{18}-\frac{9}{18})=-\frac{1}{3}\left(-\frac{7}{18}\right) \\ =\frac{7}{54} \end{gathered}$$

---

                                   

                                  $$\begin{gathered} 8) {\int }_0^1 x \sqrt{3x^2+2} dx \\ u=3x^2+2\Rightarrow \frac{du}{dx}=6x \\ \Rightarrow dx=\frac{du}{6x} \\ x=0 \Rightarrow u = 3\left(0^2\right)+2 =2 \\ x=1 \Rightarrow u = 3\left(1^2\right)+2 =5 \\ \therefore {\int }_0^1 x \sqrt{3x^2+2} dx= {\int }_2^5 x \sqrt{u} \frac{du}{6 x} \\ =\frac{1}{6}{\int }_2^5 \sqrt{u} du \\ =\frac{1}{6}\left(\frac{2}{3}{u}^{\frac{3}{2}}\right) \overline{)\begin{array}{c}5\\ 2\end{array}} \\ =\frac{1}{9}\left(\sqrt{u^3}\right) \overline{)\begin{array}{c}5\\ 2\end{array}} \\ =\frac{1}{9}\left(\sqrt{5^3} -\sqrt{2^3}\right) \\ =\frac{1}{9}\left(\sqrt{125}\right)-\sqrt{8}) \\ =\frac{1}{9}\sqrt{125} -\frac{1}{9}\sqrt{8} \end{gathered}$$

---

                                   $$\begin{gathered} 9) {\int }_e^{e^2} \frac{{\left(\ln x\right)}^2}{x} dx \\ u=ln x \Rightarrow \frac{du}{dx}=\frac{1}{x}\Rightarrow dx = x du \\ x = e \Rightarrow u = \ln e = 1 \\ x = e^2 \Rightarrow u = ln e^2 = 2 \\ \therefore {\int }_e^{e^2} \frac{{(ln x)}^2}{x} dx = {\int }_1^2 \frac{u^2}{x} \times x du \\ = {\int }_1^2 u^2 du \\ =\frac{u^3}{3}\overline{)\begin{array}{c}2\\ 1\end{array}} \\ =\frac{2^3}{3}-\frac{1^3}{3} \\ =\frac{8}{3}-\frac{1}{3}=\frac{7}{3} \end{gathered}$$

---

                                   $$\begin{gathered} 10) {\int }_0^1 \left(x+1\right){\left(x^2+2x\right)}^5 dx \\ u=x^2+2x\Rightarrow \frac{du}{dx}=2x+2 \\ \Rightarrow dx=\frac{du}{2x+2} \\ x=0 \Rightarrow u = \left(0^2\right)+2\left(0\right) =0 \\ x=1 \Rightarrow u = \left(1^2\right)+2\left(1\right) =3 \\ \therefore {\int }_0^1 \left(x+1\right) {\left(x^2+2x\right)}^5 dx= {\int }_0^3 \left(x+1\right) {\left(u\right)}^5\times \frac{du}{2\left(x+1\right)} \\ =\frac{1}{2}{\int }_0^3 u^5 du \\ =\frac{1}{2}\left(\frac{1}{6}{u}^6\right) \overline{)\begin{array}{c}3\\ 0\end{array}} \\ =\frac{1}{12}\left(3^6-0^6\right) \\ =\frac{1}{12}\left(729 -0\right) \\ =\frac{729}{12} \end{gathered}$$

---

11) أجد مساحة المنطقة المظللة في التمثيل البياني الآتي:

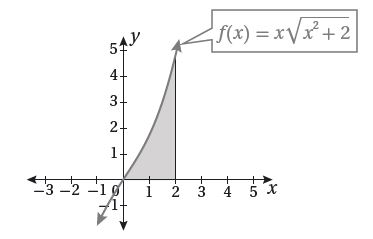
الحل:

$A={\int }_0^{2}x\sqrt{x^2+2} dx$

* باستخدام طريقة التكامل بالتعويض:

افترض أنّ:$u=x^2+2$                                        $$\begin{gathered} u = x^2+2 \Rightarrow \frac{du}{dx} = 2x \\ \Rightarrow dx =\frac{du}{2x} \end{gathered}$$

بإيجاد الحدين العلوي والسفلي                           $$\begin{gathered} x=0 \Rightarrow u={\left(0\right)}^2+2=2 \\ x=2 \Rightarrow u={\left(2\right)}^2+2=6 \end{gathered}$$

بالتعويض بالتكامل الأصلي والتبسيط 

                           $$\begin{gathered} {\int }_0^2 x\sqrt{x^2+2} dx={\int }_2^{6}x \sqrt{u} \times \frac{du}{2x} \\ =\frac{1}{2}{\int }_2^6 \sqrt{u} du \end{gathered}$$

تكامل اقتران القوة المضروب بثابت             $=\frac{1}{2}\left(\frac{2}{3}{u}^{\frac{3}{2}}\right) \overline{)\begin{array}{c}6\\ 2\end{array} }=\frac{1}{3}\sqrt{u^3} \overline{)\begin{array}{c}6\\ 2\end{array} }$

بالتعويض والتبسيط                                                         $$\begin{gathered} =\frac{1}{3}\left(\sqrt{6^3}-\sqrt{2^3}\right) \\ =\frac{1}{3}\sqrt{216} -\frac{1}{3}\sqrt{8} \end{gathered}$$

---

11) الإيراد الحدي: يمثل الاقتران: $R \mathit{َ}\mathbf{ }\left(x\right)=50 + 3.5 x e^{-0.1 x^2}$ الإيراد الحدي (بالدينار)

                          لكل قطعة تباع من إنتاج إحدى الشركات، حيث $x$ عدد القطع المبيعة،

                          وَ $R\left(x\right)$ إيراد بيع $x$ قطعة بالدينار.

                          أجد اقتران الإيراد $R\left(x\right)$، علمًا بأن $R\left(0\right)=0$ .

الحل:

الخطوة الأولى: أجد الاقتران $R\left(x\right)$ بإيجاد تكامل مشتقته:

                          $$\begin{gathered} R\left(x\right)=\int \left(50 + 3.5 x e^{-0.1 x^2}\right) dx \\ u=-0.1 x^2 \Rightarrow \frac{du}{dx}=-0.2 x \\ \Rightarrow -\frac{du}{0.2 x}=dx \\ \therefore \int (50 + 3.5 x e^{-0.1 x^2}) dx=\int 50 dx +3.5\int x e^u \times -\frac{du}{0.2 x} \\ =50 x -\frac{3.5}{0.2}\int e^u du \\ =50 x -17.5 e^u +C \\ =50 x -17.5 e^{-0.1 x^2} +C \\ \therefore R\left(x\right)=50 x -17.5 e^{-0.1 x^2} +C \end{gathered}$$

 

الخطوة الثانية :أجد ثابت التكامل C ، بتعويض النقطة $\left(0 , 0\right)$

                                                           $$\begin{gathered} R\left(0\right)=50 \left(0\right) -17.5 e^{-0.1 {\left(0\right)}^2} +C \\ 0 = 0 - 17.5 e^0 +C \\ 0=-17.5 + C \\ \Rightarrow C=17.5 \end{gathered}$$

 

الخطوة الثالثة :أكتب قاعدة الاقتران $R\left(x\right)$

                           $R\left(x\right)=50 x -17.5 e^{-0.1 x^2} +17.5$

---

يمثل الاقتران $f \mathit{َ}\mathbf{ }\left(x\right)$ في كل مما يأتي ميل المماس لمنحنى الاقتران $f\left(x\right)$ المار بالنقطة المعطاة.

أستعمل المعلومات المعطاة لإيجاد قاعدة الاقتران $f\left(x\right)$:

                    $$\begin{gathered} 13) f \mathit{َ} (x) =2x {(4x^2-10)}^2 ; (2, 10) \\ u=4x^2-10 \Rightarrow \frac{du}{dx}=8x \\ \Rightarrow dx=\frac{du}{8x} \\ \therefore \int 2x {(4x^2-10)}^2 dx =\int 2x \left(u^2\right) \times \frac{du}{8x} \\ =\frac{2}{8}\int u^2 du \\ =\frac{1}{4}\left(\frac{u^3}{3}\right)+C \\ =\frac{1}{12}{(4x^2-10)}^3+C \Rightarrow f\left(2\right)=\frac{1}{12}{(4{\left(2\right)}^2-10)}^3+C \\ 10 =\frac{1}{12}{(16-10)}^3+C\Rightarrow 10=\frac{216}{12}+C \\ 10=18+C \\ \Rightarrow C=-8 \\ \therefore f\left(x\right)=\frac{1}{12}{(4x^2-10)}^3-8 \end{gathered}$$

---

                $$\begin{gathered} 14) f \mathit{َ} (x) =x^2 e^{-0.2 x^3} ; (0, \frac{3}{2}) \\ u=-0.2 x^3 \Rightarrow \frac{du}{dx}=-0.2\left(3x^2\right) \\ \Rightarrow dx=-\frac{du}{0.6 x^2} \\ \therefore \int x^2 e^{-0.2 x^3} dx =\int x^2 e^u \times \left(-\frac{du}{0.6 x^2}\right) \\ =-\frac{1}{0.6}\int e^u du \\ =-\frac{10}{6}{e}^u+C \\ =-\frac{5}{3}{e}^{-0.2 x^3}+C \\ \Rightarrow f\left(0\right)=-\frac{5}{3}{e}^{-0.2 {\left(0\right)}^3}+C \\ \frac{3}{2}=-\frac{5}{3}+C \\ \frac{3}{2}+\frac{5}{3}=C \\ \Rightarrow C=\frac{19}{6} \\ \therefore f\left(x\right)=-\frac{5}{3}{e}^{-0.2 x^3}+\frac{19}{6} \end{gathered}$$

---

15)  يتحرك جسيم في مسار مستقيم، وتُعطى سرعته المتجهة بالاقتران: $v\left(t\right)=\frac{t}{\sqrt{t^2+1}}$،

       حيث $t$ الزمن بالثواني، وَ $v$ سرعته المتجهة بالمتر لكل ثانية.

       إذا بدأ الجسيم حركته من نقطة الأصل فجد موقعه بعد $t$ ثانية من بدء الحركة.

الحل:

الخطوة الأولى: أجد اقتران الموقع $s\left(t\right)$

بإيجاد تكامل اقتران السرعة المتجهة                         $s\left(t\right) = \int v\left(t\right) dt$

بتعويض $v\left(t\right)=\frac{t}{\sqrt{t^2+1}}$                                     $=\int \frac{t}{\sqrt{t^2+1}}dt$        

  استخدام طريقة التعويض لإيجاد التكامل        $$\begin{gathered} u = t^{2 }+1\Rightarrow \frac{du}{dt}=2t \\ \Rightarrow \frac{du}{2t}= dt \end{gathered}$$

                                                                          $$\begin{gathered} \therefore \int \frac{t}{\sqrt{t^2+1}} dt =\int \frac{t}{\sqrt{u}} \left(\frac{du}{2t}\right) \\ =\frac{1}{2}\int \frac{1}{\sqrt{u}} du \\ =\frac{1}{2}\int u^{-\frac{1}{2}} du \\ =\frac{1}{2}\left(2u^{\frac{1}{2}}\right)+C \\ =\sqrt{u} +C \\ =\sqrt{t^2+1}+C \end{gathered}$$

الخطوة الثانية: أجد قيمة ثابت التكامل $C$:

اقتران الموقع                                                                     $s\left(t\right)=\sqrt{t^2+1}+C$

الموقع الابتدائي يعني$s\left(0\right)=0$                         $$\begin{gathered} s\left(0\right)=\sqrt{{\left(0\right)}^2+1} +C \\ 0 =1+C \\ \Rightarrow C=-1 \end{gathered}$$

الخطوة الثالثة: أكتب اقتران الموقع $s\left(t\right)$

إذن موقع الجسيم بعد $t$ ثانية من بدء الحركة هو: $s\left(t\right)=\sqrt{t^2+1}-1$

---

انتهت الأسئلة