مفهوم أساسي:
التكبير (Enlargement):تحويلٌ هندسيٌّ تزيدُ فيهِ أبعادُ الشكلِ الأصليِّ بِنسبةٍ ثابتةٍ،وَيُسمّى الشكلُ الجديدُ صورةً.وَصورةُ الشكلِ تحتَ تأثيرِ التكبيرِ مشابهةٌ لِلشكلِ الأصليِّ، ما يعني أنَّ أطوالَ الأضلاعِ المتناظرةِ متناسبةٌ، وَالزوايا المتناظرةَ متطابقةٌ.
مُعاملَ التكبيرِ (Scale factor):النسبةُ بينَ طولِ ضلعِ الصورةِ وَطولِ الضلعِ المناظِرِ لَهُ في الشكلِ الأصليِّ وَقيمتُهُ k و يدلُّ على عددِ مراتِ تكبيرِ الصورةِ.
مركزُ التكبيرِ (Center of enlargement) :فَهُوَ النقطةُ الثابتةُ الّتي يُكَبَّر منها الشكلُ.
يمكنُ رسمُ صورةِ شكلٍ تحتَ تأثيرِ تكبيرٍ بِاستعمالِ شبكةِ المربَّعاتِ.
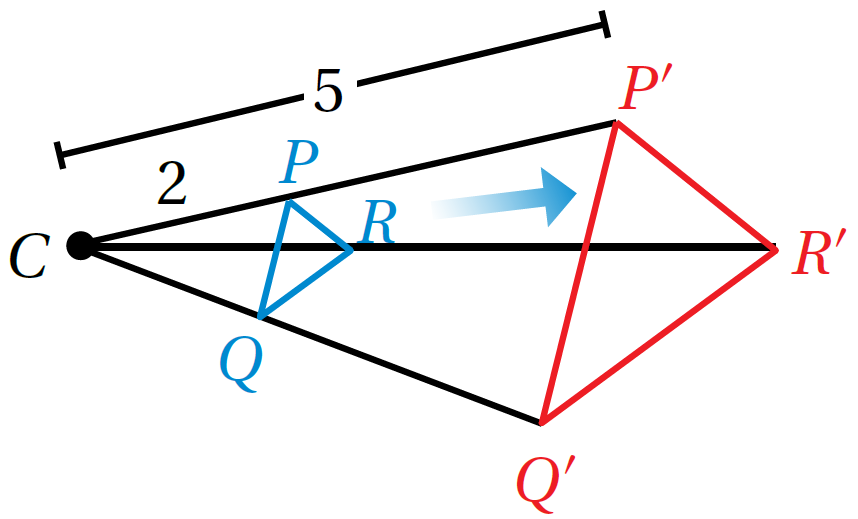
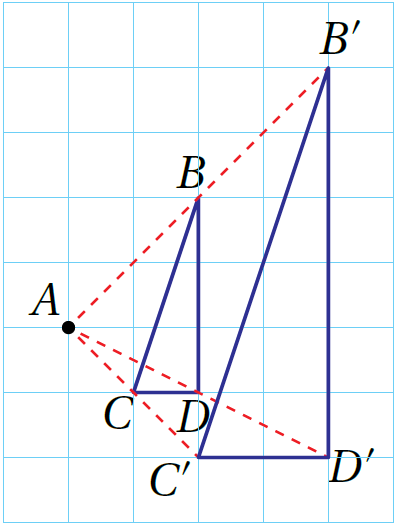
مثال 1:أرسمُ صورةَ ΔCBD تحتَ تأثيرِ تكبيرٍ مركزُهُ النقطةُ A ومعامله 2
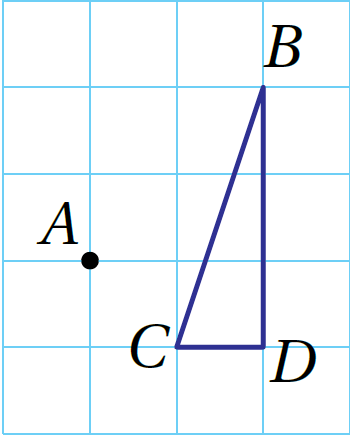
الْخُطْوَةُ 1:أبدأُ بِرسمِ خطوطٍ بِاستعمالِ المسطرةِ ابتداءً مِنْ مركزِ التكبيرِ بِحيثُ يمرُّ كلٌّ منها بأحدِ رؤوسِ المثلثِ، وَأَمدُّ الخطوطَ على استقامتِها.
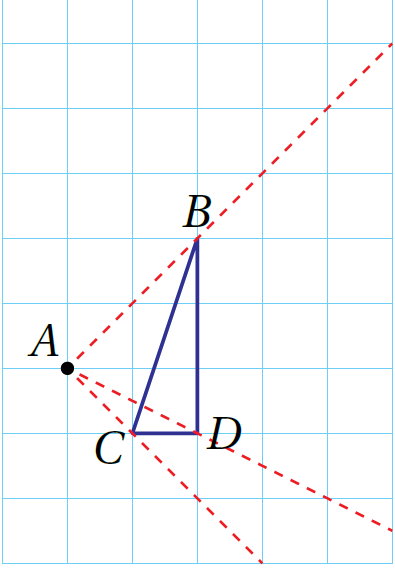
الْخُطْوَةُ 2: أقيسُ المسافةَ بينَ مركزِ التكبيرِ وَكلِّ رأسٍ مِنْ رؤوسِ المثلثِ بِاستعمالِ المسطرةِ، ثمَّ أضربُ القياساتِ الّتي حصلْتُ عليها في 2 (معامل التكبير)
الْخُطْوَةُ 3: أقيسُ المسافاتِ الجديدةَ على الخطوطِ الّتي رسمْتُها في الخطوةِ 1 ابتداءً مِنْ مركزِ التكبيرِ، وَأحدّدُ علامةً لِكلٍّ مِنها.
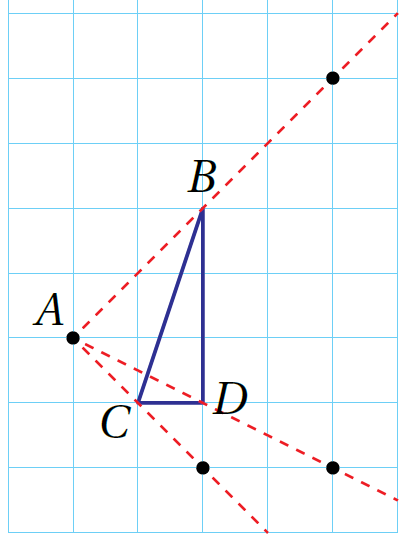
الْخُطْوَةُ 4: أَصِلُ بينَ النقاطِ، وَأسمّي المثلثَ 'B'C'D الجديدَ
يمكن أيضًا استعمالُ إحداثياتِ رؤوسِ الشكلِ لِرسمِ صورتِهِ في المستوى الإحداثيِّ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ ومعامله k
لِايجادِ صورةِ شكلٍ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ ومعامله k أضربُ إحداثيَّيْ كلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في مُعامِلِ التكبيرِ k حيث k>1 وَذلكَ لِاحصلَ على إحداثياتِ رؤوسِ الصورةِ.
مثال 2:
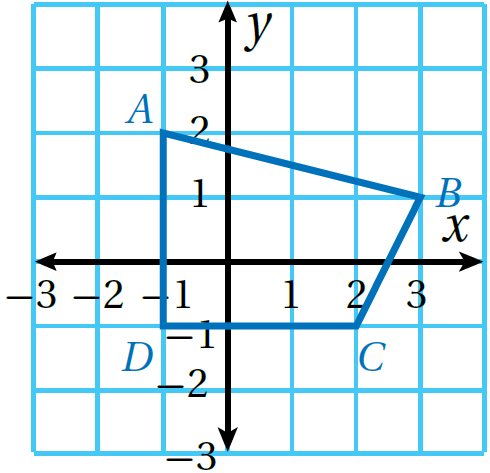
1) أرسمُ المضلعَ ABCD الّذي إحداثياتُ رؤوسِهِ في المستوى . الإحداثيِّ، ثمَّ أرسمُ صورتَهُ تحتَ تأثيرِ تكبيرٍ مركزُهُ نقطةُ الأصلِ وَمُعامِلُهُ 3
الْخُطْوَةُ 1: أرسمُ المضلعَ ABCD في المستوى الإحداثيِّ
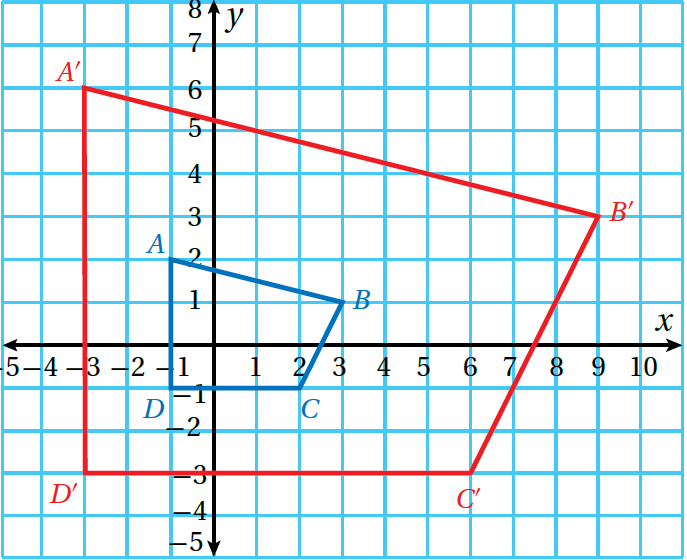
الْخُطْوَةُ 2:أَجِدُ إحداثياتِ رؤوسِ الصورةِ بِضربِ الإحداثيِّ x وَالإحداثيِّ y لِكلِّ رأسٍ مِنْ رؤوسِ الشكلِ الأصليِّ في 3
| إحداثياتُ الصورةِ | إحداثياتُ رؤوسِ الشكلِ الأصليِّ | |
| (3x, 3y) | (x, y) | |
| A'(-3, 6) | A(-1, 2) | |
| B'(9, 3) | B(3, 1) | |
| C'(6, -3) | C(2, -1) | |
| D'(-3, -3) | D(-1, -1) |
الْخُطْوَةُ 3: أرسمُ المضلعَ 'A'B'C'D في المستوى الإحداثيِّ.
بِما أنَّ الشكلَ وَصورتَهُ الناتجةَ عَنْ تكبيرٍ مركزُهُ نقطةُ الأصلِ وَمعامِلُهُ k متشابهانِ، فإنَّهُ يمكنُ إيجادُ معاملِ التكبيرِ k بِإيجادِ النسبةِ بينَ أطوالِ الأضلاعِ المتناظرةِ، أَوْ بِإيجادِ النسبةِ بينَ الإحداثيِّ x أَوِ الإحداثيِّ y لِاحدِ رؤوسِ الشكلِ بعدَ التكبيرِ وَالإحداثيِّ المناظرِ لَهُ في الشكلِ الأصليِّ.
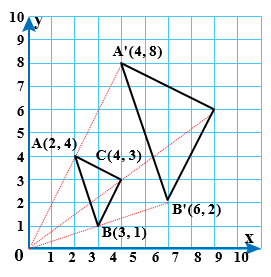
مثال4: يبيّنُ الشكلُ المجاورُ المثلثَ ΔOAB وَصورتَهُ ΔOCD الناتجةَ عَنْ تكبيرٍ مركزُهُ نقطةُ الأصلِ:
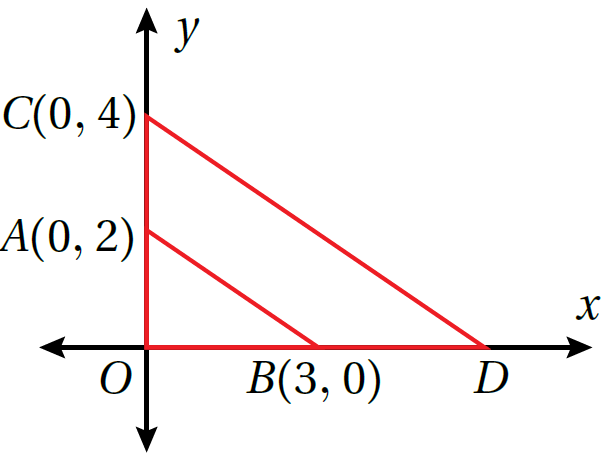
1)أَجِدُ معاملَ التكبيرِ.
الطريقةُ 1: بِما أنَّ ΔOAB ~ ΔOCD فَإنَّ النسبةَ بينَ طولَيْ أيِّ ضلعَينِ متناظرَينِ تساوي معاملَ التكبيرِ: إذنْ، معاملُ التكبيرِ 2
الطريقةُ 2: أَجِدُ النسبةَ بينَ الإحداثيِّ y لِلرأسِ C وَالإحداثيِّ y لِلرأسِ A المناظرِ لَهُ: إذنْ، معاملُ التكبيرِ يساوي 2
2)أَجِدُ إحداثيَّيِ الرأسِ D
المناظرِ لَهُ في معاملِ التكبيرِ B عَنْ ضربِ إحداثيَّيِ الرأسِ D ينتجُ إحداثيّا الرأسِ
إذنْ، D(6,0)
مثال 4: منَ الحياةِ عدساتٌ: تُظهرُ العدسةُ المكبِّرةُ المجاورةُ الأجسامَ أكبرَ بِ 5 مراتٍ مِنْ حجمِها الأصليِّ. إذا كانَ طولُ الدُّعسوقةِ المجاورةِ تحتَ العدسةِ 3.9cm فَأَجِدُ الطولَ الحقيقيَّ لَها.
3.9 = 5× l الطولُ الحقيقيُّ × طولُ الصورةِ يساوي معاملُ التكبيرِ
0.78 = l أقسمُ طرفَِ المعادلةِ على 5
0.78 cm إذنْ، الطولُ الحقيقيُّ لِلدُّعسوقةِ