رياضيات أدبي فصل أول

حلول أسئلة كتاب الطالب وكتاب التمارين 

أسئلة أتحقق من فهمي 

أتحقق من فهمي صفحة 53

أجد قيمة كلٍّ ممّا يأتي :

           $\mathit{a}\mathbf{)} ({}_{13}C_5) - ({}_{8}C_8) \mathbf{ }\mathit{b}\mathbf{)} \left({}_{7}C_0\right)\times \left({}_{7}C_7\right)$

الحل : 

$\mathit{a}\mathbf{)} ({}_{13}C_5) - ({}_{8}C_8) = \frac{13!}{5!(13-5)!} - \frac{8!}{8!(8-8)!} = 1287 -1 = 1286$

 

$\mathit{b}\mathbf{)} ({}_{7}C_0)\times ({}_{7}C_7) =\frac{7!}{0! (7-0)!}\times \frac{7!}{7! (7-7)!}= 1$

---

 

أتحقق من فهمي صفحة 54

أجد عدد طرائق اختيار لجنةٍ تُنظِّم عملية دخول طالبات مدرسة ، تضم 3 طالبات من بين 10 طالبات تطوَّعْنَ لأداء هذه المهمة.

الحل : 

 لإيجاد عدد طرائق اختيار 3 طالبات من بين 10 طالبات تطوعن لأداء هذه المهمة مع عدم أهمية الترتيب أستخدم التوافيق على النحو الآتي :

تعريف التوافيق   : ${}_{10}C_3=\frac{10!}{3! (10-3)!}$

الناتج :                                   $=120$    

---

 

أتحقق من فهمي صفحة 55

مثال 3 : يحتوي صندوق على 5 كرات حمراء مُرقَّمة من ( 5 - 1) ، و 4 كرات زرقاء مُرقَّمة من ( 4 - 1) جميعها مُتماثِلة :

مُعتمِدًا المثال 3، أجد ما يأتي :

a) عدد الطرائق المُمكِنة لسحب كرتين زرقاوين عشوائيًّا من الصندوق إذا سُحِبتا معًا.
b) عدد الطرائق المُمكِنة لسحب كرتين زرقاوين وكرة واحدة حمراء عشوائيًّا من الصندوق إذا كان السحب على التوالي من دون إرجاع.

الحل : 

a) عدد الطرائق المُمكِنة لسحب كرتين زرقاوين عشوائيًّا من الصندوق إذا سُحِبتا معًا.

أفرض أنَّ n(A)  عدد الطرائق التي يُمكن بها سحب كرتين زرقاوين  ، علمًا بأنّ العدد الكلي للكرات الزرقاء في الصندوق 4 كرات، وترتيب سحب الكرات ليس مهمًّا : 

عدد طرائق سحب عنصرين من بين 4 عناصر	$n\left(A\right) = {}_{4}C_2$
بالتعويض في قانون التوافيق	${}_{4}C_2 = \frac{ 4! }{4! (4-2) !}$
الناتج	$= 6$

 

 

 

 

 

---

b) عدد الطرائق المُمكِنة لسحب كرتين زرقاوين وكرة واحدة حمراء عشوائيًّا من الصندوق إذا كان السحب على التوالي من دون إرجاع.

أفترض أنَّ n(B)  عدد الطرائق التي يُمكِن بها سحب كرتين حمراوين وكرة زرقاء.
أُلاحِظ أنَّ الترتيب مهم في هذه المسألة. فمثلًا ، سحب الكرات (زرقاء 1، زرقاء 2، حمراء 3) يختلف عن سحب الكرات (زرقاء 1، حمراء 3، زرقاء 2)، (حمراء 3، زرقاء 1، زرقاء2) ، .... 
أُلاحظ أيضًا أنّ العدد الكلي للكرات الحمراء في الصندوق 5 كرات، وأنَّ العدد الكلي للكرات الزرقاء في الصندوق 4 كرات : 

اختيار عنصرين من بين 4 عناصر، واختيار عنصر واحد من بين 5 عناصر	$n\left(B\right) = {}_{4}P_2 \times {}_{5}P_1$
بالتعويض في قانون التباديل	$= \frac{4!}{(4-2)!} \times \frac{5!}{(5-1)!}$
بالتبسيط	$= 12 \times 5$
الناتج	$= 60$

 

 

 

 

 

 

---

 

 

أسئلة أتدرب وأحل المسائل 

أجد ناتج كلٍّ ممّا يأتي من دون استعمال الآلة الحاسبة : 

$\mathbf{1}\mathbf{)}{}_{10}C_7 \mathbf{ }\mathbf{2}\mathbf{)} {}_{9}C_0 \mathbf{3}\mathbf{)}{}_{7}C_1 +{}_{6}C_3$

الحل : 

$\mathbf{1}\mathbf{)}{}_{10}C_7 = \frac{10!}{7! (10-7)!} = \frac{10\times 9\times 8\times \cancel{7!}}{\cancel{7!}\times 3!} = \mathbf{120}\mathbf{ }\mathbf{ }$

$\mathbf{2}\mathbf{)} {}_{9}C_0 = \frac{9!}{0! (9-0)!}= \mathbf{1}$

$\mathbf{3}\mathbf{)}\mathbf{ }{}_{7}C_1 +{}_{6}C_3 = \frac{7!}{1! (7-1)!} +\frac{6!}{3! (6-3)!} = 7 + 20 =\mathbf{ }\mathbf{27}\mathbf{ }$

 

 

 

 

 

 

 

 

 

---

 

أجد ناتج كلٍّ ممّا يأتي باستعمال الآلة الحاسبة :

$\mathbf{4}\mathbf{)} ({}_{12}C_5)\times ({}_{5}C_3) \mathbf{5}\mathbf{)} \frac{{}_{10}C_6 }{ {}_{8}C_5 } \mathbf{ }\mathbf{6}\mathbf{)} \frac{ {}_{9}C_5}{\left({}_{8}C_5\right)\times \left({}_{3}C_2\right)}$

الحل : 

$\mathbf{4}\mathbf{)} ({}_{12}C_5)\times ({}_{5}C_3) = 792 \times 10 = \mathbf{7920}\mathbf{ }$

$\mathbf{5}\mathbf{)} \frac{{}_{10}C_6 }{ {}_{8}C_5 } = {}_{10}C_6 ÷ {}_{8}C_5 = 210 ÷ 56 =\mathbf{ }\mathbf{3}\mathbf{.}\mathbf{75}\mathbf{ }\mathbf{ }\mathbf{ }\mathbf{ }$

$\mathbf{6}\mathbf{)} \frac{ {}_{9}C_5}{\left({}_{8}C_5\right)\times \left({}_{3}C_2\right)}= \frac{126}{56 \times 3} =\mathbf{ }\mathbf{0}\mathbf{.}\mathbf{75}$

 

 

 

 

 

 

 

 

 

 

---

 

7)  أجد عدد الطرائق المُمكِنة لاختيار نوعي فاكهة من 7 أنواع مختلفة متوافرة في محل لبيع الفواكه.

الحل : 

 لإيجاد عدد طرائق اختيار نوعي فاكهة من 7 أنواع مختلفة مع عدم أهمية الترتيب أستخدم التوافيق : 

    ${}_{7}C_2= \frac{7!}{2! (7-2)!} = \frac{7\times 6\times \cancel{5!} }{ 2!\times \cancel{5!}} = \mathbf{21}\mathbf{ }$

---

  

8) لدى قيس 8 كتب مختلفة، أراد إهداء 3 كتب منها إلى مكتبة المدرسة. أجد عدد الطرائق المُمكِنة لاختيار الكتب التي يرغب قيس في إهدائها.

الحل : 

 لإيجاد عدد طرائق اختيار  3 كتب من بين 8 كتب مختلفة مع عدم أهمية الترتيب أستخدم التوافيق : 

   ${}_{8}C_3= \frac{8!}{3! (8-3)!} = \frac{8\times 7\times 6\times \cancel{5!} }{ 3!\times \cancel{5!}} = \mathbf{56}\mathbf{ }$

---

 

9)  هندسة: أجد عدد المثلثات التي يُمكِن تكوينها من أضلاع الشكل المجاور.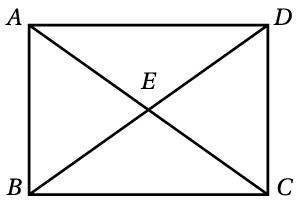

 

 

 

 

 

الحل : 

للشكل المجاور 10 أضلاع مختلفة هي : $AB\hspace{0.17em}, AC , CD , DA , AC , DB , DE , EB ,CE , EA$ ، ويُراد تكوين مثلثات ، عدد أضلاع المثلث 3  ، إذن :  

${}_{10}C_3= \frac{10!}{3! (10-3)!} = \frac{10\times 9\times 8\times \cancel{7!} }{ 3!\times \cancel{7!} } = \mathbf{120}\mathbf{ }$

 

---

 

رياضة : أراد معلِّم التربية الرياضية اختيار طالبينِ من بين 15 طالبًا للمشاركة في المباريات المدرسية:
10) أجد عدد الطرائق المُمكِنة لاختيار هذين الطالبينِ.

الحل : 

عدد طرائق اختيار  طالبين من بين 15 طالب مع عدم أهمية الترتيب أستخدم التوافيق : 

${}_{15}C_2= \frac{15!}{2! (15-2)!} = \frac{15\times 14\times \cancel{13! } }{ 2!\times \cancel{13!}} = \mathbf{105}$

---

11) أجد عدد الطرائق المُمكِنة لاختيار هذين الطالبينِ للمشاركة في المباريات، علمًا بأنَّ الأول سيشارك في مبارة كرة
القدم ، والثاني سيشارك في مباراة كرة السلَّة.

الحل : 

عدد طرائق اختيار  طالبين من بين 15 طالب مع أهمية الترتيب أستخدم التباديل : 

${}_{15}P_2= \frac{15!}{ (15-2)!} = \frac{15\times 14\times \cancel{13!}}{\cancel{13!}} = \mathbf{210}$

---

 

12) هدايا : أرادت إيمان شراء باقة ورد لأمها من أحد محالِّ بيع الورد. بكم طريقة يُمكِن لإيمان شراء باقة فيها 5 وردات
من بين 9 وردات ألوانها مختلفة؟

الحل : 

عدد طرائق اختيار  5 وردات من بين 9 وردات مع عدم أهمية الترتيب أستخدم التوافيق : 

${}_{9}C_5= \frac{9!}{5! (9-5)!} = \frac{9\times 8\times 7\times 6\times \cancel{5! } }{\cancel{ 5!}\times 4! } = \mathbf{126}$

---

13) أجد عدد الطرائق المُمكِنة التي يريد بها سمير شراء 4 أقلام من بين 10 أقلام مختلفة.

الحل : 

عدد طرائق اختيار  4 أقلام من بين 10 أقلام مع عدم أهمية الترتيب أستخدم التوافيق : 

${}_{10}C_4= \frac{10!}{4! (10-4)!} = \frac{10\times 9\times 8\times 7\times \cancel{6!} }{ 4!\times \cancel{6!} } = \mathbf{210}$

---

14)  أكتشف الخطأ: وجد كلٌّ من سعيد وهمام عدد الطرائق المُمكِنة لاختيار 3 طلبة في الصف من بين 11 طالبًا للمشاركة في مشروع تصميم مُخطَّط هندسي لمدرستهم. أيُّهما إجابته صحيحة؟

إجابة سعيد هي الصحيحة لأنّ ترتيب الطلبة غير مهم .

---

15) تبرير : هل يُمكِن أنْ يكون ${}_{n }P_r = {}_{n}C_r$   ، حيث n , r عددان صحيحان موجبان ، و  r ≤ n ؟ أُبرِّر إجابتي.

أفترض أنهما متساويان ، وأجد متى يتحقق ذلك	${}_{n}P_r = {}_{n}C_r$
تعريف التباديل وتعريف التوافيق	$\frac{n!}{(n-r)!} = \frac{n!}{r! (n-r)!}$
بالضرب التبادلي	$n!\times r! (n-r)! = n! (n-r)!$
بالاختصار	$\cancel{n! }\times r! \cancel{(n-r)!} =\cancel{ n!} \cancel{(n-r)!}$
بحل المعادلة الناتجة ، مضروب r يساوي 1 في حالتين عندما  r = 1  أو r = 0	$r! = 1 \Rightarrow \mathbf{ }\mathit{r}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{1}\mathbf{ }\mathbf{,}\mathbf{ }\mathbf{ }\mathit{r}\mathbf{ }\mathbf{=}\mathbf{ }\mathbf{0}$

  

 

 

 

 

 

 

 

 

إذن يُمكن أن يكون ${}_{n }P_r = {}_{n}C_r$ بجالتين عندما تكون r = 1  أو r = 0 

 

---

 

16) تحدٍّ : إذا كان ${}_{10}C_7 = {}_{10}C_3$ ، فأجد صيغة عامة لهذه العلاقة.

الحل : 

أُعمّم الطرف الأيسر  وأستنتج تعميم الطرف الأيمن	${}_{10}C_7 = {}_{10}C_3$
بفرض n = 10  ،  r =  7   إذن : $3 = n - r$	${}_{n}C_r = {}_{n}C_3$
الصيغة العامة للعلاقة	${}_{n}C_r = {}_{n}C_{n-r}$

 

 

 

 

 

---

 

أسئلة كتاب التمارين

أجد قيمة كلٍّ ممّا يأتي من دون استعمال الآلة الحاسبة :

$\mathbf{1}\mathbf{)}{}_{9}C_5 \mathbf{ }\mathbf{2}\mathbf{)} ({}_{10}C_6 )-({}_{9}C_7 )$

الحل : 

$\mathbf{1}\mathbf{)}{}_{9}C_5 = \frac{9!}{5! (9-5)!} = \frac{ 9\times 8\times 7\times 6\times \cancel{5!} }{\cancel{5!} \times 4! } = \mathbf{126}\mathbf{ }$

$\mathbf{2}\mathbf{)} ({}_{10}C_6 )-({}_{9}C_7 ) = \frac{10!}{6!(10-6)!} -\frac{9!}{7!(9-7)!}= 210 -36 =\mathbf{ }\mathbf{174}$

 

 

 

 

 

 

 

 

---

 

أجد قيمة كلٍّ ممّا يأتي باستعمال الآلة الحاسبة:

$\mathbf{3}\mathbf{)} ({}_{15}C_2) ({}_{8}C_3) \mathbf{4}\mathbf{)} \frac{ {}_{12}C_3 }{ {}_{11}C_3 }$

الحل : 

$\mathbf{3}\mathbf{)} ({}_{15}C_2) ({}_{8}C_3)=\frac{15!}{2!(15-2)! }\times \frac{8!}{3!(8-3)! } = 105\times 56 =\mathbf{5880}\mathbf{ }\mathbf{ }$

$$\begin{gathered} \mathbf{4}\mathbf{)} \frac{ {}_{12}C_3 }{ {}_{11}C_3 } =\frac{12!}{3!(12-3)!}÷\frac{11!}{3!(11-3)!} = 220 ÷165 \approx \mathbf{1}\mathbf{.}\mathbf{3}\mathbf{ }\mathbf{ } \\ \mathbf{ } \end{gathered}$$

 

 

 

 

 

 

 

 

---

5) كم لجنة تضم 3 أشخاص يُمكِن تكوينها عشوائيًّا من بين 8 أشخاص؟

الحل : 

$\mathbf{ }{}_{8}C_3 = \frac{8!}{3! (8-3)!} = \frac{ 8\times 7\times 6\times \cancel{5!} }{3!\times \cancel{5!} } = \mathbf{56}\mathbf{ }$

---

6) أجد عدد الطرائق المُمكِنة لتكوين لجنة تضم 2 من المُعلِّمين و 4 من الطلبة الذين اختيروا عشوائيًّا من بين 7 مُعلِّمين وَ 9 طلبة.

الحل : 

عدد الطرائق الممكنة لتكوين لجنة = عدد طرائق اختيار مُعلمَين من بين 7 مُعلمِين $\times$عدد طرائق اختيار 4 طلاب من بين 9 طلبة 

إذن : 

    ${}_{7 }C_2 \times {}_{9}C_4 =\frac{7!}{2!(7-2)! }\times \frac{9!}{4!(9-4)! }=21\times 126= \mathbf{2646}\mathbf{ }$

---

 

7) كم مجموعة جزئية من رقمين يُمكِن تكوينها من الأرقام : 5 , 4 , 3 , 2 , 1؟

الحل : 

المطلوب تكوين مجموعات جزئية ، كل مجموعة تتكون من رقمين ، إذن لا فرق بين المجموعة {1 , 2} , والمجموعة  {2 , 1} ؛ لذا أستخدم التوافيق : 

${}_{5}C_2 = \frac{5!}{2! (5-2)!} = \frac{5\times 4\times \cancel{3!} }{2! \times \cancel{ 3!}} =\mathbf{ }\mathbf{10}$

---

8) أجد عدد الطرائق التي يُمكِن بها لطبيب اختيار نوعين من الضمادات الطبية من بين 9 أنواع مختلفة متوافرة لديه.

الحل : 

${}_{9}C_2= \frac{9!}{2! (9-2)!} = \frac{9\times 8\times \cancel{7!} }{2! \times \cancel{ 7!}} =\mathbf{ }\mathbf{36}$

---

 

يراد اختيار 4 طلاب عشوائيًّا من صف فيه 22 طالبًا؛ للمشاركة في مسابقات تُنظِّمها المدرسة :
9) أجد عدد الطرائق المُمكِنة لاختيار هؤلاء الطلاب.

الحل : 

ترتيب الطلبة غير مهم هنا ، لذا أستخدم التوافيق :

${}_{22}C_4= \frac{22!}{4! (22-4)!} = \frac{22\times 21\times 20\times 19\times \cancel{18!} }{4! \times \cancel{ 18!}} =\mathbf{ }\mathbf{7315}$

10) أجد عدد الطرائق المُمكِنة لاختيار هؤلاء الطلاب إذا كان الأول سيشارك في مسابقة الشِّعر، والثاني سيشارك في مسابقة
الرياضيات، والثالث سيشارك في مسابقة الثقافة العامة، والرابع سيشارك في مسابقة مهارات الحاسوب.

الحل : 

ترتيب الطلبة مهم هنا ، لذا أستخدم التباديل : 

${}_{22}P_4= \frac{22!}{ (22-4)!} = \frac{22\times 21\times 20\times 19\times \cancel{18!} }{ \cancel{ 18!}} =\mathbf{ }\mathbf{175560}$

---

11) ذهب سعيد إلى محل لبيع الملابس، فوجد فيه 9 ألوان مختلفة من القمصان، و 8 ألوان مختلفة من البناطيل. أجد عدد
الطرائق المختلفة التي يُمكِن بها لسعيد شراء 3 قمصان و 4 بناطيل من هذا المحل.

الحل : 

عدد الطرائق التي يُمكن لسعيد شراء 3 قمصان و 4 بناطيل = عدد طرائق اختيار 3 قمصان من بين 9 قمصان $\times$ عدد طرائق اختيار 4 طلاب من بين 8 بناطيل ، إذن : 

${}_{9 }C_3 \times {}_{8}C_4 =\frac{9!}{3!(9-3)! }\times \frac{8!}{4!(8-4)! }=84\times 70= \mathbf{5880}\mathbf{ }$

---

12) أجد عدد الطرائق المختلفة التي يُمكِن بها اختيار كتابين من 5 كتب ثقافية و 3 كتب من 5 كتب تاريخية.

الحل : 

 ${}_{5 }C_2 \times {}_{5}C_3 =\frac{5!}{2!(5-2)! }\times \frac{5!}{3!(5-3)! }=10\times 10= \mathbf{100}\mathbf{ }$

---