رياضيات فصل ثاني

فكرة الدرس: أستعمل الخصائص: التبديلية، والتجميعية، والتوزيعية؛ لتبسيط مقادير جبرية.

 

المُصطلحات: المقدار الجبري، الخاصية التبديلية، الخاصية التجميعية، خاصية التوزيع.

 

المقدار الجبري : هو عبارة تحتوي مُتغيرات وأعدادًا تفصل بينها عمليات.

فمثلًا ، المقدار الجبري m + 5   يُمثل مجموع قيمة مجهولة (مُتغير) مع العدد 5 ، ويُمكن استعمال أي حرف للتعبير عن القيمة المجهولة.

الحرفx   هو الأكثر استعمالًا بوصفه مُتغيرًا، ولتجنب الخلط بين الحرفx   ورمز عملية الضرب  ، تُستعمل طرائق مُتعددة للتعبير عن عملية الضرب.

 

◘ يُمكن استبدال المتغيرات في مقدار جبري بأعداد، وعندئذ يُمكن إيجاد قيمة للمقدار الجبري باتباع أولويات العمليات.

مثال 

أجد قيمة كل مقدار جبري مما يأتي إذا كانت  a = 2     ,    b =  -4   ,   c = 0.3

الحل: 

$$\begin{gathered} \mathbf{1}\mathbf{)} 9+a^2=9+2^2 \\ =9+4=13 \end{gathered}$$

$$\begin{gathered} \mathbf{2}\mathbf{)}\mathbf{ }\frac{6b}{2.7+c}=\frac{6(-4)}{2.7+0.3} \\ =\frac{-24}{3}=-8 \end{gathered}$$

$$\begin{gathered} \mathbf{3}\mathbf{)} 2c-b^3+(7a+1) =2(0.3)-{(-4)}^3+(7\left(2\right)+1) \\ =0.6-(-64)+15 \\ =79.6 \end{gathered}$$

 

 

 

 

 

 

 

 

 

 

 

---

◘ يُمكن استعمال الخاصية التبديلية، والخاصية التجميعية لتبسيط مقادير جبرية.

مفهوم أساسي (الخاصّيتان: التبديلية، والتّجميعيّة)

الخاصية التبديلية

بالكلمات : لا يتغير ناتج جمع عددين أو ضربهما بتغير ترتيبهما.

أمثلة:	بالأعداد	بالرموز
	$5+3=3+5$	$a+b=b+a$
	$2\times 7=7\times 2$	$a\times b=b\times a$

 

 

 

 

الخاصية التجميعية

بالكلمات : لا يتغير مجموع ثلاثة أعداد، أو ناتج ضربها بتغير العددين اللذين أبدأ بهما.

أمثلة:	بالأعداد	بالرموز
	$4+(6+1)=(4+6)+1$	$a+(b+c)=(a+b)+c$
	$9\times (2\times 5)=(9\times 2)\times 5$	$a\times (b\times c)=(a\times b)\times c$

 

 

 

 

مثال  

أبسط كل مقدار جبري في كل مما يأتي:

 

الخاصية التبديلية للجمع	$\mathbf{1}\mathbf{)} 8+(g+3)=8+(3+g)$
الخاصية التجميعية للجمع	$=(8+3)+g$
نجمع	$=11+g$
الخاصية التبديلية للجمع	$\mathbf{2}\mathbf{)}\mathbf{ }12+(n+2.5)=12+(2.5+n)$
الخاصية التجميعية للجمع	$=(12+2.5)+n$
نجمع	$=14.5+n$
الخاصية التجميعية للضرب	$\mathbf{3}\mathbf{)} 4(9W)=(4\times 9)W$
نضرب	$=36W$

 

 

 

 

 

 

 

 

 

 

 

 

---

◘ يُمكن أيضا استعمال خاصية التوزيع لتبسيط مقادير جبرية.

مفهوم اساسي (خاصية التوزيع)

بالكلمات: لضرب عدد في مجموع عددين أو الفرق بينهما ، أضرب كل عدد بين القوسين بالعدد الذي خارجهما.

بالأعداد	بالرموز

 

 

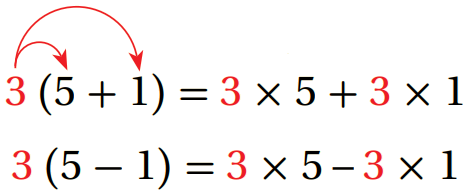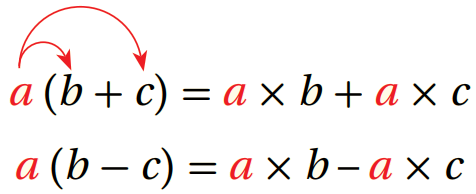مثال

أستعمل خاصية التوزيع لتبسيط كل مقدار جبري في كل مما يأتي:

خاصية التوزيع	$\mathbf{1}\mathbf{)} 3(m + 2)=3\times m+3\times 2$
نضرب	$=3m+6$
خاصية التوزيع	$\mathbf{2}\mathbf{)} 6(k – 4)=6\times k-6\times 4$
نضرب	$=6k-24$
خاصية التوزيع	$\mathbf{3}\mathbf{)} 5(7y – 8)=5\times 7y-5\times 8$
نضرب	$=35y-40$

 

 

 

 

 

 

 

 

 

 

 

 

مثال

تذكرة الدخول إلى مدينة ألعاب 2.5 دينار، ويُستوفى مبلغ مقداره 0.5 دينار عن كل لعبة يستخدمها الشخص:

1) أكتب مقدارًا جبريًا يُمثل التكلفة إذا استخدم الشخص عددًا من الألعاب.

2) ما التكلفة التي سيدفعها شخص لعب 10 مرات.    

الحل:

1) بالكلمات: تكلفة الدخول 2.5 دينار، وثمن اللعبة الواحدة 0.5 دينار، وعدد مرات اللعب مجهول.

بالرموز: تكلفة الدخول 2.5 دينار، وثمن اللعبة الواحدة 0.5 دينار، وعدد مرات اللعب m.

المقدار الجبري: $2.5+0.5\times m$، ويُمكن كتابته أيضا: $2.5+0.5m$ 

 

2) لإيجاد التكلفة عوضm = 10   في المقدار الجبري

$2.5+0.5m$	نكتب المقدار الجبري
$=2.5+0.5\times 10$	نعوض m=10
$=2.5+5=7.5$	نضرب ثم نجمع

 

 

 

 

 

إذن؛ التكلفة التي سيدفعها شخص لعب 10 مرات تُساوي 7.5 دينار.